《python深度学习》学习笔记与代码实现（第三章）

第三章 神经网络入门

1.神经网络剖析
1.1 层：深度学习的基础部件
5层神经网络，8层神经网络，等等

1.2 模型：层构成的网络
深度学习的模型时层构成的有向无环图。最常见的例子就是层的线性堆叠，将单一输入映射为单一输出

1.3 损失函数与优化器：配置学习过程的关键
损失函数：在训练过程中需要将其最小化，它能够衡量当前任务是否已经完成
优化器：决定如何基于损失函数对网络进行更新，它执行的是随机梯度下降的某个变体

2.电影评论分类：二分类问题
二元分类，或者称为二值分类，可能是应用最广泛的机器学习问题。通过学习本例，你将掌握如何基于文本内容将影评分为正、负二类。

本文将从互联网电影数据库（IMDB）获取50,000个流行电影影评作为数据集。这里将其分割为25,000个影评的训练集和25,000个影评的测试集。其中每个数据集都包含50%的好评和50%的差评。

# 导入数据
from keras.datasets 
import imdb(train_data,train_labels),(test_data,test_labels) = imdb.load_data(num_words = 10000)
# 查看这两个数据
train_data[0]train_labels[0]
# 最长的句子只有10000个单词
max([max(sequence) for sequence in train_data])

word_index = imdb.get_word_index()
reverse_word_index = dict([(value,key) for (key,value) in word_index.items()])
decoded_review = ''.join([reverse_word_index.get(i-3,'?') for i in train_data[0]])
# print(decoded_review)

?thisfilmwasjustbrilliantcastinglocationscenerystorydirectioneveryone'sreallysuitedtheparttheyplayedandyoucouldjustimaginebeingthererobert?isanamazingactorandnowthesamebeingdirector?fathercamefromthesamescottishislandasmyselfsoilovedthefacttherewasarealconnectionwiththisfilmthewittyremarksthroughoutthefilmweregreatitwasjustbrilliantsomuchthatiboughtthefilmassoonasitwasreleasedfor?andwouldrecommendittoeveryonetowatchandtheflyfishingwasamazingreallycriedattheenditwassosadandyouknowwhattheysayifyoucryatafilmitmusthavebeengoodandthisdefinitelywasalso?tothetwolittleboy'sthatplayedthe?ofnormanandpaultheywerejustbrilliantchildrenareoftenleftoutofthe?listithinkbecausethestarsthatplaythemallgrownuparesuchabigprofileforthewholefilmbutthesechildrenareamazingandshouldbepraisedforwhattheyhavedonedon'tyouthinkthewholestorywassolovelybecauseitwastrueandwassomeone'slifeafterallthatwassharedwithusall

import numpy as np
# 将每个句子进行独热编码，形成0，1矩阵
def vectorize_sequences(sequences,dimension = 10000):
    results = np.zeros((len(sequences),dimension))
    for i,sequence in enumerate(sequences):
        results[i,sequence] = 1.
    return results

x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)

# 将标签也进行向量化
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

x_train[0]

array([0., 1., 1., ..., 0., 0., 0.])

from keras import models
from keras import layers

model = models.Sequential()
model.add(layers.Dense(16,activation = 'relu',input_shape = (10000,)))
model.add(layers.Dense(16,activation = 'relu'))
model.add(layers.Dense(1,activation = 'sigmoid'))

# 损失函数为二元交叉熵,三个参数依次为：优化器，损失函数，评价指标
model.compile(optimizer = 'rmsprop',loss = 'binary_crossentropy',metrics = ['acc'])

# 把训练样本分为训练集和交叉测试集
x_val = x_train[:10000]
partial_x_train = x_train[10000:]

y_val = y_train[:10000]
partial_y_train = y_train[10000:]


result = model.fit(partial_x_train,partial_y_train,epochs = 20,batch_size = 512,validation_data = (x_val,y_val))

Train on 15000 samples, validate on 10000 samples
Epoch 1/20
15000/15000 [==============================] - 5s 338us/step - loss: 0.5326 - acc: 0.7917 - val_loss: 0.4064 - val_acc: 0.8700
Epoch 2/20
15000/15000 [==============================] - 4s 235us/step - loss: 0.3258 - acc: 0.8987 - val_loss: 0.3154 - val_acc: 0.8851
Epoch 3/20
15000/15000 [==============================] - 3s 232us/step - loss: 0.2357 - acc: 0.9245 - val_loss: 0.2827 - val_acc: 0.8899
Epoch 4/20
15000/15000 [==============================] - 3s 233us/step - loss: 0.1866 - acc: 0.9397 - val_loss: 0.2862 - val_acc: 0.8838
Epoch 5/20
15000/15000 [==============================] - 4s 235us/step - loss: 0.1502 - acc: 0.9521 - val_loss: 0.2768 - val_acc: 0.8887
Epoch 6/20
15000/15000 [==============================] - 4s 236us/step - loss: 0.1256 - acc: 0.9615 - val_loss: 0.3118 - val_acc: 0.8800
Epoch 7/20
15000/15000 [==============================] - 3s 233us/step - loss: 0.1045 - acc: 0.9687 - val_loss: 0.3120 - val_acc: 0.8837
Epoch 8/20
15000/15000 [==============================] - 4s 234us/step - loss: 0.0882 - acc: 0.9730 - val_loss: 0.3211 - val_acc: 0.8817
Epoch 9/20
15000/15000 [==============================] - 3s 232us/step - loss: 0.0736 - acc: 0.9792 - val_loss: 0.3548 - val_acc: 0.8819
Epoch 10/20
15000/15000 [==============================] - 4s 240us/step - loss: 0.0595 - acc: 0.9851 - val_loss: 0.3971 - val_acc: 0.8744
Epoch 11/20
15000/15000 [==============================] - 4s 236us/step - loss: 0.0508 - acc: 0.9863 - val_loss: 0.3904 - val_acc: 0.8782
Epoch 12/20
15000/15000 [==============================] - 4s 235us/step - loss: 0.0396 - acc: 0.9912 - val_loss: 0.4199 - val_acc: 0.8742
Epoch 13/20
15000/15000 [==============================] - 4s 235us/step - loss: 0.0335 - acc: 0.9933 - val_loss: 0.4490 - val_acc: 0.8725
Epoch 14/20
15000/15000 [==============================] - 4s 244us/step - loss: 0.0278 - acc: 0.9943 - val_loss: 0.4748 - val_acc: 0.8734
Epoch 15/20
15000/15000 [==============================] - 4s 235us/step - loss: 0.0239 - acc: 0.9947 - val_loss: 0.5067 - val_acc: 0.8704
Epoch 16/20
15000/15000 [==============================] - 4s 235us/step - loss: 0.0164 - acc: 0.9979 - val_loss: 0.5940 - val_acc: 0.8555
Epoch 17/20
15000/15000 [==============================] - 4s 234us/step - loss: 0.0124 - acc: 0.9988 - val_loss: 0.5650 - val_acc: 0.8676
Epoch 18/20
15000/15000 [==============================] - 4s 235us/step - loss: 0.0112 - acc: 0.9988 - val_loss: 0.6037 - val_acc: 0.8653
Epoch 19/20
15000/15000 [==============================] - 4s 242us/step - loss: 0.0089 - acc: 0.9992 - val_loss: 0.6369 - val_acc: 0.8646
Epoch 20/20
15000/15000 [==============================] - 4s 253us/step - loss: 0.0078 - acc: 0.9982 - val_loss: 0.6863 - val_acc: 0.8683

# 绘制训练损失和验证损失
import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']

epochs = range(1,len(loss_values) + 1 )

plt.plot(epochs,loss_values,'bo',label = 'Training loss')
plt.plot(epochs,val_loss_values,'b',label = 'Validation loss')

plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()

plt.show()

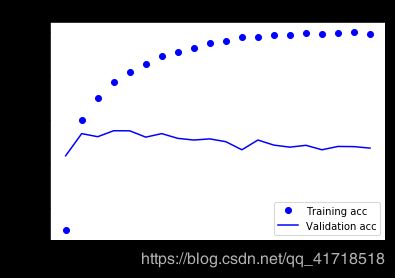
# 绘制训练精度和验证精度
plt.clf() # 清空图像
acc = history_dict['acc']
val_acc = history_dict['val_acc']

plt.plot(epochs,acc,'bo',label = 'Training acc')
plt.plot(epochs,val_acc,'b',label = 'Validation acc')

plt.title('Training and validation acc')
plt.xlabel('Epochs')
plt.ylabel('acc')
plt.legend()

plt.show()

# 重头开始训练一个模型
model = models.Sequential()
model.add(layers.Dense(16,activation = 'relu',input_shape = (10000,)))
model.add(layers.Dense(16,activation = 'relu'))
model.add(layers.Dense(1,activation = 'sigmoid'))

model.compile(optimizer = 'rmsprop',loss = 'binary_crossentropy',metrics = ['accuracy'])

model.fit(x_train,y_train,epochs = 4,batch_size = 512)

results = model.evaluate(x_test,y_test)

print(results)

Epoch 1/4
25000/25000 [==============================] - 12s 478us/step - loss: 0.4383 - acc: 0.8220
Epoch 2/4
25000/25000 [==============================] - 4s 172us/step - loss: 0.2485 - acc: 0.9127
Epoch 3/4
25000/25000 [==============================] - 4s 153us/step - loss: 0.1965 - acc: 0.9304
Epoch 4/4
25000/25000 [==============================] - 4s 147us/step - loss: 0.1659 - acc: 0.9391
25000/25000 [==============================] - 6s 259us/step
[0.30140374687194826, 0.88092]

从本实例学到的知识点：

原始数据集预处理为张量传入神经网络。单词序列编码为二值向量或者其它形式；
一系列带有relu激活函数的Dense layer能解决广泛的问题，包括情感分类，后续会常用到的；
二值分类问题（输出两个类别）中，最后的一个Dense layer带有一个sigmoid激活函数和一个单元：网络输出是0到1之间的标量，代表概率值；
二分类问题中有sigmoid标量输出的，损失函数选择binary_crossentropy损失函数；
rmsprop优化器对于大部分深度学习模型来说是足够好的选择；
随着在训练集上表现越来越好，神经网络模型开始过拟合，在新数据上表现越来越差。关注验证集上的监控指标

3.新闻分类：多分类问题
在本小节，你将学习构建神经网络，把路透社新闻分为互不相交的46类主题。很明显，这个问题是多分类问题，并且每个数据点都只归为一类，那么该问题属于单标签、多分类；如果每个数据点可以属于多个分类，那么你面对的将是多标签、多分类问题。

路透社新闻数据集是由路透社1986年发布的短新闻和对应主题的集合，它常被用作文本分类的练手数据集。该数据集有46个不同的新闻主题，在训练集中每个主题包含至少10个新闻。

from keras.datasets import reuters
(train_data,train_labels),(test_data,test_labels) = reuters.load_data(num_words = 10000)
len(train_data)
train_data[0]

[1,
 2,
 2,
 8,
 43,
 10,
 447,
 5,
 25,
 207,
 270,
 5,
 3095,
 111,
 16,
 369,
 186,
 90,
 67,
 7,
 89,
 5,
 19,
 102,
 6,
 19,
 124,
 15,
 90,
 67,
 84,
 22,
 482,
 26,
 7,
 48,
 4,
 49,
 8,
 864,
 39,
 209,
 154,
 6,
 151,
 6,
 83,
 11,
 15,
 22,
 155,
 11,
 15,
 7,
 48,
 9,
 4579,
 1005,
 504,
 6,
 258,
 6,
 272,
 11,
 15,
 22,
 134,
 44,
 11,
 15,
 16,
 8,
 197,
 1245,
 90,
 67,
 52,
 29,
 209,
 30,
 32,
 132,
 6,
 109,
 15,
 17,
 12]

word_index = reuters.get_word_index()
# 将单词和索引对调位置
reverse_word_index = dict([(value,key) for (key,value) in word_index.items()])
decoded_newswire = ''.join([reverse_word_index.get(i-3,'?') for i in train_data[0]])
decoded_newswire

'???saidasaresultofitsdecemberacquisitionofspacecoitexpectsearningspersharein1987of115to130dlrspershareupfrom70ctsin1986thecompanysaidpretaxnetshouldrisetonineto10mlndlrsfromsixmlndlrsin1986andrentaloperationrevenuesto19to22mlndlrsfrom125mlndlrsitsaidcashflowpersharethisyearshouldbe250tothreedlrsreuter3'

import numpy as np

# 将训练数据向量化,one-hot编码
def vectorize_sequences(sequences,dimension = 10000):
    results = np.zeros((len(sequences),dimension))
    for i,sequence in enumerate(sequences):
        results[i,sequence] = 1
    return results

x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)

# 对标签也进行向量化，因为有46个标签，所以进行one-hot编码
def to_one_hot(labels,dimension = 46):
    results = np.zeros((len(labels),dimension))
    for i,label in enumerate(labels):
        results[i,label] = 1
    return results

one_hot_train_labels = to_one_hot(train_labels)
one_hot_test_labels = to_one_hot(test_labels)
print(one_hot_train_labels[0])

# 注意，keras可以用内置的方法实现这个操作
from keras.utils.np_utils import to_categorical
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)
print(one_hot_train_labels[0])

[0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

# 开始构建网络
from keras import models
from keras import layers

model = models.Sequential()
model.add(layers.Dense(64,activation = 'relu',input_shape = (10000,)))
model.add(layers.Dense(64,activation = 'relu'))
model.add(layers.Dense(46,activation = 'softmax'))

# 指定损失函数的类型，优化器类型等
model.compile(optimizer = 'rmsprop',loss = 'categorical_crossentropy',metrics = ['accuracy'])

# 将数据分为训练集和交叉验证集
x_val = x_train[:1000]
partial_x_train = x_train[1000:]

y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]

# 训练模型
history = model.fit(partial_x_train,partial_y_train,epochs = 20,batch_size = 512,validation_data = (x_val,y_val))

Train on 7982 samples, validate on 1000 samples
Epoch 1/20
7982/7982 [==============================] - 19s 2ms/step - loss: 2.5507 - acc: 0.5291 - val_loss: 1.6875 - val_acc: 0.6250
Epoch 2/20
7982/7982 [==============================] - 1s 148us/step - loss: 1.4181 - acc: 0.6984 - val_loss: 1.2969 - val_acc: 0.7210
Epoch 3/20
7982/7982 [==============================] - 1s 152us/step - loss: 1.0661 - acc: 0.7755 - val_loss: 1.1533 - val_acc: 0.7480
Epoch 4/20
7982/7982 [==============================] - 1s 156us/step - loss: 0.8420 - acc: 0.8247 - val_loss: 1.0469 - val_acc: 0.7700
Epoch 5/20
7982/7982 [==============================] - 1s 151us/step - loss: 0.6770 - acc: 0.8554 - val_loss: 0.9674 - val_acc: 0.7950
Epoch 6/20
7982/7982 [==============================] - 1s 151us/step - loss: 0.5370 - acc: 0.8861 - val_loss: 0.9304 - val_acc: 0.7940
Epoch 7/20
7982/7982 [==============================] - 1s 153us/step - loss: 0.4330 - acc: 0.9078 - val_loss: 0.8959 - val_acc: 0.8050
Epoch 8/20
7982/7982 [==============================] - 1s 152us/step - loss: 0.3485 - acc: 0.9267 - val_loss: 0.8999 - val_acc: 0.8060
Epoch 9/20
7982/7982 [==============================] - 1s 153us/step - loss: 0.2943 - acc: 0.9354 - val_loss: 0.8915 - val_acc: 0.8090
Epoch 10/20
7982/7982 [==============================] - 1s 153us/step - loss: 0.2422 - acc: 0.9440 - val_loss: 0.8716 - val_acc: 0.8240
Epoch 11/20
7982/7982 [==============================] - 1s 152us/step - loss: 0.2070 - acc: 0.9501 - val_loss: 0.8944 - val_acc: 0.8060
Epoch 12/20
7982/7982 [==============================] - 1s 150us/step - loss: 0.1906 - acc: 0.9496 - val_loss: 0.9115 - val_acc: 0.8080
Epoch 13/20
7982/7982 [==============================] - 1s 151us/step - loss: 0.1652 - acc: 0.9531 - val_loss: 0.9392 - val_acc: 0.8060
Epoch 14/20
7982/7982 [==============================] - 1s 151us/step - loss: 0.1525 - acc: 0.9543 - val_loss: 1.0099 - val_acc: 0.7890
Epoch 15/20
7982/7982 [==============================] - 1s 154us/step - loss: 0.1425 - acc: 0.9543 - val_loss: 0.9689 - val_acc: 0.8070
Epoch 16/20
7982/7982 [==============================] - 1s 153us/step - loss: 0.1294 - acc: 0.9559 - val_loss: 0.9896 - val_acc: 0.8080
Epoch 17/20
7982/7982 [==============================] - 1s 158us/step - loss: 0.1215 - acc: 0.9579 - val_loss: 1.0397 - val_acc: 0.7910
Epoch 18/20
7982/7982 [==============================] - 1s 154us/step - loss: 0.1196 - acc: 0.9593 - val_loss: 0.9960 - val_acc: 0.8120
Epoch 19/20
7982/7982 [==============================] - 1s 148us/step - loss: 0.1192 - acc: 0.9559 - val_loss: 0.9938 - val_acc: 0.8130
Epoch 20/20
7982/7982 [==============================] - 1s 151us/step - loss: 0.1095 - acc: 0.9575 - val_loss: 1.0413 - val_acc: 0.7990

import matplotlib.pyplot as plt

loss = history.history['loss']
val_loss = history.history['val_loss']



def drawLossAndAcc(x,y1,y2,titles = ''):
    plt.plot(x,y1,'bo',label = 'Train Loss or Accuracy')
    plt.plot(x,y2,'b',label = 'Validation Loss or Accuracy')
    
    plt.title(titles)
    plt.xlabel('Epochs')
    plt.ylabel('Loss or Accuracy')
    plt.legend()
    plt.show()
    
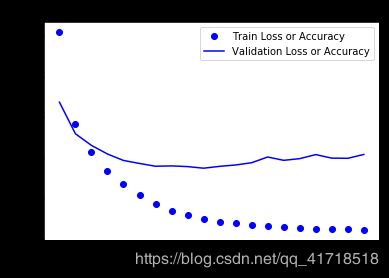
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1,len(loss)+1)
drawLossAndAcc(epochs,loss,val_loss,'Loss')

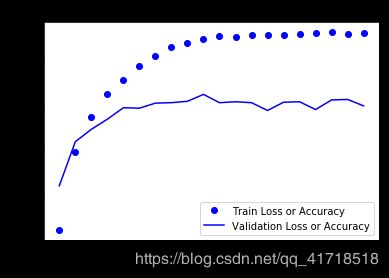
acc = history.history['acc']
val_acc = history.history['val_acc']
epochs = range(1,len(acc)+1)
drawLossAndAcc(epochs,acc,val_acc,'Accuracy')

# 在第九次左右出现过拟合，重新训练一个网络，让他只迭代9次
model = models.Sequential()
model.add(layers.Dense(64,activation = 'relu',input_shape = (10000,)))
model.add(layers.Dense(64,activation = 'relu'))
model.add(layers.Dense(46,activation = 'softmax'))

# 指定损失函数的类型，优化器类型等
model.compile(optimizer = 'rmsprop',loss = 'categorical_crossentropy',metrics = ['accuracy'])
history = model.fit(partial_x_train,partial_y_train,epochs = 8,batch_size = 512,validation_data = (x_val,y_val))
results = model.evaluate(x_test,one_hot_test_labels)
print(results)

Train on 7982 samples, validate on 1000 samples
Epoch 1/8
7982/7982 [==============================] - 1s 177us/step - loss: 2.5043 - acc: 0.5459 - val_loss: 1.7318 - val_acc: 0.6320
Epoch 2/8
7982/7982 [==============================] - 1s 152us/step - loss: 1.3879 - acc: 0.7038 - val_loss: 1.2876 - val_acc: 0.7170
Epoch 3/8
7982/7982 [==============================] - 1s 150us/step - loss: 1.0521 - acc: 0.7712 - val_loss: 1.1364 - val_acc: 0.7540
Epoch 4/8
7982/7982 [==============================] - 1s 151us/step - loss: 0.8371 - acc: 0.8216 - val_loss: 1.0412 - val_acc: 0.7950
Epoch 5/8
7982/7982 [==============================] - 1s 150us/step - loss: 0.6724 - acc: 0.8596 - val_loss: 0.9815 - val_acc: 0.7930
Epoch 6/8
7982/7982 [==============================] - 1s 153us/step - loss: 0.5395 - acc: 0.8890 - val_loss: 0.9516 - val_acc: 0.7920
Epoch 7/8
7982/7982 [==============================] - 1s 152us/step - loss: 0.4396 - acc: 0.9083 - val_loss: 0.9023 - val_acc: 0.8110
Epoch 8/8
7982/7982 [==============================] - 1s 150us/step - loss: 0.3548 - acc: 0.9246 - val_loss: 0.8841 - val_acc: 0.8140
2246/2246 [==============================] - 0s 218us/step
[0.9657114454389999, 0.7845057880676759]

# 在新数据上生成测试结果
predictions = model.predict(x_test)
print('预测结果的大小:',predictions[0].shape)
print('列向量之和:',np.sum(predictions[0]))
print('最大元素的位置（类别）：',np.argmax(predictions[0]))

# 处理标签的另一种方法，将其转换为整数张量

# y_train = np.array(train_labels)
# y_test = np.array(test_labels)
# 这样转换时，只需要将损失函数选为sparse_categorical_crossentropy 即可，只是同种方法的不同表示形式

预测结果的大小: (46,)
列向量之和: 1.0000001
最大元素的位置（类别）： 3

# 中间层维度足够大的重要性
# 输出为46个类别，所以我们中间层的神经元数目不能太小
# 增大神经元看结果
# 在第九次左右出现过拟合，重新训练一个网络，让他只迭代9次
model = models.Sequential()
model.add(layers.Dense(128,activation = 'relu',input_shape = (10000,)))
model.add(layers.Dense(128,activation = 'relu'))
model.add(layers.Dense(128,activation = 'relu'))
model.add(layers.Dense(46,activation = 'softmax'))

# 指定损失函数的类型，优化器类型等
model.compile(optimizer = 'rmsprop',loss = 'categorical_crossentropy',metrics = ['accuracy'])
history = model.fit(partial_x_train,partial_y_train,epochs = 9,batch_size = 512,validation_data = (x_val,y_val))
results = model.evaluate(x_test,one_hot_test_labels)
print(results)

Train on 7982 samples, validate on 1000 samples
Epoch 1/9
7982/7982 [==============================] - 2s 201us/step - loss: 2.2824 - acc: 0.5410 - val_loss: 1.4298 - val_acc: 0.6840
Epoch 2/9
7982/7982 [==============================] - 1s 162us/step - loss: 1.1867 - acc: 0.7340 - val_loss: 1.1448 - val_acc: 0.7600
Epoch 3/9
7982/7982 [==============================] - 1s 163us/step - loss: 0.8614 - acc: 0.8089 - val_loss: 1.0324 - val_acc: 0.7670
Epoch 4/9
7982/7982 [==============================] - 1s 161us/step - loss: 0.6364 - acc: 0.8576 - val_loss: 0.9332 - val_acc: 0.8110
Epoch 5/9
7982/7982 [==============================] - 1s 163us/step - loss: 0.4530 - acc: 0.9050 - val_loss: 0.9022 - val_acc: 0.8140
Epoch 6/9
7982/7982 [==============================] - 1s 159us/step - loss: 0.3360 - acc: 0.9270 - val_loss: 0.9570 - val_acc: 0.8050
Epoch 7/9
7982/7982 [==============================] - 1s 163us/step - loss: 0.2608 - acc: 0.9420 - val_loss: 1.0241 - val_acc: 0.7850
Epoch 8/9
7982/7982 [==============================] - 1s 162us/step - loss: 0.2204 - acc: 0.9476 - val_loss: 0.9642 - val_acc: 0.8090
Epoch 9/9
7982/7982 [==============================] - 1s 161us/step - loss: 0.1768 - acc: 0.9528 - val_loss: 1.0295 - val_acc: 0.7900
2246/2246 [==============================] - 1s 226us/step
[1.1476774699753773, 0.780498664345151]
​

从本例应该学习到的知识点：

如果你想将数据分为N类，那神经网络模型最后一个Dense layer大小为N；
在单标签、多分类的问题中，模型输出应该用softmax激活函数，输出N个分类的概率分布；
分类交叉熵是分类问题合适的损失函数。它最小化模型输出的概率分布和真实label的概率分布之间的距离；
处理多分类中label的两种方法：
通过one-hot编码编码label，并使用categorical_crossentropy作为损失函数；
通过整数张量编码label，并使用sparse_categorical_crossentropy损失函数
对于数据分类的类别较多的情况，应该避免创建较小的中间layer，导致信息瓶颈。

4.预测房价：回归问题
前面两个例子都可以看成是分类问题，它的目标是预测某个输入数据点的单个离散label。常见的另外一类机器学习问题是线性回归，其预测的是一个连续值，而不是离散label。比如，根据气象信息预测明天的气温；根据软件项目计划书预测实现时间。

注意：不要混淆线性回归和逻辑回归算法。逻辑回归不是回归算法，而是分类算法。

波士顿房价数据集是1970年代中期波士顿郊区的数据样本，包含犯罪率、不动产税税率等。你将用该数据集预测当地房价的中间价。波士顿房价数据集与前面两个例子都不太一样，数据样本点相当少：只有506个，其中404个作为训练样本和102个测试样本。输入数据的每个特征都有不同的scale。例如，一些比例值，取值范围在0和1之间；另一些取值在1到12之间；还有些取值在0到100之间，等等。

# 波士顿房价预测
from keras.datasets import boston_housing
(train_data,train_target),(test_data,test_target) = boston_housing.load_data()

Using TensorFlow backend.
Downloading data from https://s3.amazonaws.com/keras-datasets/boston_housing.npz
57344/57026 [==============================] - 0s 5us/step

train_data.shape
test_data.shape
train_target

(404, 13)
(102, 13)
array([15.2, 42.3, 50. , 21.1, 17.7, 18.5, 11.3, 15.6, 15.6, 14.4, 12.1,
       17.9, 23.1, 19.9, 15.7,  8.8, 50. , 22.5, 24.1, 27.5, 10.9, 30.8,
       32.9, 24. , 18.5, 13.3, 22.9, 34.7, 16.6, 17.5, 22.3, 16.1, 14.9,
       23.1, 34.9, 25. , 13.9, 13.1, 20.4, 20. , 15.2, 24.7, 22.2, 16.7,
       12.7, 15.6, 18.4, 21. , 30.1, 15.1, 18.7,  9.6, 31.5, 24.8, 19.1,
       22. , 14.5, 11. , 32. , 29.4, 20.3, 24.4, 14.6, 19.5, 14.1, 14.3,
       15.6, 10.5,  6.3, 19.3, 19.3, 13.4, 36.4, 17.8, 13.5, 16.5,  8.3,
       14.3, 16. , 13.4, 28.6, 43.5, 20.2, 22. , 23. , 20.7, 12.5, 48.5,
       14.6, 13.4, 23.7, 50. , 21.7, 39.8, 38.7, 22.2, 34.9, 22.5, 31.1,
       28.7, 46. , 41.7, 21. , 26.6, 15. , 24.4, 13.3, 21.2, 11.7, 21.7,
       19.4, 50. , 22.8, 19.7, 24.7, 36.2, 14.2, 18.9, 18.3, 20.6, 24.6,
       18.2,  8.7, 44. , 10.4, 13.2, 21.2, 37. , 30.7, 22.9, 20. , 19.3,
       31.7, 32. , 23.1, 18.8, 10.9, 50. , 19.6,  5. , 14.4, 19.8, 13.8,
       19.6, 23.9, 24.5, 25. , 19.9, 17.2, 24.6, 13.5, 26.6, 21.4, 11.9,
       22.6, 19.6,  8.5, 23.7, 23.1, 22.4, 20.5, 23.6, 18.4, 35.2, 23.1,
       27.9, 20.6, 23.7, 28. , 13.6, 27.1, 23.6, 20.6, 18.2, 21.7, 17.1,
        8.4, 25.3, 13.8, 22.2, 18.4, 20.7, 31.6, 30.5, 20.3,  8.8, 19.2,
       19.4, 23.1, 23. , 14.8, 48.8, 22.6, 33.4, 21.1, 13.6, 32.2, 13.1,
       23.4, 18.9, 23.9, 11.8, 23.3, 22.8, 19.6, 16.7, 13.4, 22.2, 20.4,
       21.8, 26.4, 14.9, 24.1, 23.8, 12.3, 29.1, 21. , 19.5, 23.3, 23.8,
       17.8, 11.5, 21.7, 19.9, 25. , 33.4, 28.5, 21.4, 24.3, 27.5, 33.1,
       16.2, 23.3, 48.3, 22.9, 22.8, 13.1, 12.7, 22.6, 15. , 15.3, 10.5,
       24. , 18.5, 21.7, 19.5, 33.2, 23.2,  5. , 19.1, 12.7, 22.3, 10.2,
       13.9, 16.3, 17. , 20.1, 29.9, 17.2, 37.3, 45.4, 17.8, 23.2, 29. ,
       22. , 18. , 17.4, 34.6, 20.1, 25. , 15.6, 24.8, 28.2, 21.2, 21.4,
       23.8, 31. , 26.2, 17.4, 37.9, 17.5, 20. ,  8.3, 23.9,  8.4, 13.8,
        7.2, 11.7, 17.1, 21.6, 50. , 16.1, 20.4, 20.6, 21.4, 20.6, 36.5,
        8.5, 24.8, 10.8, 21.9, 17.3, 18.9, 36.2, 14.9, 18.2, 33.3, 21.8,
       19.7, 31.6, 24.8, 19.4, 22.8,  7.5, 44.8, 16.8, 18.7, 50. , 50. ,
       19.5, 20.1, 50. , 17.2, 20.8, 19.3, 41.3, 20.4, 20.5, 13.8, 16.5,
       23.9, 20.6, 31.5, 23.3, 16.8, 14. , 33.8, 36.1, 12.8, 18.3, 18.7,
       19.1, 29. , 30.1, 50. , 50. , 22. , 11.9, 37.6, 50. , 22.7, 20.8,
       23.5, 27.9, 50. , 19.3, 23.9, 22.6, 15.2, 21.7, 19.2, 43.8, 20.3,
       33.2, 19.9, 22.5, 32.7, 22. , 17.1, 19. , 15. , 16.1, 25.1, 23.7,
       28.7, 37.2, 22.6, 16.4, 25. , 29.8, 22.1, 17.4, 18.1, 30.3, 17.5,
       24.7, 12.6, 26.5, 28.7, 13.3, 10.4, 24.4, 23. , 20. , 17.8,  7. ,
       11.8, 24.4, 13.8, 19.4, 25.2, 19.4, 19.4, 29.1])

# 数据标准化

mean = train_data.mean(axis = 0)
print(mean)
train_data = train_data - mean

std = train_data.std(axis = 0)
print(std)
train_data = train_data / std

# 注意，对测试数据也要进行标准化，但是用到的均值和标准差都来源与训练数据

test_data -= mean
test_data /= std

[ 7.83201886e-18 -1.20915379e-17 -1.42899993e-17 -1.21739802e-16
  4.39692287e-18  7.41980734e-18  1.09923072e-17 -1.09923072e-18
 -2.72059603e-17 -2.08853836e-17  1.26411533e-17 -1.23663456e-18
 -3.29769215e-18]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

from keras import models
from keras import layers
def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64,activation = 'relu',input_shape = (train_data.shape[1],)))
    model.add(layers.Dense(64,activation = 'relu'))
    model.add(layers.Dense(1))  #最后一层是一个线性输出单元，不加任何激活函数，他可以与预测任意范围内的值，加了激活函数，就限制了他的输出范围
    model.compile(optimizer = 'rmsprop',loss = 'mse',metrics = ['mae'])
    return model

# 利用k折交叉验证来验证你的方法
import numpy as np

k = 4
num_val_samples = len(train_data) // 4
num_epochs = 100
all_scores = []

for i in range(k):
    print('processing fold ',i)
    val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
    val_target = train_target[i*num_val_samples:(i+1)*num_val_samples]
    
    partial_train_data = np.concatenate([train_data[:i*num_val_samples],train_data[(i+1)*num_val_samples:]],axis = 0)
    partial_train_target = np.concatenate([train_target[:i*num_val_samples],train_target[(i+1)*num_val_samples:]],axis = 0)
    
    model = build_model()
    model.fit(partial_train_data,partial_train_target,epochs = num_epochs,batch_size = 1,verbose = 0)
    val_mse,val_mae = model.evaluate(val_data,val_target,verbose = 0)
    all_scores.append(val_mae)

processing fold  0
processing fold  1
processing fold  2
processing fold  3

print(all_scores)

[2.059201702032939, 2.192299434454134, 2.8599761736274947, 2.4273995509242066]

# 上一个代码块的结果为预测平均房价与实际房价相差300美元左右
# 差别太大，训练更长的时间来看一下效果
num_epochs = 500
all_mae_histories = []
for i in range(k):
    print('processing fold',i)
    val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
    val_target = train_target[i*num_val_samples:(i+1)*num_val_samples]
    
    partial_train_data = np.concatenate([train_data[:i*num_val_samples],train_data[(i+1)*num_val_samples:]],axis = 0)
    partial_train_target = np.concatenate([train_target[:i*num_val_samples],train_target[(i+1)*num_val_samples:]],axis = 0)
    
    model = build_model()
    history = model.fit(partial_train_data,partial_train_target,validation_data = (val_data,val_target),epochs = num_epochs,batch_size = 1,verbose = 0)
    mae_history = history.history['val_mean_absolute_error']
    all_mae_histories.append(mae_history)

processing fold 0
processing fold 1
processing fold 2
processing fold 3

print( len(all_mae_histories))
# print( all_mae_histories)
# 4次交叉验证，每次500次迭代。相当于把4次求平均，还是500个数据
average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]


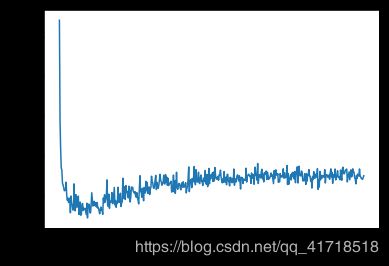
import matplotlib.pyplot as plt
plt.plot(range(1,len(average_mae_history) + 1),average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

# 纵轴范围很大，看不清这张图，删除前10个点，将每个数据点替换为前面数据点的指数移动平均值，以得到光滑曲线
def smooth_curve(points,factor = 0.9):
    smoothed_points = []
    for point in points:
        if smoothed_points:
            previous = smoothed_points[-1]
            smoothed_points.append(previous * factor + point *(1-factor))
        else:
            smoothed_points.append(point)
    return smoothed_points

smooth_mae_history = smooth_curve(average_mae_history[10:])

plt.plot(range(1,len(smooth_mae_history) + 1),smooth_mae_history)

plt.xlabel("Epochs")
plt.ylabel('Validation MAE')
plt.show()

# 重新训练一个模型
model = build_model()
# 在所有的训练数据上训练模型
model.fit(train_data,train_target,epochs = 80,batch_size = 16,verbose = 0)
test_mse_score,test_mae_score = model.evaluate(test_data,test_target)
print(test_mae_score)

102/102 [==============================] - 0s 911us/step
2525.7621256510415

从本例你应该学到以下知识点：

回归模型的损失函数与分类问题的不同，常用均方差损失函数（MSE）
相应的，常用的回归模型指标是平均绝对误差（MAE），确切地说，回归模型没有准确度的概念
输入数据的取值范围不同时，应该在数据预处理阶段将每个特征进行归一化
当数据样本太少时，可以使用K-fold交叉验证稳定的评估一个模型
当训练集数据比较少时，倾向于使用小规模神经网络（一般是一到两个隐藏层），避免过拟合