大话深度信念网络（DBN）

—— 原文发布于本人的微信公众号“大数据与人工智能Lab”（BigdataAILab），欢迎关注。

 

让我们把时间拨回到2006年以前，神经网络自20世纪50年代发展起来后，因其良好的非线性能力、泛化能力而备受关注。然而，传统的神经网络仍存在一些局限，在上个世纪90年代陷入衰落，主要有以下几个原因：
1、传统的神经网络一般都是单隐层，最多两个隐层，因为一旦神经元个数太多、隐层太多，模型的参数数量迅速增长，模型训练的时间非常之久；
2、传统的神经网络，随着层数的增加，采用随机梯度下降的话一般很难找到最优解，容易陷入局部最优解。在反向传播过程中也容易出现梯度弥散或梯度饱和的情况，导致模型结果不理想；
3、随着神经网络层数的增加，深度神经网络的模型参数很多，就要求在训练时需要有很大的标签数据，因为训练数据少的时候很难找到最优解，也就是说深度神经网络不具备解决小样本问题的能力。

由于以上的限制，深度的神经网络一度被认为是无法训练的，从而使神经网络的发展一度停滞不前。

2006年，“神经网络之父”Geoffrey Hinton祭出神器，一举解决了深层神经网络的训练问题，推动了深度学习的快速发展，开创了人工智能的新局面，使近几年来科技界涌现出了很多智能化产品，深深地影响了我们每个人的生活。

那这个神器是什么呢？那就是“深度信念网络”（Deep Belief Network，简称DBN）。

深度信念网络（DBN）通过采用逐层训练的方式，解决了深层次神经网络的优化问题，通过逐层训练为整个网络赋予了较好的初始权值，使得网络只要经过微调就可以达到最优解。而在逐层训练的时候起到最重要作用的是“受限玻尔兹曼机”（Restricted Boltzmann Machines，简称RBM），为什么叫“受限玻尔兹曼机”呢？因为还有一个是不受限的，那就是“玻尔兹曼机”（Boltzmann Machines，简称BM）。
下面依次介绍一下什么是“玻尔兹曼机”（BM）、“受限玻尔兹曼机”（RBM）？

一、玻尔兹曼机（Boltzmann Machines，简称BM）
 
玻尔兹曼机于1986年由大神Hinton提出，是一种根植于统计力学的随机神经网络，这种网络中神经元只有两种状态（未激活、激活），用二进制0、1表示，状态的取值根据概率统计法则决定。
由于这种概率统计法则的表达形式与著名统计力学家L.E.Boltzmann提出的玻尔兹曼分布类似，故将这种网络取名为“玻尔兹曼机”。
在物理学上，玻尔兹曼分布（也称为吉布斯分布，Gibbs Distribution）是描述理想气体在受保守外力的作用（或保守外力的作用不可忽略）时，处于热平衡态下的气体分子按能量的分布规律。
在统计学习中，如果我们将需要学习的模型看成高温物体，将学习的过程看成一个降温达到热平衡的过程（热平衡在物理学领域通常指温度在时间或空间上的稳定），最终模型的能量将会收敛为一个分布，在全局极小能量上下波动，这个过程称为“模拟退火”，其名字来自冶金学的专有名词“退火”，即将材料加热后再以一定的速度退火冷却，可以减少晶格中的缺陷，而模型能量收敛到的分布即为玻尔兹曼分布。
听起来很难理解的样子，只需要记住一个关键点：能量收敛到最小后，热平衡趋于稳定，也就是说，在能量最少的时候，网络最稳定，此时网络最优。

玻尔兹曼机（BM）是由随机神经元全连接组成的反馈神经网络，且对称连接，由可见层、隐层组成，BM可以看做是一个无向图，如下图所示：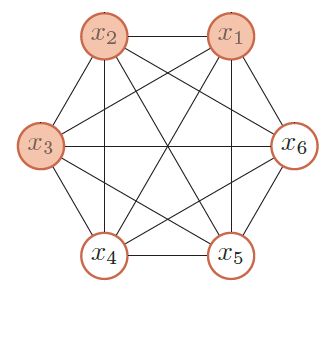
 
其中，x1、x2、x3为可见层，x4、x5、x6为隐层。
整个能量函数定义为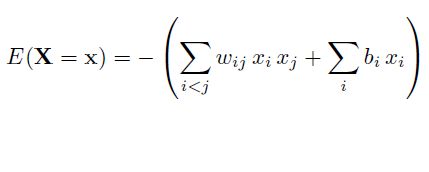
 
其中，w为权重，b为偏置变量，x只有{0,1}两种状态。
根据玻尔兹曼分布，给出的一个系统在特定状态能量和系统温度下的概率分布，如下：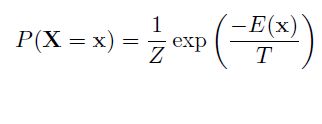
 
前面讲过，“能量收敛到最小后，热平衡趋于稳定”，因此：
1、简单粗暴法
要寻找一个变量使得整个网络的能量最小，一个简单（但是低效）的做法是选择一个变量，在其它变量保持不变的情况下，将这个变量设为会导致整个网络能量更低的状态。那么一个变量Xi的两个状态0（关闭）和1（打开）之间的能量差异为：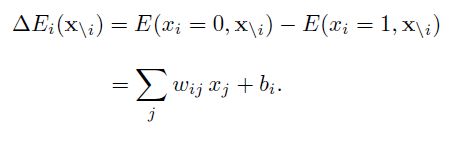
 
这时，如果能量差异ΔE大于一定的阈值（比如0），我们就设Xi = 1（也即取能量小的），否则就设Xi = 0。这种简单的方法通过反复不断运行，在一定时间之后收敛到一个解（可能是局部最优解）。
2、最大似然法
利用“模拟退火”原理寻找全局最优解，根据玻尔兹曼分布，Xi=1的概率为：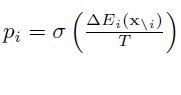
 
训练集v的对数似然函数为：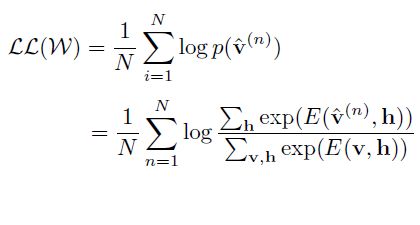
 
对每个训练向量p(v)的对数似然对参数w求导数，得到梯度：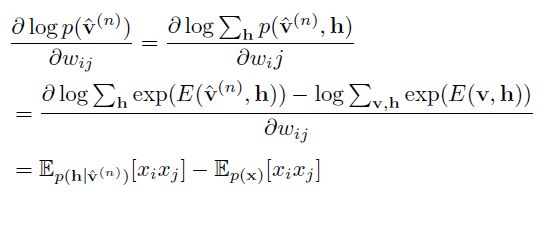
 
跟传统的神经网络类似，参数w的更新公式如下（a为学习率）：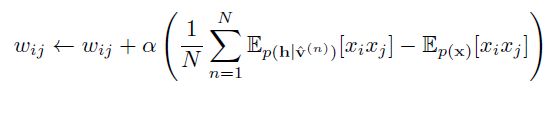
     
好了好了，公式就讲到这里了，看上去挺复杂的，没错，确实计算很复杂，这个梯度很难精确计算，整个计算过程会十分地耗时。
目前，可以通过一些采样方法（例如Gibbs采样）来进行近似求解。

玻尔兹曼机（BM）可以用在监督学习和无监督学习中。在监督学习中，可见变量又可以分为输入和输出变量，隐变量则隐式地描述了可见变量之间复杂的约束关系。在无监督学习中，隐变量可以看做是可见变量的内部特征表示，能够学习数据中复杂的规则。玻尔兹曼机代价是训练时间很长很长很长。

二、受限玻尔兹曼机（Restricted Boltzmann Machines，简称RBM）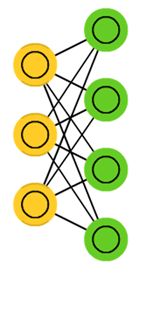
 
所谓“受限玻尔兹曼机”（RBM）就是对“玻尔兹曼机”（BM）进行简化，使玻尔兹曼机更容易更加简单使用，原本玻尔兹曼机的可见元和隐元之间是全连接的，而且隐元和隐元之间也是全连接的，这样就增加了计算量和计算难度。
“受限玻尔兹曼机”（RBM）同样具有一个可见层，一个隐层，但层内无连接，层与层之间全连接，节点变量仍然取值为0或1，是一个二分图。也就是将“玻尔兹曼机”（BM）的层内连接去掉，对连接进行限制，就变成了“受限玻尔兹曼机”（RBM），这样就使得计算量大大减小，使用起来也就方便了很多。如上图。
“受限玻尔兹曼机”（RBM）的特点是：在给定可见层单元状态（输入数据）时，各隐层单元的激活条件是独立的（层内无连接），同样，在给定隐层单元状态时，可见层单元的激活条件也是独立的。

跟“玻尔兹曼机”（BM）类似，根据玻尔兹曼分布，可见层（变量为v，偏置量为a）、隐层（变量为h，偏置量为b）的概率为：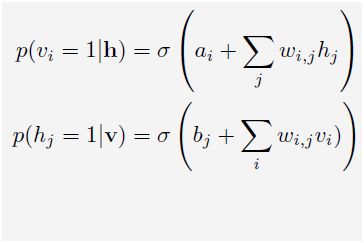
 
训练样本的对数似然函数为：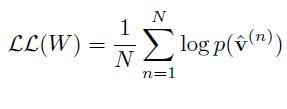
 
求导数：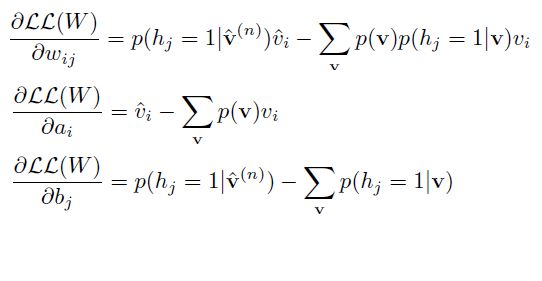
 
总之，还是挺复杂的，计算也还是挺花时间的。
同样，可以通过Gibbs 采样的方法来近似计算。虽然比一般的玻尔兹曼机速度有很大提高，但一般还是需要通过很多步采样才可以采集到符合真实分布的样本。这就使得受限玻尔兹曼机的训练效率仍然不高。
2002年，大神Hinton再出手，提出了“对比散度”（Contrastive Divergence，简称CD）算法，这是一种比Gibbs采样更加有效的学习算法，促使大家对RBM的关注和研究。

RBM的本质是非监督学习的利器，可以用于降维（隐层设置少一点）、学习提取特征（隐层输出就是特征）、自编码器（AutoEncoder）以及深度信念网络（多个RBM堆叠而成）等等。

三、深度信念网络（Deep Belief Network，简称DBN）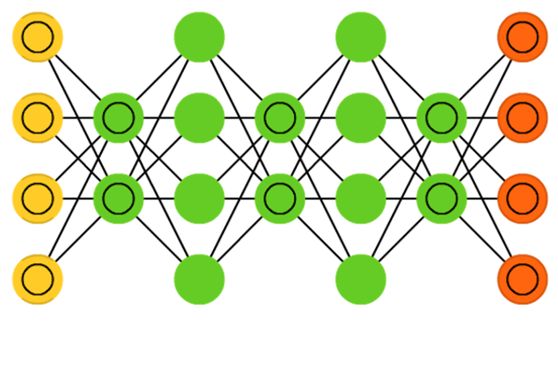
 
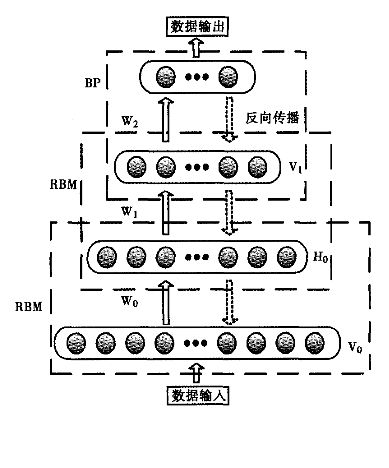
2006年，Hinton大神又又又出手了，提出了“深度信念网络”（DBN），并给出了该模型一个高效的学习算法，这也成了深度学习算法的主要框架，在该算法中，一个DBN模型由若干个RBM堆叠而成，训练过程由低到高逐层进行训练，如下图所示：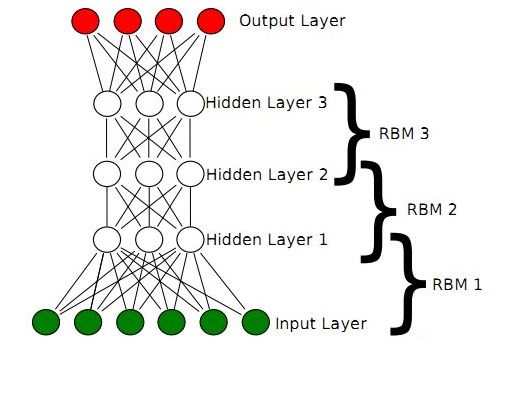
 
回想一下RBM，由可见层、隐层组成，显元用于接受输入，隐元用于提取特征，因此隐元也有个别名，叫特征检测器。也就是说，通过RBM训练之后，可以得到输入数据的特征。（感性对比：联想一下主成分分析，提取特征）
另外，RBM还通过学习将数据表示成概率模型，一旦模型通过无监督学习被训练或收敛到一个稳定的状态，它还可以被用于生成新数据。（感性对比：联想一下曲线拟合，得出函数，可用于生成数据）

正是由于RBM的以上特点，使得DBN逐层进行训练变得有效，通过隐层提取特征使后面层次的训练数据更加有代表性，通过可生成新数据能解决样本量不足的问题。逐层的训练过程如下：
（1）最底部RBM以原始输入数据进行训练
（2）将底部RBM抽取的特征作为顶部RBM的输入继续训练
（3）重复这个过程训练以尽可能多的RBM层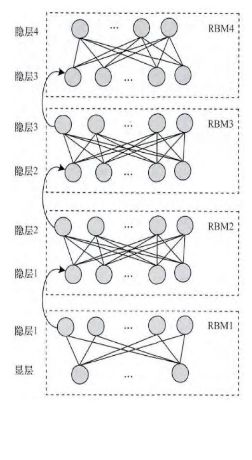
 
由于RBM可通过CD快速训练，于是这个框架绕过直接从整体上对DBN高度复杂的训练，而是将DBN的训练简化为对多个RBM的训练，从而简化问题。而且通过这种方式训练后，可以再通过传统的全局学习算法（如BP算法）对网络进行微调，从而使模型收敛到局部最优点，通过这种方式可高效训练出一个深层网络出来，如下图所示：

Hinton提出，这种预训练过程是一种无监督的逐层预训练的通用技术，也就是说，不是只有RBM可以堆叠成一个深度网络，其它类型的网络也可以使用相同的方法来生成网络。

 

墙裂建议

Hinton 大神写了一篇关于受限玻尔兹曼机的训练实用指南（《A Practical Guide to Training Restricted Boltzmann Machines》），非常详细地描述训练过程，建议仔细阅读下这篇论文，肯定大有收获。

扫描以下二维码关注本人公众号“大数据与人工智能Lab”（BigdataAILab），然后回复“论文”关键字可在线阅读这两篇经典论文的内容。

 

推荐相关阅读

• 大话卷积神经网络（CNN）
• 大话循环神经网络（RNN）
• 大话深度残差网络（DRN）
• 深度学习中常用的激励函数