数据降维 | 奇异值分解(SVD) 、推荐系统、图像压缩
01 PCA.改
在上一篇文章中,我们学习并实践了一种主流的数据降维算法——主成分分析(PCA)。
我们再来回顾一下PCA的优缺点:
- 优点:降低数据复杂性,识别最重要的多个特征
- 缺点:PCA需要将所有数据集放入内存,若数据集较大,内存处理效率低,此时需要使用其他方法来寻找特征值
基于PCA算法在处理大数据集时内存处理效率较低的缺点,出现了一种更加高效的降维算法——奇异值分解(SVD),本文简单介绍SVD算法的原理,并通过python实现,然后运用在推荐系统中(基于用户的推荐)
好了,系好安全带,开车了!
02 SVD原理
奇异值分解其实是线性代数中的概念,是矩阵分解的一种方法,其中,
- 矩阵分解:将原始矩阵表示成两个或多个矩阵乘积的形式,使得易于处理(类比代数因子分解)。
- 奇异值分解(SVD)是矩阵分解方法的一种:

类似PCA,PCA算法中,数据的信息藏在前n个特征值中,SVD算法中,数据的信息藏在前n个奇异值中。
对于刚才奇异值分解的原理论述中,矩阵分解是这样进行的,

因此,当我们在进行SVD时,我们其实是在找这三个简化的矩阵,这三个简化的矩阵相乘后,可以得到与原始矩阵近似的矩阵。
从而,利用SVD的这个特性,我们可以做些什么呢?想想,比如,
- 图像压缩:用简化后的矩阵代表原始图像
- 数据降维:找到多维数据背后的关系,整合成少数特征 (推荐系统常用预处理方法)
- 等等等等
了解了SVD原理,下面我们用python实操一波,然后应用在一个简单的推荐系统中。
03 Python实现之应用于推荐系统
在实现SVD前,先来了解一下推荐系统的协同过滤法,
- 通过将用户和其他用户的评分数据进行比较实现推荐
- 不关心物品的描述属性(如汉堡描述属性:高热量,碳水化合物等等),不使用物品的客观描述属性而使用用户对物品的意见来计算相似度
什么意思呢,协同过滤就是用户对物品的打分结果,对用户进行物品推荐,举个例子,当我们听虾米音乐时,对于你喜欢的歌,你会点赞或下载,这相当于你对歌曲进行了打分,然后虾米会根据你的历史打分记录与别的用户的打分记录,对你未听过的歌曲进行推荐。
p.s. 另一种方推荐算法是基于内容的推荐,即根据歌曲的类型如摇滚、古典等,结合你的听歌喜好进行推荐
好了,回到正题,SVD。我们知道,在推荐系统中,用户数常常远大于物品数,每个用户只会对少量的物品进行打分,如果把用户和物品得分构成一个矩阵,这会是一个较大的稀疏矩阵,因此在进行推荐之前,需要用到SVD进行矩阵的简化(即,降维),从而大大提升推荐系统的效率和效果。
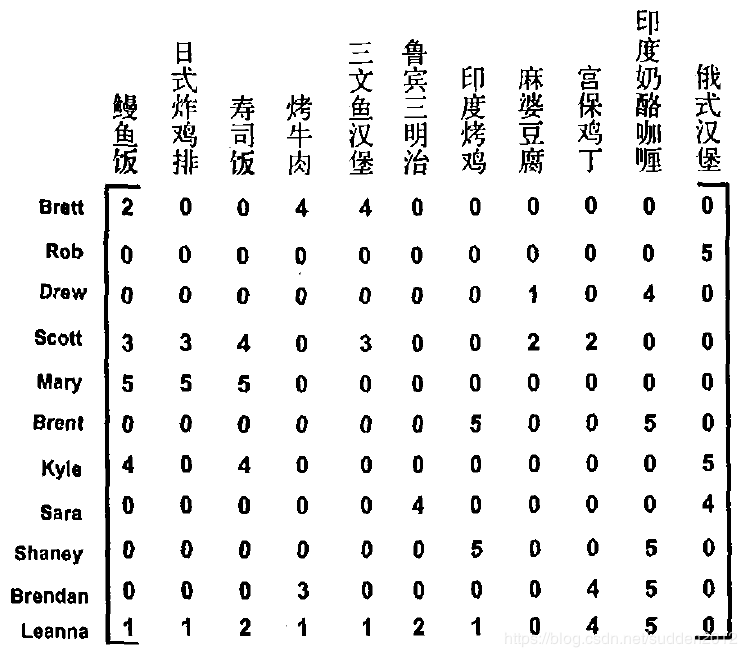
假设我们有这么一个用户打分数据(数据示例,非代码实际使用数据),该如何对用户进行菜品推荐呢?
过程
- SVD去除数据噪声
- 遍历该用户已评分物品j,利用其他对物品j和item都评分的用户的评分,计算物品j和item的相似度
- 将相似度*该用户评分求和再除以simTotal归一化,得到针对该用户的物品item的推荐程度数值(值越大说明越推荐)
实操一波,
#三种相似度度量
def ecludSim(inA,inB):
return 1.0/(1.0+linalg.norm(inA-inB)) #linalg.norm(inA-inB)为欧式距离,通过公式变换,将欧式距离相似度范围限制在[0,1],且相似度越高,值越大
def pearsSim(inA,inB):
if len(inA)<3:
return 1.0 #若不存在3个及以上的点,则返回1,表示两个向量完全相关(根据相关系数公式,当向量少于3个点时,计算为1)
return 0.5+0.5*corrcoef(inA,inB,rowvar=0)[0][1] #rowvar=0将AB列作为样本,公式变换将相似度范围限制在[0,1]
def cosSim(inA,inB):
num=float(inA.T*inB)
denom=linalg.norm(inA)*linalg.norm(inB)
return 0.5+0.5*(num/denom)
def svdEst(dataMat,user,simMeas,item):
n=shape(dataMat)[1]
simTotal=0.0
rateSimTital=0.0
"""SVD加入:奇异值分解、选择、降维"""
U,Sigma,VT=linalg.svd(dataMat)
k=nonzero(cumsum(Sigma**2)/cumsum(Sigma**2)[-1]>0.9)[0][0]+1 #寻找信息量占比超过90%需要的奇异值个数
Sigk=mat(eye(k)*Sigma[:k]) #构造k维奇异值矩阵
xformedData=dataMat.T*U[:,:k]*Sigk.I #将原始数据转换到低维空间,原理见上,xformedData形状为n*k
for j in range(n): #遍历各物品,使用j而不是i,是为了突出遍历的是dataMat的列
userRating=dataMat[user,j]
if userRating==0.0 or j==item: #跳过该用户未评分的(即未体验过的)物品
continue
similarity=simMeas(xformedData[item,:],xformedData[j,:])
#print ("The %d and %d similarity is: %.2f"%(item,j,similarity))
#simTotal代表物品item与其他物品的相似度之和,rateSim乘上了该用户对物品j的评分
simTotal+=similarity
rateSimTital+=similarity*userRating
if simTotal==0:
return 0.0
else:
return round(rateSimTital/simTotal,2) #归一化相似度,使范围在[1,5]
#N为待推荐的物品数目
def recommend(dataMat,user,N=3,simMeas=cosSim,estMethod=standEst):
unratedItems=nonzero(dataMat[user,:].A==0)[1]
if len(unratedItems)==0:
return ("You rated everything.")
itemScores=[]
for item in unratedItems:
estimatedScore=estMethod(dataMat,user,simMeas,item)
itemScores.append((item,estimatedScore))
return sorted(itemScores,key=lambda scores:scores[1],reverse=True)[:N]
来看看运行效果,下面是原始打分数据,

下面是推荐结果,推荐系统给第三个用户推荐了第3个,第2个物品

04 Python实现之应用于图像压缩
接下来,我们看看SVD应用在图像压缩的效果,原图像如下,

SVD图像压缩代码如下,
def printMat(inMat,thresh=0.8):
for i in range(32):
for k in range(32):
if float(inMat[i,k])>thresh:
print (1,end="")
else:
print (0,end="") #默认end="\n"表示print后换行,end=" 表示print后不换行
print ('') #用于换行
def imgCompress(numSV=3,thresh=0.8):
myl=[]
for line in open(r'D:\0_5.txt').readlines():
newRow=[]
for i in range(32):
newRow.append(int(line[i]))
myl.append(newRow)
myMat=mat(myl)
print ("*******原始图像******")
printMat(myMat,thresh)
U,Sigma,VT=linalg.svd(myMat)
Sig=mat(eye(numSV)*Sigma[:numSV])
reconMat=U[:,:numSV]*Sig*VT[:numSV,:]
print ("*******压缩图像******")
printMat(reconMat,thresh)
保留二维奇异矩阵压缩后,图像如下,同学们可以比较一下两幅图01的差异,压缩后图像的1少了很多,但我们还是能够识别出来这个图像是个“零”,这就是基于SVD的图像压缩。

05 总结
本文简单介绍了SVD原理,然后用python实现,并应用在推荐系统和图像压缩中,目前很多大型推荐系统都采用了SVD预处理数据的方式,但SVD还是有些缺点:
- 对于较大数据集,每次推荐都做SVD是很耗资源的,因此SVD一般在调入数据时运行一次,有的大型系统每天运行一次SVD或更低频
- 冷启动问题:如何在缺乏数据时给出好的推荐?–>解法:将推荐问题看作搜索问题。需要物品的客观描述属性来标记物品,从而计算相似度,这种又叫做“基于内容的推荐”
对于推荐系统的冷启动问题,还会采用引导新用户自己填写问卷的方式收集新用户偏好数据,比如你新注册一个Amazon账号,它会引导你勾选几本你喜欢的书……
SVD的介绍和实操到此结束,希望对你有帮助~
06 参考
《机器学习实战》 Peter Harrington Chapter14