图深度学习 Deep Learning on Graph

Zhang Z , Cui P , Zhu W . Deep Learning on Graphs: A Survey[J]. 2018.

深度学习在大量领域表现出明显的效果，无论是语音，图像，还是自然语言处理。但是由于图结构数据具有独特的属性，深度学习并不是自然的适用。最近，在这个方向进行了大量的研究极大地促进了图分析技术。调研了可以应用于图的不同种类深度学习方法，主要分为三大类：半监督学习，包括图神经网络和图卷积神经网络；无监督学习图自编码机；最新的进展，图循环神经网络和图强化学习。分析了不同方法的特点和联系。

引言

表示目标和目标间的关系的图在现实生活中处处存在，比如社交网络，电子商务网络，生物网络和交通网络等。同时由于蕴含着吩咐的潜在信息，图也被公认为是能以深刻理解的结构。
过去十年中，深度学习称为人工智能和机器学习中极为重要的部分，在音频、图像和自然语言处理等方面表现出优越的性能，在提取数据中潜在复杂模式有着明显的效果。
因此如何利用深度学习的方法对图数据进行分析在过去几年中吸引了广泛的关注。这个问题并不是对深度学习简单的推管，下面给出在图上应用传统深度学习框架的部分难点和挑战：

• 非规则域。与图像，音频和文本这类清晰的网格化结构不同，图的结构是不规则的，这也使得难以将简单的数值计算应用到图上。比如，不能对图数据直接定义卷积和池化操作。这里需要考虑的就是被称为的几何学深度学习问题。
• 多样的结构和任务。图本身就具有复杂的多样化结构，比如图可以是同质的或异质的，赋权或非赋权，标定或非标定的。另外图上的任务也是多样化的，有针对图顶点的问题，例如节点分类，链路预测；也有针对图的问题，比如图分类和图生成。
• 可拓展性与并行性。在大数据时代，现实中的图规模很大，很轻松就能够达到数以百万计的节点和边，如社交网络，电商网络。因此如何设计可拓展的模型期望能够达到线性时间复杂度，称为一个关键的问题。图中的节点和边是互相关联的，一些场景就需要将整体统一考虑，解决并行计算问题也至关重要。
• 学科交叉。图和其他学科关联紧密，例如生物学、化学和社会科学等。领域知识能够解决特定的问题，知识的整合却能导致模型设计的复杂性。比如生成分子图，此时的目标函数和化学约束往往是不可微的，通常基于梯度的训练方法就变得不再适用。

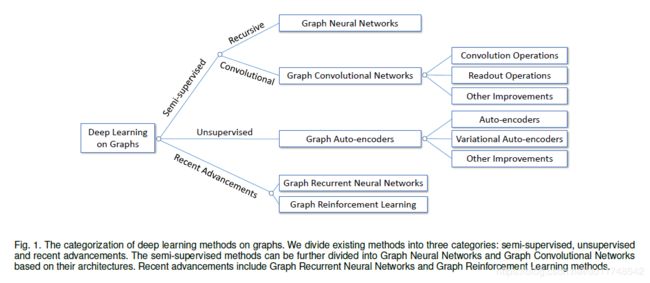
如Fig 1，将现有的方法主要分为三大类：

• 半监督方法。图神经网络，图卷积神经网络。
• 无监督方法。图自编码机。
• 最新的进展。图循环神经网络，图强化学习。

这些方法的主要区别如Table 1所示。GNNs和GCNs利用节点特征和节点标签对网络进行训练，GAEs使用无监督学习方法进行表示学习。

图神经网络

图神经网络(Graph Neural Networks, GNNs)是最早明确针对图数据的半监督深度学习方法。详情见：图神经网络模型。GNNs为了达到图的稳定状态，假设扩散函数是一个压缩映射，限制了建模能力，同时为了达到图的稳定状态，需要在梯度下降步之间进行多次迭代，计算复杂度高。
GNNs经过不断改进，应用广泛：CommNet, Interaction Network, VAIN, Relation Networks.

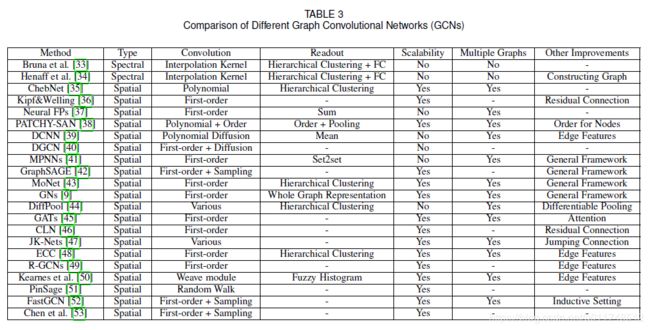
图卷积网络

图卷积网络(Graph Convolutional Networks, GCNs)总结如Table 3所示，其中一类图卷积网络可详见：图卷积网络。

卷积操作

谱方法

卷积是卷积神经网络CNNs中最基本的操作，但是由于图不具备网格结构，针对图像和文本的标准卷积并能够直接应用于图。Bruna等首先从谱域中使用图的拉普拉斯矩阵$L$，引入了图数据上的卷积。此时图G上卷积操作定义为：
$$u{\ast }_{G}g=Q^T(Qu\odot Qg),（1）$$其中，$u,g\in {\mathbb{R}}^N$分别是输入信号和过滤器，$Q$是$L$的特征矩阵。进一步，可以得到
$$u^{\prime }=u{\ast }_{G}g=Q^T\Theta Qu,（2）$$$u^{\prime }$是输出信号，$\Theta =\Theta (\Lambda )\in {\mathbb{R}}^{N\times N}$是可学习的对角阵。然后每一个卷积层 $l$ 可以被定义为：
$$u_j^{l+1}=\rho (\sum _{i=1}^{f_l}{Q}^T\Theta Q{u}_i^l),j=1,\cdots ,f_{l+1}(3)$$

直接使用上式需要对$o$$(N)$个参数进行学习，在实际应用中不够灵活。Bruna等人建议使用下面光滑的过滤器，$\mathcal{K}$表示固定的插值核，${\alpha }_{l,i,j}$是需学习的插值系数：
$$diag({\Theta }_{i,j}^l)=\mathcal{K}{\alpha }_{l,i,j}(4)$$

Efficiency Aspect

ChebNet使用多项式过滤器，${\theta }_0,\cdots ,{\theta }_{K-1}$是需学习的参数：$$\Theta (\Lambda )=\sum _{k=0}^{K-1}{\theta }_k{\Lambda }^k(5)$$
对特征分解进行估计，采用chebyshev多项式进行拟合，$\tilde{\Lambda }=2\Lambda /{\lambda }_{max}-I$是缩放过的特征矩阵。$$\Theta (\Lambda )=\sum _{k=0}^{K-1}{\theta }_k{\mathcal{T}}_k(\tilde{\Lambda })(6)$$
${\bar{u}}_k={\mathcal{T}}_k(\tilde{L})u,\tilde{L}=2L/{\lambda }_{max}-I$：
$$u^{\prime }=Q^T\Theta (\Lambda )Qu=\sum _{k=0}^{K-1}{\theta }_k{Q}^T{\mathcal{T}}_k(\tilde{\Lambda })Qu=\sum _{k=0}^{K-1}{\theta }_k{\mathcal{T}}_k(\tilde{L})u=\sum _{k=0}^{K-1}{\theta }_k{\bar{u}}_k(7)$$

Kipf, Welling通过取一跳邻点和chebyshev多项式的一阶近似简化上述公式：
$$H^{l+1}=\rho ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^l{\Theta }^l)(8)$$

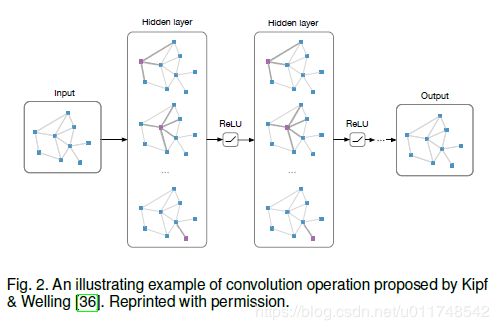
此一类图卷积网络可详见：图卷积网络。其架构如Figure 2所示。

Multiple Graphs Aspect

Neural FPs 对一跳邻点使用spatial method：
$$h_i^{l+1}=\sigma (\sum _{j\in \hat{\mathcal{N}}(i)}{h}_j^l{\Theta }^l)(9)$$
$\Theta$不同图共享独立于图的规模，即Neural FPs 可以处理多个不同规模的图，适用于小规模的图。

PATCHY-SAN 对每个顶点定义了一个可接纳域，从k跳邻域中选择固定数目的顶点，然后使用标准的1-D CNN处理。

DCNN 使用扩散机制替代卷积中的特征基，即可接受域中的节点通过节点间的扩散转移概率确定。$P^K$是长度为$K$的扩散机制的转移慨率，比如随机游走，此时卷积定义为：
$$H^{l+1}=\rho (P^K{H}^l{\Theta }^l)(10)$$

DGCN 将扩散和邻接机制融合，使用对偶图卷积网络，有两种卷积，一类如公式(8)，另一类使用转移概率的 positive 逐点互信息(PPMI)矩阵$X_P$替换邻接矩阵,$D_P(i,i)={\sum }_{j̸=i}{X}_P(i,j)$：
$$Z^{l+1}=\rho (D_P^{-\frac{1}{2}}{X}_P{D}_P^{-\frac{1}{2}}{Z}^l{\Theta }^l)(11)$$
两种卷积通过最小化$H,Z$的均方差进行聚合。

框架

基于上面两项工作，MPNNs 通过谱域种图卷积操作构建了统一的框架,${\mathcal{F}}^l,{\mathcal{G}}^l$分别是消息传播函数和顶点更新函数：
$$m_i^{l+1}=\sum _{j\in \mathcal{N}(i)}{\mathcal{F}}^l(h_i^l,h_j^l,F_{i,j}^E)$$$$h_i^{l+1}={\mathcal{G}}^l(h_i^l,m_i^{l+1})(12)$$
从概念上讲，MPNN 提出的框架，每个节点根据其状态发送消息，并根据从直接邻域顶点收到的消息更新其状态。同时添加一个“主”节点，该节点连接到所有节点以加速长距离时的消息传递。
GraphSAGE 采用了多聚合函数与上述方法类似：
$$m_i^{l+1}=AGGREGAT{E}^l(\{h_i^l,\forall j\in \mathcal{N}(i\})$$$$h_i^{l+1}=\rho ({\Theta }^l[h_i^l,m_i^{l+1}])(13)$$给出了三个建议的聚合函数：

• element-wise mean
• LSTM
• pooling$AGGREGAT{E}^l=\max \{\rho ({\Theta }_{pool}{h}_j^l+b_{pool}),\forall j\in \mathcal{N}(i)\}(14)$

Mixture Model Network (MoNet) 尝试使用 $template$ $matching$ 将GCN和CNN先前的工作整合到一个统一框架。
$$h_{ik}^{l+1}=\sum _{j\in \mathcal{N}(i)}{\mathcal{F}}_k^l(u(i,j))h_j^l,k=1,\cdots ,f_{l+1}(15)$$$${\mathcal{F}}_k^l(u)=\exp (-\frac{1}{2}(u-{\mu }_k^l{)}^T({\Sigma }_k^l{)}^{-1}(u-{\mu }_k^l))(16)$$$$u(i,j)=(D(i,i{)}^{-\frac{1}{2}},D(j,j{)}^{-\frac{1}{2}})(17)$$

Graph Network (GNs) 给出了一个对GCNs和GNNs都通用更为一般的框架，学习图上三个集合的表示：顶点，边和图$h_i^l,e_{ij}^l,z^l$：
$$m_i^l={\mathcal{G}}^{E\to V}(\{h_j^l,\forall j\in \mathcal{N}(i)\})$$$$m_V^l={\mathcal{G}}^{V\to G}(\{h_j^l,\forall v_i\in V\})$$$$m_E^l={\mathcal{G}}^{E\to G}(\{h_{ij}^l,\forall (v_i,v_j)\in E\})$$$$h_i^{l+1}={\mathcal{F}}^V(m_i^l,h_i^l,z^l)$$$$e_{ij}^{l+1}={\mathcal{F}}^E(e_{ij}^l,h_i^l,h_i^l,z^l)$$$$z^{l+1}={\mathcal{F}}^G(m_E^l,m_V^l,z^l)(18)$$

卷积运算从谱域演变为空间域，并且从多步邻域顶点演变为直接邻域顶点。目前，(12),(13),(18)是图卷积运算的最常见选择。

Readout 操作

通过卷积操作，可以学习到节点有价值的特征，此时主要解决针对节点的任务。为了进一步处理面向图的任务，获取的顶点信息需要聚合为图层次的表示。在文献中，称为Readout或图粗化操作，这个问题并不是可以直接套用的，因为CNNs中带步长的卷积或者池化操作在非网格结构下不能直接使用。

序列不变性。图Readout操作的一个关键条件时节点的序列不变性，即构建一个双射将原图中的节点和边投影为新生成的图的点和边，但是在投影后的图上学得的图表示与前者相同。
后续补充

• 统计学
• 分层聚类
• 其他

改进与讨论

注意力机制

在以前的GCN中，给邻域顶点赋予相等的或者预定义的权重，但是这些邻域顶点具有很大差别的影响力，在训练中学习优于预先设定。
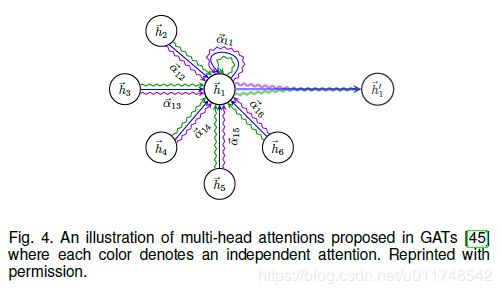
图注意力网络(Graph Attention Network, GATs) 及那个注意力机制引入GCNs：
$$h_i^{l+1}=\rho (\sum _{j\in \hat{N}(i)}{\alpha }_{ij}^l{h}_j^l{\Theta }^l)$$$${\alpha }_{ij}^l=\frac{\exp (LeakyReLU(\mathcal{F}(h_i^l{\Theta }^l,h_j^l{\Theta }^l)))}{{\sum }_{k\in \hat{\mathcal{N}}(i)}\exp (LeakyReLU(\mathcal{F}(h_i^l{\Theta }^l,h_k^l{\Theta }^l)))}$$

残差和跳跃连接 Residual and Jumping Connections

残差连接被添加进GCNs中，用一条过某些特定的层，这种操作可以增大网络的深度，比如 Kipf添加如下：
$$H^{l+1}=\rho ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^l{\Theta }^l)+H^l$$

Jumping Knowledge Networks(JK-Nets) 连接网络的最后一层和所有的隐层，即跳过所有的表示到最后的输出，可以有选择的利用不同区域的信息, $h_i^{final}$ 示节点$v_i$的最终表示：
$$h_i^{final}=AGGREGATE(h_i^0,h_i^1,\cdots ,h_i^K)$$

边特征 Edge Features

以前的GCNs更多的关注于节点特征的利用，但是边特征中也蕴含着丰富且重要的资源。
对于简单的离散值边特征，如边的类型，可以直接对不同的边类型训练不同的参数，最后整合结果。Neural FPs 对不同度的节点训练不同的参数，对应于分子图中不同键类型所蕴含的边特征，并对结果求和。 CLN 对异质图中不同的边类型训练不同的参数，对结果取平均。Edge-Conditioned Convolution (ECC) 基于边的类型训练不同的参数，应用于图分类。Relational GCNs (R-GCNs) 借鉴知识图谱中的方法对不同关系类型训练不同权重。上述方法只能够处理受限的离散边特征。

DCNN 将每条边转化为一个节点，并加入新边连接原来的两个端点，将边特征转换为点特征处理。
Kearnes等设计了一种 weave 模块，学习节点和边的表示，并且在这之间交换信息。weave模块包含四个不同的函数 Node-to-Node(NN), Node-to-Edge(NE), Edge-to-Edge(EE), Edge-to-Node(EN)：
$$h_i^{l^{\prime }}={\mathcal{F}}_{NN}(h_i^0,h_i^1,\cdots ,h_i^l)$$

$$h_i^{l^{\prime \prime }}={\mathcal{F}}_{EN}(\{e_{ij}^l|j\in \mathcal{N}(i)\})$$

$$h_i^{l+1}={\mathcal{F}}_{NN}(h_i^{\prime },h_i^{\prime \prime })$$

$$e_{ij}^{l^{\prime }}={\mathcal{F}}_{EE}(e_{ij}^0,e_{ij}^1,\cdots ,e_{ij}^l)$$

$$e_{ij}^{l^{\prime \prime }}={\mathcal{F}}_{NE}(h_i^l,h_j^l)$$

$$e_{ij}^{l+1}={\mathcal{F}}_{EE}(e_{ij}^{l^{\prime }},e_{ij}^{l^{\prime \prime }})$$

Accelerating by Sampling

GCNs 在大规模图上训练的有效性问题，是一个关键的瓶颈，考虑算法执行的加速方法。
前文所述，很多GCNs 都使用聚合邻域信息的框架，但是在真实网络服从幂律分布，即少部分点有大度数，邻域扩展增长很快。为了解决这个问题，GraphSAGE 对每个顶点取相同数量的邻域顶点；PinSage 应该图上的随机游走方法抽取邻域顶点。FastGCN 对卷积层中的节点进行抽样，此时将节点视为独立同分布的样本，图卷积作为概率度量下的积分变换。

图自编码机 Graph Autoencoders (GAEs)

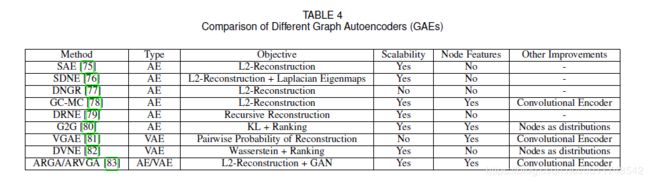
自编码机广泛应用于非监督学习，适用于没有监督信息图的节点表示学习。不同图自编码机的比较如 Table 4 所示。

自编码机

应用于图的自编码机起源于稀疏自编码机(Spare Autoencoder, SAE)。基本的想法是将邻接矩阵作为顶点的原始特征，利用自编码机降维技术来学习节点的低维表示。特别的，SAE采用下面的L2-重建损失，$P$是过度矩阵，$\hat{P}$是重建矩阵，$h_i\in {\mathbb{R}}^d$是顶点$v_i$的低维表示，$\mathcal{F}(\cdot ),\mathcal{G}(\cdot )$分别是编码器和解码器，可学习参数$\Theta$：
$$\underset{\Theta }{\min }{\mathcal{L}}_2=\sum _{i=1}^N\Vert P(i,:)-\hat{P}(i,:){\Vert }_2$$

$$\hat{P}(i,:)=\mathcal{G}(h_i),h_i=\mathcal{F}(P(i,:))(12)$$

编码器和解码器都是多层感知机，SAE 尝试将$P(i,:)$的信息压缩到低维的向量$h_i$然后重建为原始向量。学习得到低维表示后，使用k-mean方法对节点进行聚类。

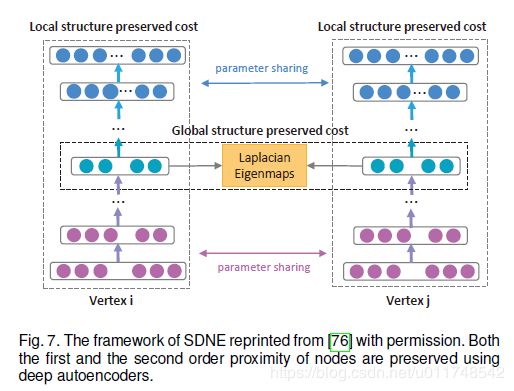
结构化深度网络潜入(Struture Deep Network Embedding, SDNE)揭示了上式中的L重建损失对应于二阶近似，即两个具有相似邻域节点的表示相似，这在网络科学中得到了很好的研究，例如协同过滤或三角形闭包。基于一阶近似方法，SDNE修正了上述式子，添加了一个近似拉普拉斯映射项。
$$\underset{\Theta }{\min }{\mathcal{L}}_2+\alpha \sum _{i,j=1}^{N}A(i,j)\Vert h_i-h_j{\Vert }_2$$
此时如果两个节点直接相邻则需要共享相似的表示。这里$L_2$重建损失函数也做了修改，使用了邻接矩阵和制定的权重，如果$A(i,j)=0,b_{ij}=1$；否则$b_{ij}=\beta >1$，$\beta$是超参数。SDNE整体架构如Figure 7示。
$${\mathcal{L}}_2=\sum _{i=1}^N\Vert (A(i,:)-\mathcal{G}(h_i))\odot b_i{\Vert }_2$$

DNGR 使用随即冲浪概率(Random Surfing Probability)的PPMI矩阵替换过度矩阵式中的$P$。行特征于随机游走概率相关联。

GC-MC 进一步使用GCN作为编码器，简单的双线性函数作为解码器，对于没有节点特征的图，可以对节点惊醒one-hot编码。
$$H=GCN(F^V,A),\hat{A}(i,j)=H(i,:){\Theta }_{de}H(j,:{)}^T$$

DRNE 通过LSTM聚合邻域信息，直接重建节点的低维向量。邻接节点通过度数进行排列。
$$\mathcal{L}=\sum _{i=1}^N\Vert h_i-LSTM(\{h_j|j\in \mathcal{N}(i)\})\Vert$$

和上述映射节点为低维向量的工作不同，Graph3Gauss (G2G) 用高斯分布对每个节点编码$h_i=\mathcal{N}(M(i,:),diag(\Sigma (i,:)))$，进而达到顶点的不确定性。使用节点属性高斯分布的平均值和方差深度映射作为编码器：
$$M(i,:)={\mathcal{F}}_M(F^V(i,:),\Sigma (i,:))={\mathcal{F}}_{\Sigma }(F^V(i,:))$$

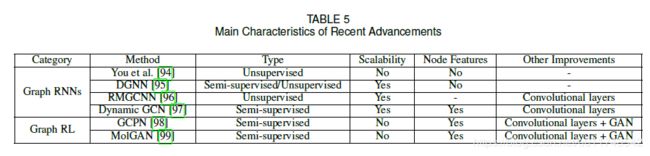
最新成果

图循环神经网络(Graph Recurrent Neural Networks)

循环神经网络如GRU，LSTM对时序数据建模，被GNNs应用于对节点状态建模。本节，将描述在图层次应用RNN，称之为Graph RNNs。You 等应用于图生成问题，他们应用了两个RNNs，一个负责生成新节点，同时另一个采用自回归的方式负责对新添加的节点生成边。

动态图神经网络(Dynamic Graph Neural Network, DGNN)使用LSTM学习动态图的节点表示。在一条边建立后，DGNN使用LSTM对两个相关的节点及直接邻域进行更新。

图强化学习(Graph Reinforcement Learning)

强化学习能够处理不可微的目标和约束。
GCPN 利用强化学习进行目标导向的分子图生成任务，以处理不可微目标和约束。使用马尔科夫决策过程建模图的生成，将生成模型视为在图生成环境中操作的强化学习代理。

总结与讨论

给出基于图的深度学习方法的应用于未来的方向。
Applications

• 标准的图推理任务：节点和图分类
• 社交影响力建模
• 推荐系统
• 化学
• 物理
• 疾病药物预测
• 自然语言处理
• 计算机视觉
• 交通流预测
• 程序检测
• 解决图NP问题

将域知识结合进模型很重要，比如基于相对距离构建一个图可适用于交通流预测问题，但对于天气预测就不是很有效。
基于图的模型通常构建在其他体系结构之上，而不是独自工作。如何整合不同模型至关重要。

未来的方向：

• 不同类型的图。图数据的结构各异，现有的方法不能够适用于所有场景。大多数模型针对同质图，包含不同形态的异质图研究很少。标定图、超图等。
• 动态图。社交网络中，关系的建立于remove。
• 可解释性。
• 复合性

Zhang Z , Cui P , Zhu W . Deep Learning on Graphs: A Survey[J]. 2018.