【图像处理】数字图像傅里叶变换的物理意义及简单应用
【fishing-pan:https://blog.csdn.net/u013921430转载请注明出处】
前言
前面转载过一篇关于傅里叶变换原理的文章《一篇难得的关于傅里叶分析的好文》。那篇文章写得非常棒,浅显易懂,可以说稍有基础的人都能看懂那篇博文。但是那篇博文更多的是从信号处理的角度以及原理的角度讲述傅里叶变换。那么在数字图像处理中,傅里叶变换之后得到的频谱图又有怎样的运用呢?这篇博客就是为了简单讲讲傅里叶变换在数字图像处理中的意义和基本应用,如有错误请各位指出。
数字图像的傅里叶变换
通过前面的博文已经知道傅里叶变换是得到信号在频域的分布,数字图像也是一种信号,对它进行傅里叶变换得到的也是它的频谱数据。对于数字图像这种离散的信号,频率大小表示信号变化的剧烈程度或者说是信号变化的快慢。频率越大,变化越剧烈,频率越小,信号越平缓,对应到图像中,高频信号往往是图像中的边缘信号和噪声信号,而低频信号包含图像变化频繁的图像轮廓及背景等信号。
需要说明的是,傅里叶变换得到的频谱图上的点与原图像上的点之间不存在一一对应的关系。
频域数据的应用
1. 图像去噪
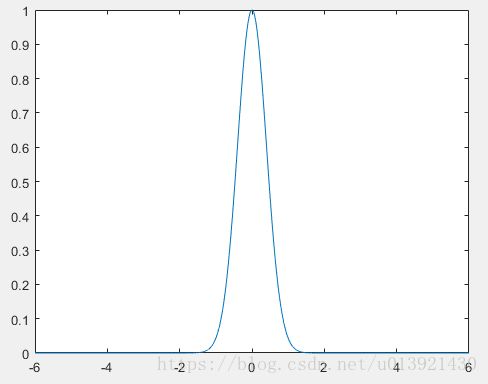
根据上面说到的关系,我们可以根据需要获得在频域对图像进行处理,比如在需要除去图像中的噪声时,我们可以设计一个低通滤波器,去掉图像中的高频噪声,但是往往也会抑制图像的边缘信号,这就是造成图像模糊的原因。以均值滤波为例,用均值模板与图像做卷积,大家都知道,在空间域做卷积,相当于在频域做乘积,而均值模板在频域是没有高频信号的,只有一个常量的分量,所以均值模板是对图像局部做低通滤波。除此之外,常见的高斯滤波也是一种低通滤波器,因为高斯函数经过傅里叶变换后,在频域的分布依然服从高斯分布,如下图所示。所以它对高频信号有很好的滤除效果。
高斯函数在频域的分布图像
2. 图像增强及锐化
图像增强需要增强图像的细节,而图像的细节往往就是图像中高频的部分,所以增强图像中的高频信号能够达到图像增强的目的。
同样的图像锐化的目的是使模糊的图像变得更加清晰,其主要方式是增强图像的边缘部分,其实就是增强图像中灰度变化剧烈的部分,所以通过增强图像中的高频信号能够增强图像边缘,从而达到图像锐化的目的。从这里可以看出,可以通过提取图像中的高频信号来得到图像的边缘和纹理信息。
3. 其他基于频谱和相位谱的操作等
下面我们通过代码来看一下是否真如我们想想的一样。
代码
clc;
clear all;
I=imread('lena.jpg');
I=rgb2gray(I);
%I=imnoise(I, 'gaussian', 0, 0.01); %%给图像添加高斯噪声;
subplot(231),imshow(I);
title('原图像');
s=fftshift(fft2(I)); %%低频部分移动到中心
% subplot(234),imshow(uint8(abs(s)),[]);
% title('图像傅里叶变换所得频谱');
subplot(234),imshow(log(abs(s)),[]);
title('图像傅里叶变换取对数所得频谱');
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
%%%%%%%低通滤波
d=min(a0,b0)/12; %滤波的范围,以频谱图上的欧氏距离为依据
Lp=zeros(a,b);
for i=1:a %设置低通滤波
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance<=d
h=1;
else
h=0;
end
Lp(i,j)=h*s(i,j);
end
end
subplot(235),imshow(log(abs(Lp)),[]);
title('低通滤波频谱');
LPJ=uint8(real(ifft2(ifftshift(Lp))));
subplot(232),imshow(LPJ);
title('低通滤波所得图像');
%%%%%%%高通滤波
d1=min(a0,b0)/12; %高通滤波的范围,以频谱图上的欧氏距离为依据
Hp=zeros(a,b);
for i=1:a %%设置高通滤波
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance>d1
h=1;
else
h=0;
end
Hp(i,j)=h*s(i,j);
end
end
subplot(236),imshow(log(abs(Hp)),[]);
title('高通滤波频谱');
HPJ=uint8(real(ifft2(ifftshift(Hp))));
subplot(233),imshow(HPJ);
title('高通滤波所得图像');
new=Hp.*1.5+Lp.*1;
NewIm=uint8(real(ifft2(ifftshift(new))));
figure,imshow(NewIm);
title('增强高频信号所得图像');运行结果
如果在图像中加入噪声,结果会如何呢?
结果分析
从上面的结果可以看出,低通滤波会让图像变得模糊,可以对图像进行模糊处理,滤除图像的噪声,高通滤波获得了图像的边缘和纹理信息。此外,通过增强图像的高频信号,可以增强图像的对比度,因为图像中的高频信号主要是出现在边缘及噪声这样的灰度出现跃变处的区域。
从频谱图上可以看出,当将频谱移频到原点以后,图像中心比较亮。在频谱图中,一个点的亮暗主要与包含这个频率的数目有关,也就是说在空间域中包含这种频率的点越多,频谱图中对应的频率的位置越亮。而经过频移后,频率为0的部分,也就是傅里叶变换所得到的常量分量在图像中心,由内往外扩散,点所代表的频率越来越高。可以从上面的结果中看出,只取核心的小范围内的低频信号再将其转换回到时域空间,已经能够在一定程度是看到图像的基本轮廓信息,这说明了图像中的“能量”主要集中在低频部分。
实际上,为了方便理解,可以把图像的二维傅里叶变换得到的频谱图看作图像的梯度分布图(两幅图像中的点并不是一一对应),频谱图中的某一个点所表征的是空间域中某一个点与周围点的灰度差异性,灰度差异越大,则频率越大。当然时域中灰度变化剧烈的区域也包含了低频信号,因为低频信号是构成图像信息的基础。
已完。。。