计算机的数学思想源头(回复“计算机数学”可下载PDF典藏版)
| 数据简化DataSimp导读:前篇《计算机诞生的详细历史》讲述古代算盘、机械计算机到现代计算机诞生的简史。本篇《计算机的数学思想源头》总结计算机诞生前7大数学思想源、诞生后5个现代几何学应用,约12种计算机的数学思想源头。读《逻辑的引擎》、《数学之美》、哈佛大学丘成桐CNCC2017演讲《现代几何学与计算机科学》、老顾谈几何、算法与数学之美读书笔记、数学理论科学家百度百科,发现用数学方法描述世界、解决问题,是大家的共同核心,是科学发展的核心动力。工程技术实现亦具有难度;而愚昧短视不开明环境,则限制了科学家的思考和研究,无情扼杀了很多科学思想。 目录 计算机的数学思想源头(20260字)1 01 计算机科学简史 (1228字)1 02 计算机的数学思想源头 (11436字)4 ▌1 [德]莱布尼茨的符号系统梦4 ▌2 [英]布尔把逻辑变成代数5 ▌3 [德]弗雷格发明形式句法7 ▌4 [德]康托尔对无限的探索8 ▌5 [德]大卫希尔伯特的营救9 ▌6 [捷克]哥德尔完备性定理10 ▌7 [英]图灵构想的通用计算机12 ▌8 第一批通用计算机的诞生13 ▌9 超越莱布尼茨智能之梦14 03 现代几何学在计算机科学5大领域的应用 (7322字)14 ▌1 现代几何的历史及几何学重要概念15 ▌2 几何学与计算机科学的相互影响16 ▌3 几何学在计算机科学的应用案例16 ▌4 总结与展望20 参考文献(506字)20
01 计算机科学简史 (1228字)计算机科学史简史A Brief History of Computer Science 在过去六十年左右的时间里,计算机已经从房间大小的巨型机器(megaboxes),转变成台式机(desktops)、笔记本电脑(laptops)到我们的口袋产品(pockets)。但是machine-assisted human computation机器辅助人类计算(“计算机”最初指的是某个人,不是某机器)的真正历史可追溯更早。这个星期是计算机科学教育周(Computer Science Education Week),为了庆祝世界科学节(the World Science Festival)开始,我们回顾一下人类最好的朋友——电脑的悠久历史。 历史记录中第一个计算器是算盘(abacus),它帮助古代技术人员获得了比贸易伙伴更多的优势,而贸易伙伴仍在手工计算奶牛(cows)和金龟子(amphorae双耳细颈椭圆土罐amphora名词复数)。
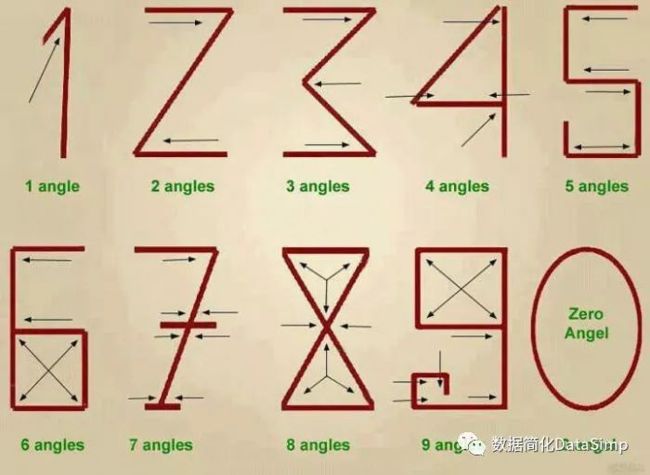
图1 数字最初是角的个数抽象出来的 已知最古老的复杂计算设备(complex computing device)是追溯到公元前87年(87 B.C),古希腊使用的一种称为“安蒂基西拉机器”(the Antikythera mechanism)的装置。据推测,希腊人使用这种齿轮操作的装置(gear-operated contraption,20世纪早期在爱琴海的一艘沉船中发现的,但直到2006才意识到它的意义)来计算天文位置(astronomical positions)、帮助他们在海洋中航行。 1843年的,计算又取得了一次飞跃。英国数学家爱达·勒芙蕾丝(Ada Lovelace)与查尔斯·巴贝奇(Charles Babbage他发明了第一台可编程计算机的理论。)合作,写了第一个计算机算法。 现代计算机时代(the modern computing-machine era)始于艾伦·图灵(Alan Turing)关于图灵机的概念(conception of the Turing Machine),三位贝尔实验室(Bell Labs)的科学家发明了晶体管(the transistor),使得现代计算成为可能,并使他们获得1956年诺贝尔物理学奖(the 1956 Nobel Prize in Physics)。几十年来,计算技术(computing technology)是政府和军方独有的;后来,学术机构上线,史蒂夫·沃兹尼亚克(Steve Wozniak)为苹果I型计算机(Apple-1)设计了电路板,使家用计算变得可行。 连接方面,提姆(=Timothy)·伯纳斯·李(Tim Berners-Lee)创建了万维网(the World Wide Web),马克·安瑞森(Marc Andreessen)创建了浏览器(a browse),这就给我们展示了一种生活在一个眼镜可以告诉我们所看到的东西的世界中。 随着可穿戴计算机(wearable computers)、可嵌入芯片(embeddable chips)、智能电器(smart appliances)以及其他正在进展和即将到来的进步,开发更智能、更快和更有能力的计算机的旅程显然才刚刚开始。 *文|世界科学基金World Science Foundation,作者:陈依莉和朱莉·罗斯曼Eli Chen and Julie Rossman。[1]
图2 文章配图Infographic:朱莉·罗斯曼Julie Rossman.[2] AI时代来临,在大多数研究者仍然没有掌握计算机设计制作技术精髓的情况下,很难相信如何跨过计算机科学“弯道超车”步入人工智能科学。我们必须了解这些过程,理解计算机、人工智能是如何诞生,背后的科学思想和原理是什么?加油!只会空想空谈喊口号表忠心可不行。(秦陇纪,2018) 在高等数学、离散数学、计算机基础等课程的学习中,我们已经了解到:莱布尼茨、乔治·布尔、康托、哥德尔、图灵、冯诺依曼等科学家。但死知识应试导向的教育教学中,我们的数学等学科太注重知识本身,而忽略了知识是如何被发现产生出来,以及不同的知识之间的渊源和启发关系。对于人类来说,文字知识是记录人类智能和思想的手段,而非终点。把文字考试作为教育目标,是极其简单粗暴、不负责任的。从启迪思想来说,应试是舍本逐末。这方面,愚昧落后的教育者要负愚民无耻的责任。
02 计算机的数学思想源头 (11436字)简化《逻辑的引擎》里数学理论科学家和百科人物介绍,在他们的时代被地主贵族资助、有一定自由做研究,其中涉及计算机诞生的思想。本文专注于理解这些与计算机诞生相关的伟大数学家及其数学思想,以及智能机器之梦怎样产生发展和解决问题的,我称之为计算机科学背后的数学基础。
▌1 [德]莱布尼茨的符号系统梦 戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz,1646年7月1日-1716年11月14日),德国哲学家、数学家,历史上少见的通才,被誉为十七世纪的亚里士多德。莱布尼茨在数学史和哲学史上都占有重要地位。在数学上,他和牛顿先后独立发明了微积分,而且他所使用的微积分的数学符号被更广泛的使用,莱布尼茨所发明的符号被普遍认为更综合,适用范围更加广泛。莱布尼茨还对二进制的发展做出了贡献。在哲学上,莱布尼茨的乐观主义最为著名;他认为“我们的宇宙,在某种意义上是上帝所创造的最好的一个”。他和笛卡尔、巴鲁赫·斯宾诺莎被认为是十七世纪三位最伟大的理性主义哲学家。莱布尼茨在哲学方面的工作在预见了现代逻辑学和分析哲学诞生的同时,也显然深受经院哲学传统的影响,更多地应用第一性原理或先验定义,而不是实验证据来推导以得到结论。莱布尼茨在政治学、法学、伦理学、神学、哲学、历史学、语言学诸多方向都留下了著作。[3]
1646年,莱布尼茨出生于德国莱比锡。10岁时学习了两千多年前亚里士多德提出的逻辑系统,唤醒他的数学兴趣。他对亚里士多德把概念分成固定的”范畴”着了迷,使他产生了一个伟大构想:将人类思维像代数运算那样符号化、规则化,从而让笨人通过掌握这样的规则变得聪明,更进一步制造出可以进行思维运算的机器,将人类从思考中解放。[4]莱布尼茨所确定的微积分符号在今天依然沿用,他对符号具有良好的感觉,通过选择良好的符号,可以大大的简化运算的复杂性。他满怀热情地指出发明“推理演算”和“逻辑代数”的重要性,甚至提出了“普遍文字”概念将文字运算变成一种“让我们算一下!”的过程。莱布尼茨为发展一种逻辑演算进行了很多尝试,得到的一些结果已经具有后来布尔的逻辑代数的雏形。 1673年,莱布尼茨在第一次访问伦敦时展示了一台能够执行四种算数基本运算的计算机模型,使得他被一致推选为伦敦皇家学会会员。在这之前,帕斯卡设计了一台能够进行加减运算的机器,但他的机器还能进行乘除运算,这是历史上第一次。这台机器包括了一个天才的部件——“莱布尼茨轮”,直到20世纪这个部件都在计算装置上普遍使用。1674年他又描述了一种能解代数方程的机器。[5] 他的目标,就是把推理归结为一种演算,并且制造出能够完成这些演算的机器。不幸的是,资助他的汉诺威公爵去世后,继任者要求他完成资助时陈诺的修订公爵家族史(好追溯到公元600年),而不是拿着资助到处拜访学者(期间在柏林建立了一个科学协会,后来成为科学院)。大科学家后30年基本陷入矿山挖矿、和牛顿派争斗等俗事废了。另外,他的博士论文首次被拒,在另一所大学通过。
▌2 [英]布尔把逻辑变成代数 乔治·布尔(George Boole,1815.11.2~1864),1815年11月2日生于英格兰的林肯,迫于家庭贫困15岁就去小学当老师、19岁自己在家乡办学校养家。担任15年校长后,直到科克城新成立大学给他提供教职,期间一直靠看书自学。他是19世纪最重要的数学家之一,出版《逻辑的数学分析》[6]是对符号逻辑诸多贡献中的第一次。1854年,他出版《思维规律的研究》[7],是他最著名的著作,书中布尔将逻辑代数化,介绍了现在以他的名字命名的布尔代数。[8]
19世纪,布尔发展出逻辑代数,成为后来计算机内部运算的逻辑理论基础。那时人们研究中认识到一种事实:代数的力量源于代表着量和运算的符号服从几条基本规则或定律。布尔早期著作开始思考,能否将逻辑推理也像代数那样用符号和几条基本规则就可以完全表达。 他开始思考我们通常所说的某物具有某种性质,可以用一个类来表示,比如白的是x,绵羊是y,那么白绵羊就可以用xy来表示,这样日常生活中的概念开始具有代数的形式,用现代的术语来说上面的xy表示的正是交集。他又继续思考,xx表示什么呢,他发现xx与我们普通的代数运算不同xx依然表示的是x。xx=x实际上成为布尔的逻辑代数的一个基本规则。 继续考虑下去,如果xx=x在普通的代数中意味着什么呢?xx=x,意味着x=1或者0.可以看到如果xx=x作为逻辑代数的基本规则,放在普通代数中意味着x=0或者1,那么逻辑代数是否意味着是01的普通代数呢。于是布尔得到一个基本原理,如果仅仅限于01,逻辑代数就变成了普通代数。关于这一点的思考,对于二进制运算的在逻辑代数中的主导作用具有很大的启发意义。 如果限于01,那么01在我们的逻辑代数中代表的意思又是什么呢。我们之前看到可以用x表示某个类,对应地那么0可以解释成没有任何东西属于它的类,1可以解释成包含所有对象的全体。同时布尔又开始考虑普通代数中的+-在逻辑代数中的意义,x+y可以表示具有x和y两种属性的对象集合,x-y表示具有x属性同时不具有y属性的对象集合。 考虑了这样的一些意义之后,接下来再看xx=x=> x-xx = 0 => x(1-x) = 0 现在我们以逻辑代数的观点看这个式子,它体现了这样一个含义:没有任何东西可以同时属于又不属于某个类。这点让布尔十分振奋,因为这刚好体现了亚里士多德的排中律,这就使他确信自己找对了路子。 继续下去,布尔发现三段论也可以用他的逻辑代数来表达。
图5 三种基本逻辑运算 所有x都是y x=xy(x中的任何东西也属于y,就等于说没有任何东西是属于x而不属于y的,也就是说x(1-y)=0) 所有y都是z y=yz ------------ ? 所有x都是z x=xz x=xy y=yz => x = xy = x(yz) = (xy)z = xz 最后,“如果x,那么y。”可以用x(1-y)=0来表示,可以这样理解这个式子意味着如果x=1,那么y=1。在这里一方面我们可以把“如果x,那么”理解为等同于前面的这样一句话“所有的x都是y”,当然这两者有一个区别,现在的x,y表示的是命题,而原来的x,y表示的则是类概念。以今天的观点来看,前者是命题演算,后者是谓词演算。 但是如果从另一个方面,重新考虑这句话,比如x=1表示命题x为真,x=0表示命题x为假,xy=1表示x且y,只有x,y均为1,xy=1,如果x=0或y=0,xy=0,这点又与普通代数相一致。从这个方向思考下去,就可以看到今天的布尔代数的基本面貌了,上面的这个定义正是与运算。 布尔的逻辑体系,不仅包含了亚里士多德的逻辑体系,而且还超越了它,但距离实现莱布尼茨之梦还是很远。其第一部关于逻辑是数学的革命性著作出版时,他才32岁。[9]但是仍有无法表达的情形:所有失败的学生或者是糊涂的或者是懒惰的。
图6 数学史上最伟大的三位数学家 今天的布尔代数 今天我们再看布尔再把逻辑转变成代数的过程中,所产生的逻辑代数在今天的计算机中扮演着什么样的作用。布尔代数只有1和0两个元素,not and or三种运算,用几张真值表就可以表达清楚。 AND | 1 0 -------------- 1 | 1 0 0 | 0 0 这张表说明如果AND运算的两个元素有一个是0,则运算结果总是0。如果两个元素都是1,运算结果是1。例如“太阳从西边升起”这个判断是假的(0),“水可以流动”这个判断是真的(1),那么“太阳从西边升起并且水可以流动”就是假的(0)。 OR | 1 0 -------------- 1 | 1 1 0 | 1 0 这张表说明如果OR运算的两个元素有一个是1,则运算结果总是1。如果两个元素都是0,运算结果是0。比如说“张三是比赛第一名”这个结论是假的(0),“李四是比赛第一名”是真的(1),那么“张三或者李四是第一名”就是真的(1)。 NOT | -------------- 1 | 0 0 | 1 这张表说明NOT运算把1变成0,把0变成1。比如,如果“象牙是白的”是真的(1),那么“象牙不是白的”必定是假的(0)。 如此简单的运算,当时的布尔不会想到它会被运用到计算机中,直到1938年香农在他的硕士论文中指出用布尔代数来实现开关电路,使得布尔代数成为数字电路的基础。所有的数学和逻辑运算,加、减、乘、除、乘方、开方等等,全部能转换成二值的布尔运算。[10]
▌3 [德]弗雷格发明形式句法 弗里德里希·路德维希·戈特洛布·弗雷格(德语:Friedrich Ludwig Gottlob Frege,1848年11月8日-1925年7月26日),德国数学家、逻辑学家和哲学家。他是数理逻辑和分析哲学的奠基人,一生主要发表了三本着作《概念演算--一种模仿算术语言构造的纯思维的符号语言》(1879)、《算术的基础--对数概念的逻辑数学研究》(1884)、《算术的基本规律》(l卷1893,2卷1903)。
代表作《概念演算》是本不到100页的小册子,将普通数学中的一切演绎推理都包含在内,成为第一个完备的逻辑体系,书名由2个德文词拼起来。布尔以普通代数为基础,用代数符号来表示逻辑关系。与此相反,弗雷格想以他的逻辑为基础而把代数构造出来。实际上这成为日后一个重要的学派“逻辑主义”,在他们看来逻辑与数学的关系就像一门学科的基本部分和高等部分之间的关系。 弗雷格的逻辑体系,表现在今天就是我们数理逻辑中的命题演算和谓词演算(用数学的方法研究关于推理、证明等问题的学科就叫做数理逻辑,也叫符号逻辑)。弗雷格第一次用精确的句法构造出形式化的人工语言,发明了形式句法,使得逻辑推理表示为机械演算即所谓的推理规则成为可能。概念文字亦是今天计算机程序设计语言的前身。秦陇纪提出文本数据简化,离不开形式句法工具。 弗雷格希望可以自然数提出一种纯粹逻辑的理论,从而证明算术、微积分乃至一切数学都可以看成逻辑的一个分支。于是弗雷格便希望可以用纯逻辑的术语来定义自然数,然后再用他的逻辑导出它们的性质。例如3这个数将被解释为逻辑的一部分。弗雷格的思想是把3定义为所有元素数为3的集合的集合。实际上这就是《算术的基础--对数概念的逻辑数学研究》这部著作的主要内容,是大突破。 但基于这样一些工作,1902年,年轻的伯特兰.罗素据此提出著名的罗素悖论:如果一个集合是它自身的一个成员,那么就把集合成为异常的,否则它就是正常的。那么由所有正常集合组成的集合是正常还是异常的呢?弗雷格的算术使用“集合的集合”这样一种概念。罗素指出,用集合的集合进行推理很容易导致矛盾,就是这样一种悖论。如果是正常的,那么它应该包含自身,这样它就应该是异常的。如果是异常的,那么它就不会包含自身,这样它就应该是正常的。无论哪个结果都导致了矛盾。实际上罗素构造这个悖论的方法,与之后哥德尔、图灵构造不可判定命题却有着神似的地方。这一矛盾表明弗雷格构造的算术体系所基于的那些前提是靠不住的,并给弗雷格带来了巨大的打击。 虽然弗雷格的逻辑已经很完备,但仍然具有一些局限性。他的规则并没有提供判定某个结论能否从给定的前提中推导出来的计算步骤。另外能否找到一种计算方法,它能够说明在弗雷格的逻辑中某一推理是正确的呢?其结果是这样一则证明:没有这样的一般方法存在。然而正是在证明这样一条否定性的结论过程中,阿兰·图灵发现原则上可以设计出一种通用机,它可以执行任何可能的计算。 弗雷格的研究开启语言哲学的大门,后来人们在寻找证明逻辑推理正确性的过程中,图灵发现了通用机,也就是今天计算机的数学模型。[11]
▌4 [德]康托尔对无限的探索 格奥尔格·康托尔(Cantor,Georg Ferdinand Ludwig Philipp,1845.3.3-1918.1.6)德国数学家,集合论的创始人。生于俄国列宁格勒(今俄罗斯圣彼得堡)。父亲是犹太血统的丹麦商人,母亲出身艺术世家。1856年全家迁居德国的法兰克福。先在一所中学,后在威斯巴登的一所大学预科学校学习。[12]
康托尔进入无限的世界,开始无限的数目的研究。他发现自然数与实数具有不同的基数,以及由此提出的连续统假设,即实数和自然数之间不存在具有其他基数的集合。这也是1900年,希尔伯特提出的23个问题中的第一问题。这个问题直到今天并未完全解决,1938年哥德尔和1963年保罗科恩的重大发现表明,如果连续统假设问题可以被解决,就必须超越普通数学的方法。 对于我们普通人来说,最有用的大概是康托尔在证明实数与自然数基数不同的过程中所采用的对角线方法,这种方法是1891年,康托尔在一篇4页的论文中发表的。对角线方法在以后的故事中仍被用到,它将被哥德尔用来解决一致性问题时构造系统内不可证命题,然后阿兰·图灵又再次使用了哥德尔的方法构造出了不可判定命题。而关于连续统假设的研究也引发了关于图灵机的构想。现在我们可以看到康托尔的工作与计算机的起源在这里产生了联系。 关于对角线方法,我们从自然数集来看,我们可以发现自然数与自然数的子集组成的集合之间具有不同的基数,假设我们把自然数与不同的自然数子集建立一个对应关系,1: M1 2: M2....,采用对角线方法,我们总是可以构造出一个新的自然数集,它没有任何自然数与之对应,我们这样产生这个新的自然数集:如果i属于Mi,那么排除i,否则包含i,容易看到这样产生的一个集合不同于任何的Mi。可见由一切自然数集组成的集合的基数要大于自然数的基数。 实际上康托尔并不是第一个关注到无限的数目特殊性的人,早在17世纪,莱布尼茨就发现偶数和自然数是一一对应的,正如他所说:对于任何一个数,都存在一个与之对应的偶数,那就是它的二倍。因此所有数的数目并不比偶数的数目更多,也就是说整体没有部分大。但是他得出了这样一个结论:所有自然数的数目这一概念是不一致的,讨论一个无限集中元素的数目是没有意义的。但是康托了选择了另一条路,他承认某些无限集将与它的一个子集具有相同的元素数目。正是基于这样一个大胆的选择,他才创立了关于无限的新理论。 康托尔提出这些观点之后,立刻引来各方面的责难。与弗雷格类似,人们发现用康托尔的超限数进行不加限制的推理会导致荒谬的结果。比如,如果存在一个由所有基数组成的集合,那么它的基数该是多少呢?它必须比所有基数都大,但一个基数又怎么可能比所有基数都大呢?后来罗素又指出这样的一个问题:是否存在一个所有集合的集合?如果存在,那么倘若把对角线方法应用于它,会出现什么结果?这样我们会得到一个不同于所有那些已经拥有标签的集合的集合。正在考虑这种情况时,罗素发现他那个关于由一切不是自身的集合组成的集合的著名悖论,也就是他向弗雷格传达的那个悖论。这里我们看到,弗雷格和康托尔之间被罗素悖论联系起来,使得弗雷格从突破到绝望。关于这个悖论的讨论和思考,则引发了数学史上的第三次危机。[13]
▌5 [德]大卫希尔伯特的营救 戴维·希尔伯特,又译大卫·希尔伯特,D.(David Hilbert,1862~1943),德国著名数学家。1900年8月8日巴黎第二届国际数学家大会上,他提出新世纪数学家应当努力解决的23个数学问题,被认为是20世纪数学的至高点,对这些问题的研究有力推动了20世纪数学的发展,在世界上产生了深远的影响。希尔伯特领导的数学学派是19世纪末20世纪初数学界的一面旗帜,希尔伯特被称为“数学界的无冕之王”,他是20世纪的数学领袖、天才中的天才。[14]
从莱布尼茨和牛顿创立微积分到大卫·希尔伯特成为数学家的两个世纪里,不少学者都发现极限过程可以漂亮地应用于许多方面。在这些结果中,很多是通过对符号的纯形式操作来获得的,人们对它们背后的含义未做过多考虑。1888年,希尔伯特游历德国各数学中心,同领域内主要人物接触,探讨了很多数学问题。之后,希尔伯特对“不变量之王”德国数学家果尔丹“关于代数不变量结构的简单化定理”问题的解决产生轰动而成为当时一流数学家。后来他的《数论报告》又诞生一大批成果。 1900年,希尔伯特在数学家大会指出的23个问题,第二个便是关于算术一致性的问题。即关于一个公理系统兼容性的问题,也就是判定一个公理系统内的所命题是彼此兼容无矛盾的,希尔伯特希望能以严谨的方式来证明任意公理系统内命题的兼容性。 希尔伯特纲领所提出的主要问题就是算术一致性问题。为了解决这个问题,希尔伯特发展出了元数学,一致性证明将在元数学内部完成。1928年,希尔伯特和他的学生阿克曼出版了一本逻辑课本,书中提出了关于弗雷格《概念文字》的基本逻辑(后来被称为一阶逻辑)两个主要问题:一个就是,证明一阶逻辑的完备性,即任何一个从外部看来有效的公式都可以只用课本里提出规则从系统内部导出;第二个问题,以希尔伯特的判定问题而闻名,即对于一个一阶逻辑的公式,如果找到一种方法,可以在定义明确有限步骤内判定这个公式是有效的。这两个问题分别为哥德尔和图灵解决,而在解决第二个问题的过程中,图灵提出了图灵机的概念。 后来在1928年的国际数学家大会上,希尔伯特又提出一个关于形式系统的问题,这个系统建立在把一阶逻辑应用于现在被称为皮亚诺算术或者PA的自然数公理系统的基础之上。希尔伯特希望可以证明PA是完备的,也就是说任何一个可以在PA中表出的命题或者可以在PA中被证明为真,或者可以被证明为假。两年后,这个问题被一个叫哥德尔的年轻人解决了,但答案却完全不像希尔伯特料想的那样。[15]
▌6 [捷克]哥德尔完备性定理 库尔特·哥德尔(Kurt Gödel)(1906年4月28日—1978年1月14日)生于捷克,卒于美国普林斯顿。他的是位数学家、逻辑学家和哲学家。其最杰出的贡献是哥德尔不完全性定理。1924年,库尔特在维也纳大学攻读物理,并参加哲学小组活动。1930年获博士学位。其博士论文证明了“狭谓词演算的有效公式皆可证”,之后在维也纳大学工作。1938年到美国普林斯顿高等研究院任职,1948年加入美国籍,1953年成为该所教授。哥德尔发展了冯·诺伊曼和伯奈斯等人的工作,其主要贡献在逻辑学和数学基础方面。[16]
希尔伯特在20世纪20年代介绍了他的元数学纲领:一致性有待证明的公理将被包含在一个形式逻辑系统之内,而证明仅仅是有限数目的符号的一种排列而已。当希尔伯特开始思考希尔伯特纲领时,希尔伯特的学生阿克曼和冯诺依曼似乎正在朝着用有限性方法证明PA的一致性的方向大步迈进。他们二人都已经为PA的一个有限的子系统找到了这样的证明,成功似乎指日可待。 这样哥德尔开始试图将算术一致性还原为PA的一致性,然而就是在这样的努力中失败了。哥德尔开始思考这些问题时,他重新思考了从外部而不是从内部考察一个系统的意思。从外部看,这些系统包含着符号串之间的关系。从内部看,这些系统能够表达关于不同数学对象的命题。哥德尔通过给符号串用自然数编码,将外部带到了内部。 哥德尔发现存在这样的命题,它们从系统外部看是真命题,但无法在系统内部得到证明。于是他得出了一个非凡结论:一种有意义的数学真理的观念不仅是存在的,而且其范围还超出了任何给定的形式系统的证明能力。在1931年,他发表论文《论 <数学原理>及有关系统的形式不可判定命题》中,他选择对形式系统PM给出了他的结果,从而说明即使强逻辑系统也不可能把全部数学真理包含在内。 在哥德尔的证明中,关键的一步在于他证明了:一个自然数作为PM中可证命题的一个代码,这一性质本身可以在PM中表示出来。根据这一事实,哥德尔可以在PM中构造出一些命题,这些命题可以被看做表达了这样一个断言,即某些命题在PM中是不可证的。也就是说他可以构造出一个命题A,该命题经译码后可以断言某一命题B在PM中是不可证的。现在,在没有获知密码的人看来,命题A不过是一串符号而已,但是通过代码,神秘性就消失了:A表示这样一个命题,即某个符号串B表示在PM中一个不可证的命题。A和B通常是不同的命题,哥德尔问,它们是否有可能是相同的呢?事实上它们可以是相同的,哥德尔可以利用对角线方法证明这个结论。 运用这些技巧,我们可以使被断言为不可证的命题和做出这一断言的命题是同一个命题。换句话说哥德尔发现了如果获得这样一个非凡的命题,我们将它称之外U,具有如下性质: U说某个特殊命题在PM中不可证。 那个特殊的命题就是U本身。 因此,U说“U在PM中不可证”。 如果我们承认PM中证明的任何命题都是真的,那么我们发现U是真的,但它在PM中不可证。 U是真的。假定它是假的,那么它表述的内容就是假的,因此它就是不是不可证的,而一定是可证的,从而是真的,这与开始假定U是假的矛盾,所以它一定是真的。因为它是真的,所以它表述的内容为真,所以它在PM中不可证。 我们把U称为不可判定命题,当然这种不可判断性只与系统内部的可证性,从我们外部的观点来看U是真的。 另一方面,在PM内部,我们可以证明:如果PM是一致的,那么U。因此正是PM是一致的这一个假定,才使U在PM内部得不到证明。既然我们知道U在PM内部是不可证的,我们就必须得出结论说,PM的一致性在PM中不可证。而希尔伯特的主要目的就在于:用于被认为构成PM的一个非常有限的子集的有限性方法来证明像PM这样的系统的一致性。然而哥德尔证明了,即使就PM的全部能力而言,它也不足以证明自身的一致性。于是希尔伯特纲领走到了尽头。[17]
图11 青年时期的库尔特·哥德尔Kurt Gödel与艾伦·麦席森·图灵Alan Mathison Turing
▌7 [英]图灵构想的通用计算机 艾伦·麦席森·图灵(Alan Mathison Turing,1912年6月23日-1954年6月7日),英国数学家、逻辑学家,被称为计算机科学之父,人工智能之父。1931年图灵进入剑桥大学国王学院,毕业后到美国普林斯顿大学攻读博士学位,第二次世界大战爆发后回到剑桥,后协助军方破解德国著名的密码系统Enigma帮助盟军取得了二战的胜利。图灵对于人工智能的发展有诸多贡献,提出了一种用于判定机器是否具有智能的试验方法,即图灵试验,至今,每年都有试验的比赛。此外,图灵提出的著名的图灵机模型为现代计算机的逻辑工作方式奠定了基础。[18] 2013年12月24日,英国司法部长克里斯·格雷灵(Chris Grayling)要求下,英国女王向图灵颁发了皇家赦免。英国司法部长宣布“图灵的晚年生活因为其同性取向(同性恋)而被迫蒙上了一层阴影,我们认为当时的判决是不公的,这种歧视现象现在也已经遭到了废除。为此,女王决定为这位伟人送上赦免,以此向其致敬。”[19]
1930年,哥德尓的博士论文中证明了弗雷格的规则是完备的,这样就回答了希尔伯特1928年提出的第一个问题。而第二个问题即判定问题,在哥德尔的工作发表之后,人们很难想象存在这样的判定算法,于是阿兰·图灵开始思考如果证明这样的算法是不存在的。 图灵采取了这样的一条道路,他首先分析了人的计算过程。通过丢掉非本质的细节,将这些计算活动局限在少数几种极为简单的基本操作上。(数据简化大法)然后图灵说明人可以被一个能够执行这些基本操作的机器所替代。然后只要证明仅仅执行那些基本操作的机器不可能判定一个给定的结论是否可以用弗雷格的规则从给定的前提中导出,这样他就能够下结论说,判定问题的算法是不存在的。 作为副产品,他对计算过程的分析,产生了通用计算机的一个数学模型。 他观察到:在计算的每一个阶段,只有少数符号受到了注意。每一个阶段所采取的行动仅仅取决于受到注意的那些符号以及当前的心灵状态。 然后他做出了如下抽象:计算通过在一条被划分成方格的纸带上写下符号来进行。执行计算的人在每一步都只注意其中一个方格的符号。她的下一步将仅仅取决于这个符号和她的心灵状态。她的下一步是这样的:她在当前注意的方格里写下一个符号,然后将注意力转向它左边或者右边的相邻符号。 现在可以很容易看出,做这项工作的人可以用一个机器替代,纸带在机器上来回移动。关键之处在于图灵对于计算概念的分析,通过某种算法程序可计算的任何东西都可以通过一台图灵机来计算。因此如果我们可以证明某些任务无法用图灵机完成,那么我们就可以说没有任何算法可以完成这项任务。这就是图灵证明判定问题不存在算法的方法。 实际上一台图灵机可以用这样的一个五元组来表示:当机器处于状态R,注视纸带上的符号a时,它将用b来代替a,向右移动一个方格,然后转到状态S。而一个具体的算法便可以由这些五元组表示的状态转换的集合组成的图灵机来表示出来。R a:b -> S 或者R a:b <-> 图灵将对角线方法应用于这种情况,得到了图灵机不能解决的问题,由此推出了判定问题的不可解性。与哥德尓类似,图灵采用了对角线方法也对图灵机通过自然数进行了编码。 图灵机本身可以是自然数编码表示,这样它也作为自身的输入。实际上有些输入会使图灵机停止下来,另一些则不会。这样一台图灵机就具有一些停机集合。如果我们考虑把一台图灵机的停机集合组成了一个包裹,并且认为那台机器的码数就是这个包裹的标签。对角线方法允许我们构造出一个与图灵机的任何停机集合都不同的自然数集合,我们称之为D。方法是这样的,我们考虑把图灵机的编码作为自身的输入,如果它的编码数不属于自身的停机集合,那么我们就把它加入D。而集合D则不是任何图灵机的停机集合。 然后考虑这样一个问题:找到一种算法,判定一个给定的自然数是否属于集合D。 这就是一个不可解问题的例子。首先如果存在这样的一个算法,我们就能找到这样的一个图灵机,但是我可以改造一下这个图灵机,把以下两个五元组加入到这个图灵机:F 0:口-> F 和 F 口:口-> F。对于这个新的改进的图灵机来说,如果输入的数属于D那么那么机器就会像以前一样运转,并输出1而告终,如果输入的数不属于D,那这台机器将永远向右移动。这样我们就找到了一台图灵机它的停机集合刚好就是D。于是与我们的对角线方法矛盾。所以并不存在这样的一个算法。由此可知判断问题在算法上是不可解的。 为验证自己工作的有效性,图灵又提出了通用机模型,通用机包含了图灵机代码以及待处理的数据。而这刚好对应着我们今天的机器,程序与数据的概念。也为存储程序计算机提供了一个模型。正是图灵在证明判定问题的不可解性是,对计算概念的分析以及对通用机的发现促使了计算机的产生。
▌8 第一批通用计算机的诞生 第二次世界大战结束时,英国国家物理实验所NPL大规模扩容,J R 沃玛斯莱(1907-1958)被任命为新的数学部门负责人。他意识到图灵1936年的早期论文“论可计算数”的实用含义。1938年,他承担了用电子继电器涉及一台通用计算机的任务,后来因为太慢放弃。1945年2月他去美国访问看到了ENIAC,得到一份冯诺依曼EDVAC报告,决定雇佣图灵。 1945年末,图灵完成了他著名的ACE(自动计算机)报告。ACE与EDVAC不同在于“后者是一份尚未完成的草案,重要的是它是不完整的。”而图灵的ACE是对计算机的一次完整描述,一直到逻辑电路图。也就是在这时冯诺依曼提出了他著名的“关于EDVAC的报告草案”,它实际上主张将要建造的EDVAC作为图灵通用机的一个物理模型实现出来。在这个报告里,提出了存储程序的概念,也就是沿用至今的冯诺依曼结构,实际上它的革命性不在于存储程序而是通用性,存储程序只是达到这一目的的一种手段。图灵ACE是与冯诺依曼EDVAC非常不同的机器,与两位数学家的不同态度密切相关。冯诺依曼希望EDVAC成为真正“通用的”,却把重点放在了数值计算。图灵发现ACE不适于做繁重的数学计算,更接近于论文《论可计算数》(图灵,1936)中的图灵机。由于图灵得不到英国经费支撑,战后ACE在NPL研制成功,被称为“Pilot ACE”。今天计算机RISC架构与ACE在哲学上是一致的。 1950年,图灵又发表了他的经典论文《计算机与智能》,提出了著名的图灵测试来测试计算机是否具有智能。1954年6月7日,图灵咬了一个浸过氰化物的苹果,结束了自己的生命。而他的通用机思想却延续到今天。[20]
图13 1980年UCB哲学家约翰·R·塞尔John R Searle的“中文屋”比喻
▌9 超越莱布尼茨智能之梦 把逻辑推理简化为形式规则的努力,可以追溯到亚里士多德。图灵的工作是莱布尼茨关于一种普遍的计算语言的梦想的根本基础。图灵说明了所有的计算都能够在他的通用机上完成,这一成就也是亚里士多德的工作为支撑的。计算和逻辑推理确实是同一个硬币的两面,利用这一洞见,我们不经可以为计算机编程,从而使其能够完成各种任务,而且还能设计研制一个物理模型实现出来。 1999年1月,美国科学促进会在加利福尼亚的阿纳海姆召开年会。会议主题“新世纪的挑战”,议程表有“逻辑在计算机科学中的非凡效力”专题讨论会。五位领衔计算机科学家(也是逻辑学家)在发言中写到:“过去25年,逻辑和计算机科学间发生了广泛而持续的相互作用,仍在不断加强。逻辑为计算机科学提供了一种统一的基础框架和建立模型的工具。逻辑在一些计算机科学领域,如人工智能、计算复杂性、分布式计算、数据库系统和设计验证等。”[21] 1940年代McCulloch和Pitts开始了以神经元作为逻辑器件的研究;1960年代Rosenblatt提出模拟学习和识别功能的“感知机”模型;1965年MIT计算机科学家约瑟夫·魏泽鲍姆Joseph Weizenbaum (8 January 1923–5 March 2008)的ELIZA对话程序;1996年IBM深蓝击败加里·卡斯帕罗夫;1980年UCB哲学家约翰·R·塞尔John R Searle的“中文屋”、“象棋屋”比喻;2016年Google旗下DeepMind公司研究员Dr.戴密斯·哈萨比斯(Demis Hassabis)团队的阿尔法围棋战胜人类…
图14 2016年3月Google研究员Dr.戴密斯·哈萨比斯Demis Hassabis团队的阿尔法围棋战胜人类 何时超越莱布尼茨之梦?放眼全书,至今为止,科研环境取决于政治制度,比如1928年德国大选后,很多数学家不允许授课,纷纷逃离德国。限定了思想意识必须是什么的国家,不可能有科学。 感谢纽约大学库郎数学研究所逻辑教授Dr.马丁·戴维斯Martin David Davis (born March 8, 1928)的科普力作《逻辑的引擎》,感谢译者,让我们了解计算机的数学思想源头。这些思想理论对文本做数据简化有启发吗?信息时代,知识爆炸,希望可以找到知识理论信息数据简化的方法。(秦陇纪,2018)
03 现代几何学在计算机科学5大领域的应用 (7322字)逻辑学对计算机科学起到推动和支撑作用,几何学为计算机科学发展起什么作用?现代几何为计算机科学的发展奠定了坚实的理论基础;计算机科学的发展为几何学提供了大量的研究素材,并且提供了高效精确的验证手段。现代几何的理论和方法日益渗透到计算机科学之中,并且通过计算机科学对人类社会做出更多的贡献。这里,我们给出一些现代几何理论在计算机科学中的直接应用。 一、在计算机网络领域:我们将黎曼几何的概念和方法推广到离散情形,在图上面定义曲率,并用曲率来刻画分析社交网络和互联网。我们运用共形几何的方法来提高无线传感器网络的路由性能,实现负载平衡。 二、在计算机图形学领域:我们用计算共形几何的方法实现曲面全局保角参数化,运用蒙日-安培方程来实现保面积参数化,用曲面曲率流来实现矢量场的设计。 三、在计算机辅助几何设计领域:我们用曲面的仿射结构、射影结构来构造整体光滑的样条曲面。 四、在数字几何处理领域:我们用黎曼映照和最优传输映射来做几何压缩,运用几何逼近论来做曲面重构。 五、在计算机视觉领域:我们用拟共形几何、Teichmuller理论来实现曲面配准,动态跟踪。我们用蒙日-安培理论来计算Wasserstein距离进行表情分类。 总之,数学是科学的基础工具,必须善于使用数学方法和工具。 丘成桐(Shing-Tung Yau),原籍广东省蕉岭县,1949年出生于广东汕头,同年随父母移居香港,美籍华人,哈佛大学终身教授,国际知名数学家。现任香港中文大学博文讲座教授兼数学科学研究所所长、清华大学丘成桐数学科学中心主任。[22]1969年毕业于香港中文大学崇基学院数学系,1971年获得加州大学伯克利分校数学博士(师从陈省身)[23-24];1993年被选为美国科学院院士,1994年成为台湾中央研究院院士和中国科学院外籍院士[25]。丘成桐证明了卡拉比猜想,以他的名字命名的卡拉比-丘流形是物理学中弦理论的基本概念,对微分几何和数学物理的发展做出了重要贡献。丘成桐囊括了菲尔兹奖(1982)、克拉福德奖(1994)、沃尔夫奖(2010)等奖项。特别是在1982年度荣获最高数学奖菲尔兹奖,是第一位获得这项被称为“数学界的诺贝尔奖”的华人,也是继陈省身后第二位获得沃尔夫数学奖的华人。[26] 丘成桐教授是当代最著名的数学家之一,他在中国计算机大会的特邀报告讲的是几何学对计算机科学(包括人工智能)的贡献,计算机领域的学者可从中受到启发。也许人们没有想过几何学对计算机科学的影响会如此之大,如果要更上一层楼,应该学习更高深的数学知识。 以下是丘成桐教授的演讲全文。 丘成桐:现代几何学在计算机科学中的应用 文|丘成桐,来源CCF数字图书馆CNCC>CNCC2017,2017-12-29
我很荣幸受邀来到中国计算机大会上演讲。我本人主要从事微分几何等基础数学领域的研究。但最近十多年来,因为我的学生,美国石溪大学顾险峰教授及其他朋友的缘故,我进行了一些与计算机科学有关的研究。通过研究我发现,纯数学尤其是几何学在计算机科学中大有作为。
▌1 现代几何的历史及几何学重要概念 现代几何的历史 在历史上,几何学是数学的开始。古希腊数学家欧几里得(Ευκλειδης)¹(公元前330~前275年)将平面几何的所有定理组合,发现这些定理都可以由五个公理推导出来,这是人类理性科学文明的重要里程碑之一。所以我也鼓励大家把这个方法运用到人工智能上——从复杂多样的网络中找到其最简单的公理。如果能够实现,将会是人工智能的里程碑! 当时希腊人的数学工具不够,除了二次方程定义的图形(直线、圆、平面、球等),没有能力处理更一般的图形。直到古希腊哲学家、数学家、物理学家阿基米德(Archimedes)²(公元前287~前212年)开始利用简单的微积分的无限算法计算体积,并开始发展射影几何理论。微积分的出现使得几何学进入了新纪元,微分几何由此诞生。几何学在瑞士数学家欧拉(Leonhard Euler)(公元1707~1783年)和德国数学家高斯(C.F.Gauss)(公元1777~1855年)手上突飞猛进,变分方法和组合方法被大量引用来描述几何现象和物理现象。 现代几何起源于德国数学家黎曼(Riemann)(公元1826~1866年)在1854年的博士论文,论文中首次将几何空间看成一个抽象而自足的空间,同时可以研究曲率和有关的几何问题。后来这个空间成为现代物理的基础,现在物理学中研究的引力波就是从这个空间开始的。没有这个空间,爱因斯坦(Albert Einstein)就不可能研究出广义相对论。黎曼的论文中认为离散空间也是一个重要的空间,它包含了我们现在研究的图论,或许可以用来研究宇宙万物可能产生的一切。因此,黎曼的这篇论文为现代几何奠定了基础,他的思想在现代几何学中具有不可替代的作用。150年后,我们还是看得到他的智慧。 附注:1.欧几里得(希腊文:Ευκλειδης,公元前330年~前275年),也被称为亚历山大里亚的欧几里得,以便区别于墨伽拉的欧几里得。古希腊数学家,被称为“几何学之父”。他活跃于托勒密一世(公元前323年~前283年)时期的亚历山大里亚,也是亚历山大学派的成员。他在著作《几何原本》中提出五大公设,成为欧洲数学的基础。欧几里得也写过一些关于透视、圆锥曲线、球面几何学及数论的作品。欧几里得几何被广泛认为是数学领域的经典之作。[27] 2.阿基米德(Archimedes,公元前287年~前212年),古希腊哲学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,享有“力学之父”的美称。阿基米德和高斯、牛顿并列为世界三大数学家。“给我一个支点,我就能撬起整个地球”是他的名言。[28] 对称 几何学能够提供很多重要的想法,其影响无所不在。其中一个重要的概念是“对称”。我们中国人讲的“阴阳”就是一个对称的例子。数学上有一个叫庞加莱对偶的概念,其实也是阴阳,但比阴阳更加具体。19世纪挪威数学家索菲斯·李(Sophus Lie)发展的李群,是物理学中的一个重要工具。现代物理中几乎没有一个学科可以离开李群。在几何学上,德国数学家克莱因(Klein)于1870年发表的《埃尔朗根纲领》中提出了用对称来统治几何的重要原理。随后,产生了许多重要的几何学分支,例如仿射几何、保角几何和投影几何等。这些几何都与图像处理有着密切的联系,近十多年来我们都是用保角几何等来处理各种图像问题。所以,当年被认为不重要的几何学,现在却有重要的实际用处。从大范围对称到小范围对称,都对20世纪的基础研究产生了重要的影响。 平行移动 另一个很重要的概念是平行移动。通俗地讲,平行移动就是空间中的一点与另外一点之间的一个比较的方法。这个概念在物理学和工程中已有广泛的应用,但至今还没有被引进到计算机科学中来。这是一个在数学中很重要、很广泛的概念,它影响了整个数学界两千年。所以,我期望平行移动能够在计算机科学中大放异彩。
▌2 几何学与计算机科学的相互影响 几何对于计算机科学的影响 现代几何为计算机科学奠定了理论基础,并且指导计算机科学未来的发展方向。 ●现代几何广泛应用于计算机科学几乎所有的分支,例如计算机图形学、计算机视觉和计算机辅助几何设计、计算机网络、数字几何处理、数字安全和医学图像等; ●黎曼几何有助于理解社交网络; ●现代几何理论有望用来理解人工智能的黑箱,例如深度学习、生成对抗网络和机器定理证明等; ●所有与图像或者网络有关的问题都是几何问题的一部分。 计算机科学对于几何的影响 计算机科学的发展为现代几何提供了需求和挑战,并推动了跨学科的发展。例如: ●人工智能中的机械定理证明推动了计算代数的发展; ●数据安全、比特币和区块链的发展推动了代数数论、椭圆曲线和模型式的发展; ●社交网络和大数据的发展,催生了持续同调理论的发展; ●动漫和游戏的发展推动了计算共形几何学科的诞生和发展; ●机器学习的发展推动了最优传输理论的发展。
▌3 几何学在计算机科学的应用案例 3.1图论 图论在计算机科学中的重要性是根本的。图由顶点和边组成,允许重边和过单顶点的圈。我们通过研究定义在顶点和边上的函数,就可以研究图的组合问题。例如,如何将原图分解成很多简单的子图,如何衡量各个分支间的连接度,如何将图染色等,这些问题都与图上的特征函数紧密相连。 事实上,图上的特征函数与光滑流形上的特征函数具有很多相似的地方。我们将四十年前我和郑绍远³、李伟光⁴所做的关于黎曼流形的特征函数的工作推广到图上,得到了很好的结果。图上的拉普拉斯算子自然定义了图上的取平均的操作,其特征根及其特征函数与图的组合函数密切相关。我们研究了图上的热扩散过程,发现运用李-丘估计能够控制热核。通过研究图上的薛定谔方程,定义了图上的量子隧道概念。这些概念都是从物理上来的,被借用到图上。我们将流形的拓扑结构推广到有向图上,定义了图上的同调群。同调群可以用来研究图上密切的关系和它的内容。 进化图论为表达种群结构提供了数学工具:顶点代表个体,边代表个体的交互作用。图可以用来代表各种具有空间结构的种群,例如细菌、动植物、组织结构、多细胞器官和社交网络。在进化过程中,每个个体依据自身的适应程度进行繁殖并侵占到邻近顶点。图的拓扑反映了基因的演化——变异和选择的平衡。特别地,互联网是一个非常复杂的网络。社交行为的进化可以用进化博弈论来研究。个体和邻居博弈,根据收益而繁殖。个体繁殖速率受到自身与其他个体的交互作用影响,从而产生进化博弈的动态演化。其核心问题在于,对于给定的图,如何决定哪种策略会取得成功。 2017年初,我们在Nature上发表了一篇文章⁵,得到了在任何给定的图上进行弱选择,自然选择从两种彼此竞争的策略中如何进行挑选的一个条件。这个理论框架适用于人类决策,也适用于任何集群组织的生态演化。我们从弱选择极限得到的结果,解释了何种组织结构导致何种行为。我们发现,如果存在成对的强纽带结构,合作就会大规模出现。我们用数学证明了社会学方面的一个结论:稳定的伙伴或者伴侣,对于形成合作型的社会起到了骨干作用。 附注:3.郑绍远,1970年毕业于香港中文大学联合书院数学系,师从国际著名数学家陈省身先生,在美国加州大学伯克利分校获得博士学位。后在普林斯顿大学、纽约州立大学石溪分校、加州大学洛杉矶分校等任教,之后在香港中文大学、香港科技大学数学系任系主任。他的卓越贡献是黎曼流形上的Laplacian特征值的比较定理。他与丘成桐教授合作解决了高级Minkowski问题,对Monge-Ampere方程、黎曼流形的特征值估计等方面作出了突出贡献。[29] 4.李伟光(Peter Li),美国加州大学尔湾分校数学系华裔教授,美国艺术和科学院院士。1982年丘成桐与李伟光合著的论文,给出了线性热方程的逐点微分不等式,在沿曲线积分后可以给出经典的Harnack不等式。被称为”李-丘”的工作所得到的Harnack不等式也是汉米尔顿(Hamilton)开创早先解决方案进行分析的基础。李伟光19岁赴美国求学,先后获得加州大学弗雷斯诺分校数学学士,加州大学伯克利分校数学硕士和博士学位。[30] 3.2计算机图形学:全局参数化 “基于共形几何的全局参数化”是我们研究了近20年的一个方向,自1999年顾险峰在哈佛大学读博士时就已经开始做这方面的工作了。曲面参数化问题就是如何将曲面整体光滑映射到二维参数区域,使得几何畸变最小。曲面参数化是纹理贴图和法向贴图等技术的基础。共形几何是从古典的黎曼几何中产生的一个很重要的几何分支。zz 我们将大卫雕像模型(如图16(a))共形(保角)地映射到平面上(如图16(b)),看上去似乎变化很大,其实不然,因为这是保持角度不变的。如果我们在参数区域平面上画好网格点,然后将这些网格点映射到人脸上,就能在人脸上显示出很漂亮的网格图形(如图16(c))。共形映射在工程中应用很广,因为它能将图上的无穷小圆仍然映射成无穷小圆,从而不会导致太大的变化。
图16 曲面的共形映射 上述应用中需要数学上一个很重要的定理,即庞加莱单值化定理。该定理是说映射的几何图形只与它的拓扑性有关,任何几何本质上可以归结为三种几何,即球面几何、欧氏几何、双曲几何。这样,我们就可以将很多很重要但又很复杂的几何用很简单的方式描述出来。 但保角映射也有其不足,所以我们发展了第二类映射——保面元映射。保面元映射能使面元的面积被保持,但角度不一定被保持。如图17所示,保角映射有可能将一个面拉得很远(如图17(b)),而保面元映射(如图17(c))则不会产生这种情况。根据凸几何中的闵可夫斯基定理和亚历山大定理,保面元映射可以通过求解蒙日-安培方程得到。
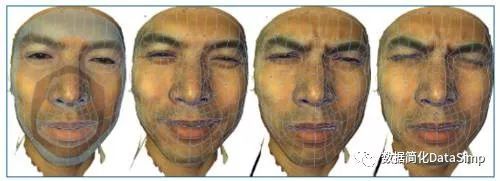
图17 曲面的保角映射和保面元映射 3.3计算机视觉:动态曲面追踪 计算机视觉中一个很重要的问题是动态曲面追踪(如图18),即给定一系列动态三维曲面,如何自动找到曲面间的光滑映射,使得特征点匹配,映射带来的几何畸变最小。共形映射也可以用来求解动态曲面追踪,并且应用到表情识别和追踪中,可以从一个人的各种面部表情得到他的重要面部特征。主要方法是用共形映射或保面元映射将它们映射到平面上,然后用拟共形映射来寻找最佳微分同胚。拟共形映射是一个很重要的数学工具,它在计算机数学上具有广泛应用。至今,数学家们仍在研究拟共形映射及其性质。它不是一个正则方程,而是一个伪正则方程,即Beltrami方程。在研究图形图像变形时这个方程非常重要,我们可以在微分同胚空间中进行变分,得到最优的映射。该方法在医疗和动漫中都有很重要的应用。
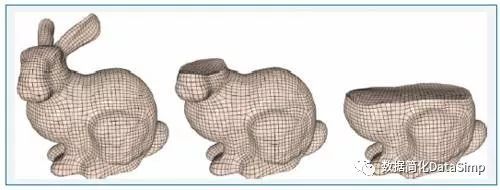
图18 动态曲面追踪 3.4计算力学:六面体网格生成 在计算力学中会经常用到六面体网格来进行有限元分析。我们也可以使用共形映射生成一个网格曲面的规则六面体网格,并且具有尽量少的奇异点和奇异线。图19是在一只兔子模型内部生成了比较好的六面体网格。根据拓扑学理论,生成六面体网格时通常会产生一些奇异点。基于叶状结构理论,我们对这些奇异点进行分类,并进行了一些深入研究,从而得出了一些在计算机科学上有意义的结论。
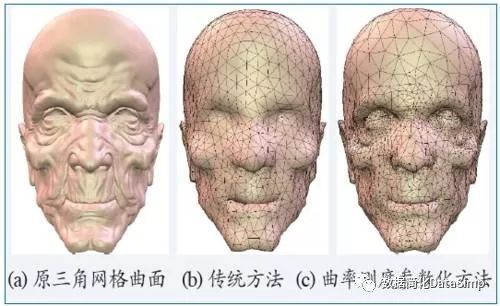
图19 兔子曲面的六面体网格生成 3.5数字几何处理:几何压缩 数字几何处理中一个很重要的问题是几何压缩。在进行几何压缩时需要用到蒙日-安培理论和几何逼近理论。如何压缩复杂几何数据,保证几何误差最小,并同时保证黎曼度量、曲率测度和微分算子的收敛性,这就是几何压缩问题。我们采取的解决方法是用共形映射将曲面映射到平面,再用蒙日-安培理论,将高曲率区域放大,然后重新采样,并在共形参数域上进行Delaunay三角剖分。这样得到的简化多面体网格就能够保证黎曼度量、曲率测度和微分算子收敛。采用不同的几何压缩方法将图20(a)所示的三角网格压缩到4000个顶点所得的结果如图20(b)和图20(c)所示。
图20 不同的几何压缩方法对比 3.6人工智能 机器学习算法需要大量的有标注的样本数据。对于图像分类,经常需要使用上千万张有标注的图像来进行训练。对于语音识别,需要成千上万小时有标注的语音数据。对于机器翻译,通常是在千万量级的双语语对上进行训练。但是很多领域却无法收集大数据,一是因为实例过少,例如医疗方面的疑难杂症;二是由于过于抽象,例如几何研究中的高维流形等。 机器学习算法中的深度神经网络需要数十亿个参数,需要昂贵的硬件支持和漫长的计算时间,训练难度很大。机器学习算法等价于能量优化。由于规模庞大,无法用二阶优化,因而一般是用随机梯度下降法。由于深度神经网络层数过深,经常出现梯度消失和梯度爆炸问题,因此训练过程收敛困难。 目前,以神经网络为代表的统计机器学习在工程实践中取得了成功,但是其理论基础非常薄弱,被人们称为黑箱算法。人工智能算法的不可解释性,极大地阻碍了这一领域的进一步应用和发展。深度学习理论的建立,应该是目前最为迫切的问题。 人类的智能主要包括归纳总结和逻辑演绎,对应着人工智能中的联结主义(如人工神经网络)和符号主义(如Groebner Basis方法)。人类对大量的视觉听觉信号的感知处理都是下意识的,是基于大脑皮层神经网络的学习方法;大量的数学推导和定理证明是有强烈主观意识的,是基于公理系统的符号演算方法。 虽然人工智能的算法原理目前没有被透彻理解,但我们相信其内在原理可以用现代几何原理来解释。例如,对于机器定理的证明,我们运用了希尔伯特定理;对于生成对抗网络,我们运用了亚历山大定理和蒙日-安培方程。 人工智能中,符号主义的一个代表就是机器定理证明。目前基于符号计算的机器定理证明的理论根基是希尔伯特定理:多元多项式环中的理想都是有限生成的。首先,我们将一个几何命题的条件转换成代数多项式,同时把结论也转换成多项式,然后证明条件多项式生成的根理想包含结论对应的多项式,即将定理证明转化为根理想成员判定问题。一般而言,多项式理想的基底并不唯一,Groebner基方法可以生成满足特定条件的理想基底,因此可以自动判定理想成员问题。从计算角度而言,Groebner基方法所要解决的问题的本质复杂度都是超指数级别的,所以即便对于简单的几何命题,其机器证明过程都可能引发储存空间的指数爆炸,这揭示了机器定理证明的本质难度。到目前为止,机器定理证明方法还没有发现深刻的定理。 生成对抗网络是联结主义的一个例子。生成对抗网络其实就是以己之矛克己之盾,在矛盾中发展,使得矛更加锋利,盾更加强韧。这里的盾被称为判别器,矛被称为生成器。通常生成器G将一个随机变量(例如高斯分布或者均匀分布),通过参数化的概率生成模型(通常是用一个深度神经网进行参数化)进行概率分布的逆变换采样,从而得到一个生成的概率分布。判别器D通常也采用深度卷积神经网络。例如,给定两个概率分布μ和v,其中μ是随机白噪声,v是人脸相片的概率分布。这样,生成对抗网络问题就是在两个概率分布μ和v之间找到一个最优传输映射(见图21)。我们可以通过对蒙日-安培方程进行求解来找到最优传输映射,从而节省很多生成对抗的时间。蒙日-安培方程本身就等价于微分几何中的亚历山大定理。
图21 生成模型 生成对抗网络实质上是用深度神经网络来计算概率测度之间的变换。虽然规模宏大,但是数学本质并不复杂。应用相对成熟的最优传输理论和蒙日-安培理论,我们可以为机器学习的黑箱给出透明的几何解释,这有助于设计出更为高效和可靠的计算方法。
▌4 总结与展望 现代数学和计算机科学的发展紧密相关。共形几何的单值化定理、蒙日-安培理论、最优传输理论、凸几何的Minkowski-Alexandrov理论等现代几何中的深刻定理,已经应用到计算机科学的许多领域。特别地,数字金融中的区块链技术依赖于数论的现代成果,人工智能的理论解释依赖于现代代数中的希尔伯特理论等。 希望我们能够将更多的数学理论应用到计算机科学中,不仅能有效地提出各种计算机算法,而且能给出理论的基础。人工智能需要一个坚实的理论基础,否则它的发展会有很大困难。我们期待计算机科学与现代几何能有更为深刻和密切的结合,更多的跨学科领域被创立、成长和壮大。我们相信人工智能的理论基础,深度学习的几何解释和数字金融的理论近期会得到蓬勃发展! -END-
参考文献(506字) 1-5. 百度.世界上最早的计算机.[EB/OL] https://zhidao.baidu.com/question/373378024.html,2018-03-30. 6-10. 知乎.最早的计算机是怎么来的?.[EB/OL] https://www.zhihu.com/question/20834957,2016-05-26. 11-15. CSDN.IT历史:计算机业简史.[EB/OL] https://blog.csdn.net/ecrown/article/details/249751,2015-01-12. 16-19. 学习百眼通.重温历史——计算机简史.[EB/OL] http://www.360doc.com/content/14/0801/20/17799864_398690110.shtml,2014-08-01. 20. Eli Chen and Julie Rossman.A Brief History of Computer Science.[EB/OL] https://www.worldsciencefestival.com/infographics/a_history_of_computer_science/,2013-12-0. 21. Integrated Algebra Just another CCSD Blog Sites site.Algebra Regents Exam Wednesday June 17, 2015.[EB/OL] http://blogs.ccsd.edu/arenholz/,2015-06-08. 22. [美]马丁·戴维斯.逻辑的引擎.湖南科学技术出版社:2012-04-11. 23. 吴军.算法之美.清华大学出版社:2018-04-11. 24. Allen B,Lippner G,Chen Y T,et al.Evolutionary dynamics on any population structure[J].Nature,2017,544(7649):227. 25. math absent.The Logic Behind Numbers publish in Images on June 2nd, 2013.[EB/OL] http://www.myconfinedspace.com/2013/06/02/the-logic-behind-numbers/,2013-06-02. 26. Isha USA.Day–Quality of a Leader by Isha USA.[EB/OL] http://www.ishafoundation.org/us/blog/presidents-day-quality-leader/,2015-02-15. 27. 老顾谈几何.纽约州立大学石溪分校计算机系终身教授:顾险峰——技术爆炸的亲历观察.[EB/OL] https://mp.weixin.qq.com/s?__biz=MzIyMzk1MDE3Nw==&mid=2247493150&idx=1&sn=4ef54c4b6f3c389663d8f4e940fb3e83,2018-03-19. 28. 百度百科.丘成桐.[EB/OL] https://baike.baidu.com/item/%E4%B8%98%E6%88%90%E6%A1%90,2018-01-07. 29. 发烧刚好辅导班.《逻辑的引擎》读后感.[EB/OL] https://wenku.baidu.com/view/b5bfe9674a73f242336c1eb91a37f111f0850d43.html,2017-11-17. 30. 数学英才转载.计算机起源的数学思想.[EB/OL] https://mp.weixin.qq.com/s?__biz=MzAwMzU4MjQxNg==&mid=2650909795&idx=1&sn=f98a17aad87a888f77b902fdae1ca38a,2018-04-11. 31. 算法与数学之美.计算机起源的数学思想.[EB/OL] http://www.sohu.com/a/225647866_701814,2018-03-15. 32. QQ快报转.CCCF“CNCC2017特邀报告”丘成桐:现代几何学与计算机科学.[EB/OL] http://www.xue63.com/toutiaojy/20171218B0I22W00.html,2017-12-18. 33. CCF整理.CCCF“CNCC2017特邀报告”丘成桐:现代几何学与计算机科学.[EB/OL] http://www.ccf.org.cn/c/2017-12-29/621495.shtml,2017-12-29. |