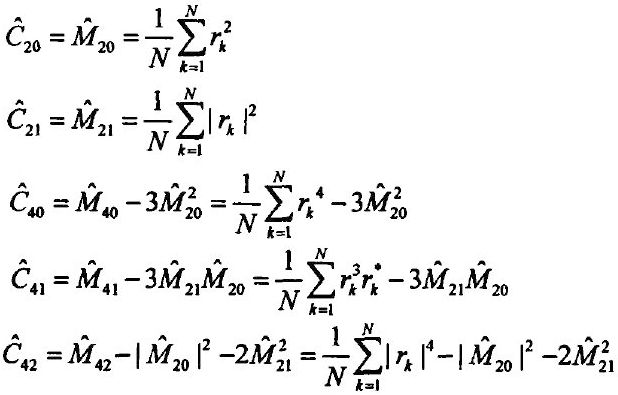Matlab实现加性高斯白噪声信道(AWGN)下的digital调制格式识别分类
内容大纲
加性高斯白噪声信道(AWGN)下的digital调制格式识别分类
(1. PSK; 2. QPSK; 3.8QAM; 4. 16QAM; 5. 32QAM; 6.64QAM)
100次独立仿真,识别正确率 vs SNR
设计
我的实现方法是 基于高阶累积量的信号特征的识别算法
调制格式识别过程如下:
信号预处理
- 去除直流成分
信号在接收端由于接收机的影响,有可能产生直流成分。直流分量在后面混频等处理中会产生影响,因此在信号处理以前必须去除直流成分。
令s ̅(t)表示信号s(t)的均值,即
则去除直流后的信号表示为
%去除直流成分
CMAOUT = CMAOUT - mean(CMAOUT);- 信号功率归一化
由于信道衰落影响到接收信号的功率,提取有关幅度的特征参量时会出现不一致的情况。因此需要对接收信号进行功率归一化,以消除信号功率的影响。令σ_x^2表示已经经过去除直流分量之后的信号x(t)的平均功率,即
![]()
那么经过功率归一化后的信号表示为
%normalization接收信号功率归一化
CMAOUT=CMAOUT/sqrt(mean(abs(CMAOUT).^2));特征提取
基于高阶累积量的信号处理方法,对通信信号中的加性高斯噪声有很好的抑制能力,在低信噪比下进行信号识别也能有良好的性能,应用在信号分析领域是非常有效的。
随机过程的k阶累积量为
![]()
则根据定义,随机过程的二阶和四阶累积量为
如果定义![]()
,令![]()
,则上面累积量的表达式化简为:
在信号的实际处理中,要从有限的接收数据中估计信号的累积量,可以采用采样点的平均代替理论的平均。例如,给定观察数据r_k,k=1,2,⋯,N,则可以使用下来的估计表达式。当信号和噪声的8阶矩存在并为有限值的时候,其不同定义的4阶累积量的估计是渐进无偏的一致估计。
由于处理的信号是在AWGN信道下接收的,所以对于C21这个二阶累积量来说,由于是信号模的平方近似计算得到的,因此噪声的功率会也包含进去了。所以,需要处理C21这个累积量。由于信噪比已知,则可以计算信号功率根据信噪比关系求得噪声功率。
令snr为信噪比,则
C21的累积量的更新为
C21=C21-noise_power
s = CMAOUT;
signalpow = mean(abs(s).^2);%信号功率
noisepow = signalpow/(10^(snr(snrIndex)/10));%噪声功率
C20_hat = mean(s.^2);
C21_hat = mean(abs(s).^2);
C21_hat = C21_hat-noisepow;%计算信号二阶累积量C21时,由于C21为信号模的平方
%而我们接收的s是在AWGN信道下接收的,所以求C21时还应考虑噪声功率。
C40_hat = mean(s.^4)-3*C20_hat^2;
%C41_hat = mean((s.^3).*conj(s))-3*C20_hat*C21_hat;
C42_hat = mean(abs(s).^4)-abs(C20_hat)^2-2*C21_hat^2;
C40_normal = C40_hat/C21_hat.^2;
%C42_normal = C42_hat/C21_hat.^2;分类识别
从论文中得知的一些四阶累积量的性质:
但是,对于实际接收到的信号,由于信号功率的影响,无法从累积量的绝对值中进行信号的区分。为了能够各阶累积量相比较,必须采取将信号功率归一化的方法,使得不同信号的累积量具有可比性。归一化是假设信号具有单位功率,即C_21=1,其他四阶累积量利用C_21进行归一化:
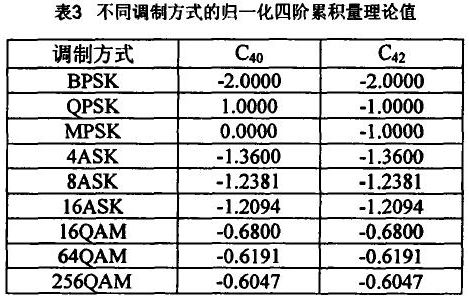
查询可得不同调制方式的归一化四阶累积量理论值
根据以上表格内容可以做出判断
AbsC40 = abs(C40_normal);
if(j==printJ) fprintf('%g ',AbsC40); end
if(AbsC40>=1.5)%PSK
classify = 1;
elseif(AbsC40>=0.9&&AbsC40<1.1)%QPSK
classify = 2;
elseif(AbsC40>=1.1&&AbsC40<1.3)%8QAM
classify = 3;
elseif(AbsC40>=0.67&&AbsC40<0.9)%16QAM
classify = 4;
elseif(AbsC40<0.35)%32QAM
classify = 5;
elseif(AbsC40>=0.35&&AbsC40<0.63)%64QAM
classify = 6;
end
if(classify == System.BitPerSymbol)
classify_correct = classify_correct + 1;
end最后打印出信噪比与识别正确率的关系和对应的星座图
classify_correct_ratio(snrIndex) = classify_correct/ClassifySetNumber*100;
end
%%绘制图形
figure(1);subplot(2, 3, j);
plot(snr, classify_correct_ratio, '-b.');
figure(2);subplot(2, 3, j);
plot(real(CMAOUT),imag(CMAOUT),'.'); 运行效果
实验中用到的参数设置
%%参数设置
snr_mini = 5; %信噪比最小值
snr_max = 20; %信噪比最大值
TxSampleRate = 32e9; %信号的码元速率
TxLinewidth = 0; %发射信号的载波线宽
TxCarrierRate = 0; %发射信号的载波频率
DataSymbolNumber = 10000; %数据点的个数
ClassifySetNumber = 100; %独立仿真的次数
printJ = 5; %需要输出观察的调制方式,0为不输出
printXingZuo = 1; %是否需要打印星座图,0为不打印
% signal generation;如果想要进行100组独立的测试,可以建立100次循环,产生100组独立的数据
for j = 1:6 % bit per symbol: 1. PSK; 2. QPSK; 3.8QAM; 4. 16QAM; 5. 32QAM; 6.64QAM...
System.BitPerSymbol = j;
snr = snr_mini:snr_max; %SNR信噪比的设置,单位dB
classify_correct_ratio = zeros(length(snr), 1);
for snrIndex= 1:length(snr)
if(j==printJ) fprintf('\n--------------- snr = %d ------------\n',snr(snrIndex)); end
classify_correct = 0;
for i = 1:ClassifySetNumber
Tx.SampleRate = TxSampleRate; %symbol Rate,信号的码元速率,可以自行定义
Tx.Linewidth = TxLinewidth;%发射信号的载波的线宽,一般与信号的相位噪声有关
Tx.Carrier = DataSymbolNumber;%发射信号的载波频率
M = 2^System.BitPerSymbol;从上述可以看出,一共进行了100次独立仿真。
由于没有找到32QAM的累积量的理论值,但是通过实验探究可以观察在32QAM的调制方式下。
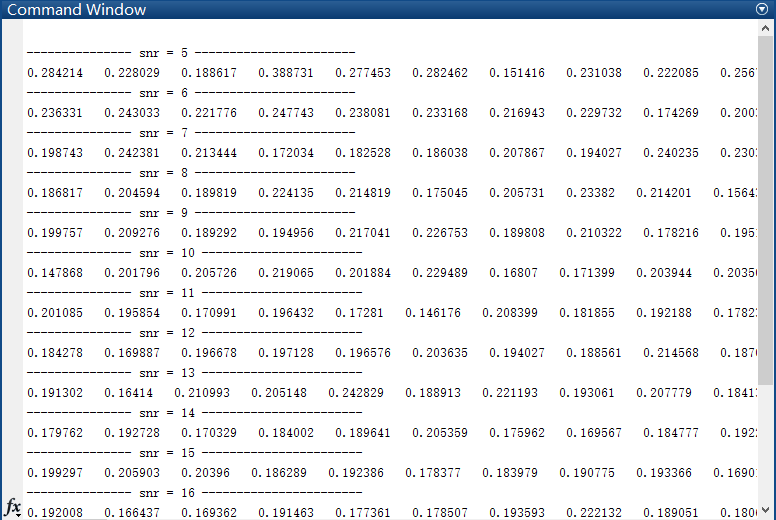
通过输出语句我们可以观察到如下
当信噪比在不同的取值情况下面,由于归一化处理,32QAM的C40的模值的理论值应为0.2
在不同的信噪比下面,识别正确率如下图:
要求的信噪比是12—15,在信噪比的比较低的时候,识别会有一定的误差,例如信噪比只有5的情况下比较明显,随着信噪比的提升,噪声的影响减少,分类识别的方法体现出来良好的稳定性。可以看到,信噪比大于10之后的识别率几乎都达到了100%。其中PSK的识别率是最好的。64QAM在累积量的识别方法里面低信噪比时稍微差点。
对应的调制方式星座图如下:
其中64QAM的区分没有特别明显,这就是低信噪比时产生的识别困难情况。但是稍微提高信噪比就能很好的识别。
完整代码
clear all;
clc;
%%参数设置
snr_mini = 5; %信噪比最小值
snr_max = 20; %信噪比最大值
TxSampleRate = 32e9; %信号的码元速率
TxLinewidth = 0; %发射信号的载波线宽
TxCarrierRate = 0; %发射信号的载波频率
DataSymbolNumber = 10000; %数据点的个数
ClassifySetNumber = 100; %独立仿真的次数
printJ = 5; %需要输出观察的调制方式,0为不输出
printXingZuo = 1; %是否需要打印星座图,0为不打印
% signal generation;如果想要进行100组独立的测试,可以建立100次循环,产生100组独立的数据
for j = 1:6 % bit per symbol: 1. PSK; 2. QPSK; 3.8QAM; 4. 16QAM; 5. 32QAM; 6.64QAM...
System.BitPerSymbol = j;
snr = snr_mini:snr_max; %SNR信噪比的设置,单位dB
classify_correct_ratio = zeros(length(snr), 1);
for snrIndex= 1:length(snr)
if(j==printJ) fprintf('\n--------------- snr = %d ------------\n',snr(snrIndex)); end
classify_correct = 0;
for i = 1:ClassifySetNumber
Tx.SampleRate = TxSampleRate; %symbol Rate,信号的码元速率,可以自行定义
Tx.Linewidth = TxLinewidth;%发射信号的载波的线宽,一般与信号的相位噪声有关
Tx.Carrier = DataSymbolNumber;%发射信号的载波频率
M = 2^System.BitPerSymbol;
%%信号生成
Tx.DataSymbol = randi([0 M-1],1,DataSymbolNumber);%每一次随机产生的数据量
%数据的不同调制方式产生:这里把2^3(8QAM)的形式单独拿出来设置,是为了实现最优的星型8QAM星座图
if M ~= 8;
h = modem.qammod('M', M, 'SymbolOrder', 'Gray');
Tx.DataConstel = modulate(h,Tx.DataSymbol);
else
tmp = Tx.DataSymbol;
tmp2 = zeros(1,length(Tx.DataSymbol));
for kk = 1:length(Tx.DataSymbol)
switch tmp(kk)
case 0
tmp2(kk) = 1 + 1i;
case 1
tmp2(kk) = -1 + 1i;
case 2
tmp2(kk) = -1 - 1i;
case 3
tmp2(kk) = 1 - 1i;
case 4
tmp2(kk) = 1+sqrt(3);
case 5
tmp2(kk) = 0 + 1i .* (1+sqrt(3));
case 6
tmp2(kk) = 0 - 1i .* (1+sqrt(3));
case 7
tmp2(kk) = -1-sqrt(3);
end
end
Tx.DataConstel = tmp2;
clear tmp tmp2;
end
Tx.Signal = Tx.DataConstel;
%数据的载波加载,考虑到相位噪声等
N = length(Tx.Signal);
dt = 1/Tx.SampleRate;
t = dt*(0:N-1);
Phase1 = [0, cumsum(normrnd(0,sqrt(2*pi*Tx.Linewidth/(Tx.SampleRate)), 1, N-1))];
carrier1 = exp(1i*(2*pi*t*Tx.Carrier + Phase1));
Tx.Signal = Tx.Signal.*carrier1;
Rx.Signal = awgn(Tx.Signal,snr(snrIndex),'measured');%数据在AWGN信道下的接收
%%信号识别
CMAOUT = Rx.Signal;
%去除直流成分
CMAOUT = CMAOUT - mean(CMAOUT);
%normalization接收信号功率归一化
CMAOUT=CMAOUT/sqrt(mean(abs(CMAOUT).^2));
s = CMAOUT;
signalpow = mean(abs(s).^2);%信号功率
noisepow = signalpow/(10^(snr(snrIndex)/10));%噪声功率
C20_hat = mean(s.^2);
C21_hat = mean(abs(s).^2);
C21_hat = C21_hat-noisepow;%计算信号二阶累积量C21时,由于C21为信号模的平方
%而我们接收的s是在AWGN信道下接收的,所以求C21时还应考虑噪声功率。
C40_hat = mean(s.^4)-3*C20_hat^2;
%C41_hat = mean((s.^3).*conj(s))-3*C20_hat*C21_hat;
C42_hat = mean(abs(s).^4)-abs(C20_hat)^2-2*C21_hat^2;
C40_normal = C40_hat/C21_hat.^2;
%C42_normal = C42_hat/C21_hat.^2;
AbsC40 = abs(C40_normal);
if(j==printJ) fprintf('%g ',AbsC40); end
if(AbsC40>=1.5)%PSK
classify = 1;
elseif(AbsC40>=0.9&&AbsC40<1.1)%QPSK
classify = 2;
elseif(AbsC40>=1.1&&AbsC40<1.3)%8QAM
classify = 3;
elseif(AbsC40>=0.67&&AbsC40<0.9)%16QAM
classify = 4;
elseif(AbsC40<0.35)%32QAM
classify = 5;
elseif(AbsC40>=0.35&&AbsC40<0.63)%64QAM
classify = 6;
end
if(classify == System.BitPerSymbol)
classify_correct = classify_correct + 1;
end
%subplot(1,7,snrIndex);%绘制原始噪声
%plot(Rx.Signal,'.');
%plot(CMAOUT,'.');
end
classify_correct_ratio(snrIndex) = classify_correct/ClassifySetNumber*100;
end
%%绘制图形
figure(1);subplot(2, 3, j);
plot(snr, classify_correct_ratio, '-b.');
axis([snr_mini snr_max 0 110]);
ylabel('识别正确率/%');
xlabel('信噪比/dB');
if(j == 1)
title('PSK调制方式识别');
elseif(j == 2)
title('QPSK调制方式识别');
elseif(j == 3)
title('8QAM调制方式识别');
elseif(j == 4)
title('16QAM调制方式识别');
elseif(j == 5)
title('32QAM调制方式识别');
else
title('64QAM调制方式识别');
end
if(printXingZuo==1)
figure(2);subplot(2, 3, j);
plot(real(CMAOUT),imag(CMAOUT),'.');
if(j == 1)
title('PSK调制方式星座图');
elseif(j == 2)
title('QPSK调制方式星座图');
elseif(j == 3)
title('8QAM调制方式星座图');
elseif(j == 4)
title('16QAM调制方式星座图');
elseif(j == 5)
title('32QAM调制方式星座图');
else
title('64QAM调制方式星座图');
end
end
end