协方差自适应调整的进化策略(CMA-ES)转载自知乎
因为毕设原因需要学习CMA-ES算法,放在自己的博客留作学习,内容转载自:https://zhuanlan.zhihu.com/p/31193293
本文仅作个人学习用,若有侵权请联系删除
协方差自适应调整的进化策略(Covariance Matrix Adaptation Evolution Strategy, CMA-ES)是最有名,应用最多,性能最好的ES之一,在中等规模(变量个数大约在 3-300范围内)的复杂优化问题上具有很好的效果。是Google Vizier: A Service for Black-Box Optimization 包含的四种用于调hyper-parameter 的方法之一。
按照惯例,先列举几个应用文章:
Path Integral Policy Improvement with Covariance Matrix Adaptation, ICML, 2012.
Optimizing Walking Controllers for Uncertain Inputs and Environments, ACM Transactions on Graphics 29. 4 (2010)
Flexible Muscle-Based Locomotion for Bipedal Creatures , ACM Transactions on Graphics 32.6 (2013)
在强化学习和不确定环境下的行走控制取得了极好的效果。视频2013年 Flexible Muscle-Based Locomotion for Bipedal Creatures
CMA-ES 算法的基本特点有:
- 无梯度优化,不使用梯度信息,
- 局部搜索中无梯度算法通常比梯度算法慢,通常需要 倍的评估,
- 在复杂优化问题non-separable, ill-conditioned, or rugged/multi-modal 上表现良好。
1. CMA-ES 算法步骤
CMA-ES的核心想法是通过对正态分布 中协方差矩阵 的调整来处理变量之间的依赖关系和scaling。算法基本可以分成以下三步
- 采样产生新解;
- 计算目标函数值;
- 更新分布参数
ES算法设计的核心就是如何对这些参数进行调整,尤其是步长参数和协方差矩阵的调整,以达到尽可能好的搜索效果。对这些参数的调整在ES算法的收敛速率方面有非常重要的影响。CMA-ES调整参数的基本思路是,调整参数使得产生好解的概率逐渐增大(沿好的搜索方向进行搜索的概率增大)。
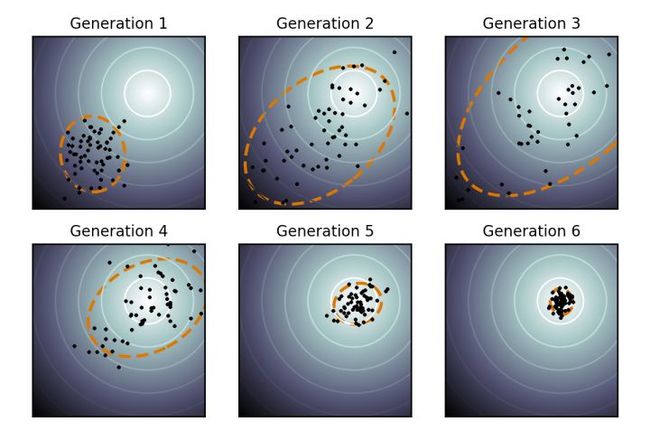
CMA-ES 的搜索过程
1. 1 采样产生新解
在CMA-ES中,每一次迭代从 中产生 个解(一般 取值为log(n)的量级)
这里的每一个 是一个搜索方向。一般的, 可以通过协方差矩阵C的特征分解 或者Cholesky 分解由标准正态分布得到,即
1. 2 计算目标函数值
对新产生的解计算对应的目标函数值 ,并对这些目标函数值排序
其中的下标表示在这些样本中排第i位。对于截断选择来说,取前 个解用于更新分布参数。还存在其他的选择方式,这里为方便使用截断选择。值的注意的是,这里的顺序只依赖于目标函数值的比较,而不依赖于目标函数值本身,即comparison based,或者说 objective value-free。
1.3 分布参数更新
使用所选择的解分别对分布参数 分别进行独立的更新。大体来说,对 的更新使用的是最大似然估计 (ML-update)
1.3.1 均值
分布的均值即为所选择的 个解的加权的最大似然估计
此式表明,均值沿着平均搜索方向移动一步.
- 这里通过组合所选择的部分解得到下一代的均值的做法称为multi-recombination, 类似于其他进化算法中的交叉(crossover operation),即不同的解之间进行交换信息multi-recombination。
- 如果权重系数取相同的 , 那么此式就是使用所选择的解的最大似然估计。在实际算法中,通常取 以强调排在最前面的那些解。
- 更新项 可以理解为对 的自然梯度信息几何优化,随机优化, 与进化策略.
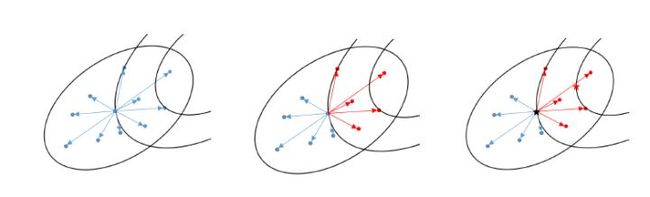
采样,选择和更新
1.3.2 进化路径/搜索路径(evolution path)
CMA-ES中,对协方差矩阵C 的更新包含rank-1 和rank- 两项,其中的rank-1 项使用的是历史搜索信息——进化路径,其构造方式为
它描述了分布均值的移动,并且将每次迭代中移动方向 做加权平均,使得这些方向中相反的方向分量相互抵消,相同的分量则进行叠加。这类似于神经网络优化中常用的Momentum。在神经网络中momentum起什么做用?因此,进化路径代表了最好的搜索方向之一。
这里面的系数因子是按照如下方式设计的:
- 因子 的设计是根据 .这是因为 ,因此可以看成是一个从上述分布采样得到的随机向量(确切的说,如果 是随机选择的)。
- 因子 的设计原理是 .这两条被称为平稳性条件(stationarity condition),使得 本身看起来像一个从当前分布 产的搜索方向 。所以 可以像一个mutation一样用来更新协方差矩阵。
- 变化率/学习率 的设计原理是 ,即学习率与所调整的变量自由度(参数个数)成反比。
1.3.3 协方差矩阵
协方差矩阵的更新的原理是
实际调整中是对此做一步迭代(一步迭代本身没有实现上式的最大化)。在此基础上,协方差的更新方式为
或者更加简洁的写成(由于前面采样中 和 的关系)
其中:
- 的更新原理是增大沿成功搜索方向的方差,即增大沿这些方向采样的概率.
- 第一项 rank-1 update 可以理解成直接把进化路径看作一个成功的搜索方向. 最初的CMA-ES只包含 rank-1 更新( ),这对小规模种群是性能优异,例如 , 以及极限情形的每一次只产生一个新解的(1+1)-CMA-ES.
- 更新的第二项的秩为 ,由于通常 所以这一项常被称为rank- update。这实际上是使用所选择的 个解的加权的最大似然估计(去除步长参数)。这一项rank update可以解释为对 的自然梯度信息几何优化,随机优化, 与进化策略,但是和前面对 的自然梯度使用的步长不同。当种群规模较大的时候 ,这项更新起着更加重要的作用。
- 学习率 的设计原理和上面一样,也就是 ,即学习率与所调整的变量自由度(参数个数)成反比。
1.3.4 步长更新
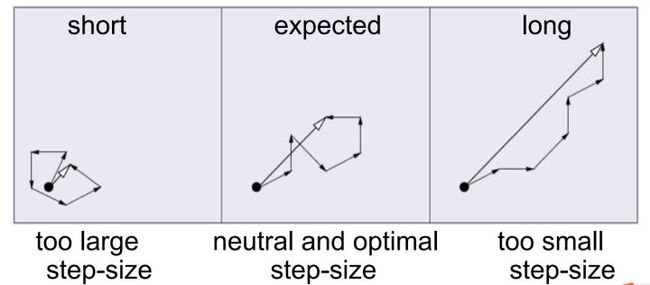
CMA-ES默认使用累积式步长调整(Cumulative step size adaptation, CSA) 。CSA是当前最成功、用的最多的步长调整方式。CSA的原理可以从方面来理解:相继搜索的方向应该是共轭的。
- 如果相继的搜索方向之间正相关(夹角小于pi/2),那么表明步长太小,应该增大;
- 如果相继搜索方向之间是负相关的,那么表明步长太大,应该减小。
进化路径
与前面的进化路径相似,构造另一个进化路径(有些文献里面称为共轭路径conjugate evolution path)
其中
- 更新项在很多论文里写成 ,其中的 。因此,这个方向实际上是去掉尺度因子D之后的搜索方向。
- 在平稳性条件下有 ,即搜索路径可以看成是一个n维标准正态分布的随机向量。因此 其模长服从卡方分布 ,并且 ,而 .因此,如果模长大于平均值,则指数上是正的,步长变大,否则指数上是负的,步长减小。这实现了前面的intuitive idea.
- 考虑另一种解释. 在上述路径中取 ,即不进行累积。这时候 实际上是“平均搜索方向”,并且“大致”服从标准正态分布。从这个角度来说,步长调整可以理解为,如果所选择的这些解的平均长度大于全体的平均长度,那么长度就增加,反之如果较好的这部分的平均长度小于全体的平均,那么长度应减小。这类似于xNES中步长调整的含义。在 情况下的累积则代表通过历史平均来消除/减小随机性。
- 是调整步长变化幅度的控制参数,通常设置为 . 此外实验上来说,算法对 的设置不敏感,可以取到 以进行快速调整,大部分情况下效果相差不大。
注:在如果每次迭代步长几乎不变,大致有 , 那么会有如下近似
即相继的搜索方向关于协方差矩阵的逆 是共轭的,而在二次函数上,这个 收敛于Hessian矩阵(相差一个标量因子)。从这个角度来说, 被称为共轭进化路径。这个是很好的性质。
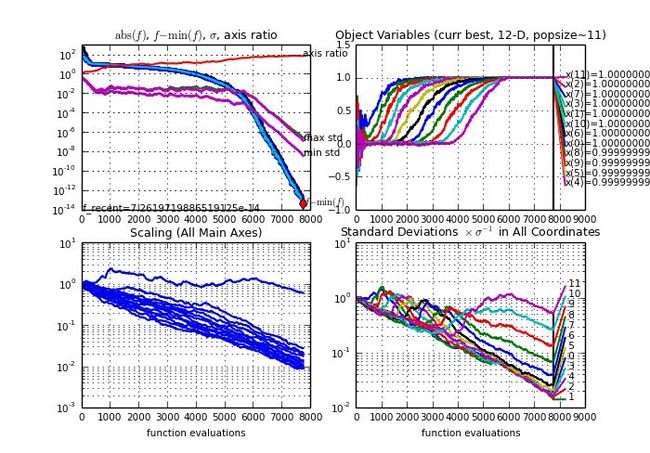
1.4 实验:A Case Study on Rosenbrock
在12-d 的Rosenbrock 函数上的一次典型运行,横轴为目标函数的评估次数(function evaluation),纵轴分别为目标函数值,各个自变量的值, 各轴向上的scaling和 . 可以看出,算法逐渐逼近最优点的过程(右上,最优点的位置在(1,...,1))就是算法逐渐学得各个轴向和轴向上的scaling的过程(左下和右下)。
2. CMA-ES的一些性质
- 在二次函数上,CMA-ES中的协方差矩阵收敛于Hessian矩阵的逆,并且收敛速率是(指数)线性的 。因此CMA-ES 是一种不使用梯度和函数值的variable-metric 方法。
- 相较于传统数学优化方法,CMA-ES 的算法行为在目标函数的单调变换下保持不变;相较于大部分进化算法,则保持了variable metric的多种不变性,其中最重要的就是在搜索空间的正交变换(旋转)下保持不变。
- 在算法中使用一个独立的步长参数是为了可以快速调整整个搜索区域的尺度。由于C的更新公式中的变化率因子都非常小(与变量个数的平方成反比),使用独立的步长因子可以在不需要对C进行精细调整的情况下快速搜索到最优点附近。
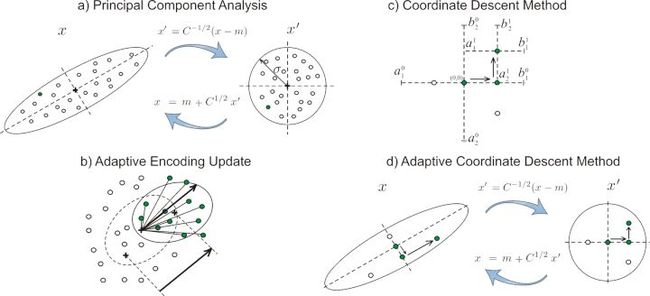
- 从变换的角度来说,实际上是用 将目标函数变成尽可能可分的(separable),并且更加接近球函数(条件数减小)。经过变换之后的函数相比原有的目标函数更加容易优化。这个过程被进一步抽象为一种自适应编码(Adaptive encoding, AE-CMA). 一个非常有意思的算法是将坐标下降法和自适应编码结合起来,得到一种自适应坐标下降 (adaptive coordinate descent).
- 很大程度上,ES算法可以看成一个局部搜索。ES中实现全局搜索的主要方式是使用Restart 策略启发式优化算法中,如何使之避免陷入局部最优解?简单来说,就是如果算法在某个位置不再改进,那么直接重新初始化换一个位置进行搜索。由于大多数多峰问题上使用较大的采样规模(即种群规模)总是有益的,因此每次初始化通常会增大采样规模(IPOP),或者交替使用较大的和较小的种群进行全局搜索和局部搜索(Bi-Pop)。
注:有些作者指出,这里的 不应该称为步长,而应该称为 scale factor 或者mutation strength,原因是有时候即使 算法仍然能很好的收敛,只要 并且更快。这里为了方便我们就称为步长了。
自适应坐标下降=坐标下降+自适应编码
3. 关于ES理论方面
ES本身是进化计算领域相对来说理论比较完善的。早年间,随机优化(包含模拟退火这类算法)常常声称的优势是全局收敛性,即在 时算法以概率一收敛到全局最优。但是在ES领域则有不同的看法。
We believe that global convergence is rather meaningless in practice. The pure random search converge with probability one to the global optimum of functions belonging to a broad class, where the main assumption is that a neighborhood of the global optimum should be reachable by the search distribution with a positive probability. However, the convergence rate is sub-linear with degree 1/n, therefore, the running time is proportional to . Even for moderate dimension, e.g., n=10, this is prohibitively slow in practice.
He (M. Powell) believed that local optimality is all one can get in the nonconvex case.
因此,ES领域的理论研究主要关注算法的收敛速率方面。ES领域通常认为,全局收敛性实际上没什么意义,我们从来不可能真的让 ,而且这往往是通过牺牲局部搜索的效率换来的. 真正重要的是给定初始化之后,能够快速地收敛到局部最优。如果这个局部最优仍然太差不可接受,那么通过restart 重新搜索。
ES领域的理论分析(大部分情况下不包含协方差调整部分)主要包含以下三个方面(方法):
- Progress rate:这个是ES领域传统的理论分析方法,H.-G. Beyer的整本书The Theory of Evolution Strategies都是基于此方法。Progress rate考虑的是算法一步迭代中对目标函数的改进幅度的期望。在只考虑步长调整的情况下,通过对维度n取极限能极大的简化问题的复杂性。目前这仍然是最重要的理论分析方法之一。
- Convergence rate:收敛速率的定义方式基本类似于经典优化里面收敛速率,除了搜索的点的序列是随机的。近年来在这个方向有较大的进展Linear Convergence of Comparison-based Step-size Adaptive Randomized Search,最主要的结论之一就是证明了这种基于比较的算法(comparison-based adaptive randomized search) 在一大类问题上能够线性收敛,并且收敛速率 ,即与变量数目成反比(这是无梯度优化的普遍特点Some Comments on Gradient-Free Optimization)。
- Runtime lower bound: 考虑的是为达到某个给定的精度所需要的迭代(function evaluation)的次数。由于不对维度取极限,能够对较低维度的问题给出更加准确的bound,如 -ES在1/5法则的步长调整下runtime bound为 。这方面的很多文章发在Theoretical Computer Science上。
除此之外,随着对自然梯度和ES的关系认识的逐步加深,近年来有一些从自然梯度流(正态分布流形上的微分方程)的角度来分析算法在极限情形下的收敛性质。这方面主要的结论有,在二次函数上
即梯度流方程是线性收敛的,并且收敛速率 。这个速率远大于前面提到的以及实际观察到的 ,目前没有很好的解释. 这方面更多内容和资料可参考信息几何优化,随机优化, 与进化策略
注:ES的理论研究主要集中于步长调整方面,大部分情况下不涉及协方差矩阵的调整。这主要是由于协方差矩阵的变量参数太多,难以控制。另一方面,从变换的角度来说,协方差矩阵的调整(或者协方差矩阵的平方根矩阵)将一个不可分的椭圆等高面 (f-value sub-level set)映射成一个球函数的等高面,然后在这个球函数上使用步长调整方式。而在球函数上,自适应调整的步长是线性收敛的。所以从这个角度来说,研究球函数上步长调整方式的收敛速率具有重要性。
4. CMA-ES 的一些改进
在前面的算法步骤中,每一次迭代产生新解都需要进行矩阵分解。矩阵分解的复杂度与变量个数的三次方成正比,这使得算法每次迭代需要耗费的计算非常多。实际算法中通过隔一些迭代次数才进行一次分解以降低计算复杂度(能这么做的原因在于C的学习率都很小,变动缓慢)。同时注意到,在采样中实际使用的并不是协方差矩阵本身,而是它的“平方根”,即满足 的矩阵A。因此,一种更高效的方案是不直接更新和分解协方差矩阵,而是直接迭代更新矩阵A,从而将复杂度降到二次方。这就是Cholesky CMA-ES。值的注意的是,这里并不一定要求A是上三角的。使用上三角矩阵的更新方式写起来更加复杂,不便于向量化编程,但在采样过程中的矩阵-向量乘法计算会少一半。
上面指出协方差矩阵的更新中,rank- 部分可以解释成自然梯度。那么更直接的,如果考虑以平方根A为参数的正态分布,使用自然梯度下降就得到自然进化策略(natural evolution strategies, NES). 这一思路下,一个更加有效、避免估计Fisher矩阵的方案是使用局部坐标系和指数映射的exponential NES。
为进一步降低算法的内部复杂度,近年来有一些工作使用特殊形式的协方差矩阵,避免使用稠密矩阵造成的计算量。后面我们会单独介绍这部分工作。
步长调整方式CSA具有极好的数学性质和性能,但是仍然有一些缺点。其一,CSA强烈依赖于标准正态分布,如果基础不是标准的正态分布,CSA可能就会不成立,算法性能会严重下降。其次,如果采样规模(即种群规模)很大,CSA的性能会变差。近年来,开始有一些将传统的1/5法则推广到population的情形的方法,并且性能很好。不过目前这些方法普遍还缺少理论分析。
注:1/5法则是早期基于对(1+1)-ES最大改进的理论分析提出的一种步长调整方式,直观来说就是要使目标函数的改进幅度(progress)最大,那么步长的设计应该使得产生一个由于当前解的概率大约是1/5左右。具体来说:In order to obtain nearly optimal (local) performance of the (1 + 1)-ES with isotropic mutation in real-valued search spaces, tune the mutation strength σ in such a way that the (estimated) success rate is about 1/5.
5. 程序
下面列举一些CMA-ES的程序:
- 一个python的库pypi-cma,是N. Hansen本人更新维护的,安装和使用特别简单.
- CMA-ES 源代码的主页CMA-ES Source Code,包含各种语言写的程序,尤其是多种C++的实现(包含并行libcmaes)和Matlab的版本CMA-ES Matlab。
- Shark Machine Learning Library,这个包含着上面的网页中,单独拿出来说是因为这是一个广泛的包含多种机器学习和进化计算方面的C++库。这个库在Windows上安装略有不便,在Linux上一次编译完成感觉太好了。
Wiki 主页上有一个非常简短的Matlab 程序CMA-ES - Wikipedia,只有最基本的算法实现,可以用于了解算法。如果使用的话,应该尽可能使用上面的完整的Code,包含了多种变体,对约束、噪声的处理,以及restart 策略处理复杂优化问题。
部分参考文献
[1] The CMA Evolution Strategy: A Tutorial
[2] Adaptive Coordinate Descent
[3] The Theory of Evolution Strategies
[4] Theory of Evolution Strategies: a New Perspective
[5] Linear Convergence of Comparison-based Step-size Adaptive Randomized Search
[6] Convergence Analysis of Evolutionary Algorithms That Are Based on the Paradigm of Information Geometry
[7] Impacts of invariance in search: When CMA-ES and PSO face ill-conditioned and non-separable problems