【算法】大话数据结构学习笔记
【算法】大话数据结构学习笔记
- 前言
- 三、线性表
- 四、栈和队列
- 五、串
- KMP模式匹配算法
- 六、树
- 二叉树的遍历
- 线索二叉树
- 树、森林与二叉树的转换
- 赫夫曼树和赫夫曼编码
- 七、图
- 图的存储结构
- 图的遍历
- 深度优先遍历(Depth-First-Search)DFS
- 广度优先遍历(Breadth-First-Search)BFS
- 最小生成树
- 普里姆算法(Prim)
- 克鲁斯卡尔算法(Kruskal)
- 最短路径
- 迪杰斯特拉算法
前言
数据结构是学习编程的必要基础之一,不把这个搞定将来真的很难有大的发展。。很多招聘企业在应聘要求中都写有熟悉数据结构与算法,去研究一种更好的新算法不是我能做到的,把前人研究过并且已经得到验证和实际使用的算法学会就好,如果能运用到自己的工作学习中就更好了。
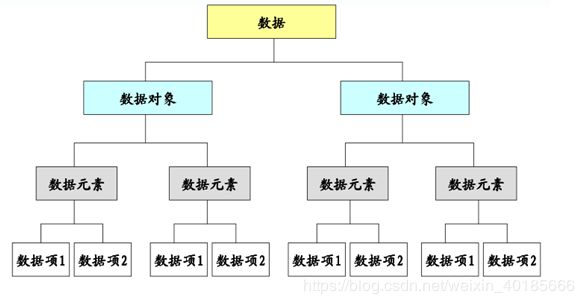
这本书的特点是比较俏皮,像是聊天讲故事,但是刚开始的基本属于实在是绕人。数据、数据元素、数据项、数据对象、数据结构这些看着就头疼。http://www.cnblogs.com/zhanggaofeng/p/5672610.html 这篇博客讲的很清楚。
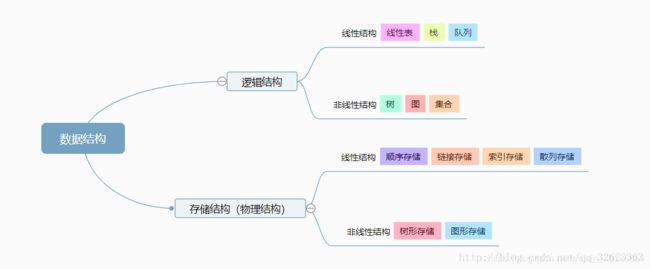
关于逻辑结构和物理结构的区别,下图取自 https://blog.csdn.net/qq_32623363/article/details/79198037 我觉得可能书里将的会比较合理一些,逻辑结构涉及到的是数据的内容,逻辑结构是由数据的内容决定的;而物理结构是单纯的数据在内存中存储的结构,和数据本身的内容关系不大。
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作
算法具有五个基本特性: 输入、输出、有穷性、确定性和可行性。
算法设计的要求:正确性、可读性、健壮性、时间效率高和存储量低
计算算法的时间复杂度其实是一个很基础的东西,目前看主要就是先看执行次数和问题规模的函数f(n),然后推导大O阶的方法计算出时间复杂度,其实只需要关注f(n)中的最高阶的阶数,因为在问题规模趋向于无限大的时候,起决定性作用的就是这个最高阶。计算方法如下:

三、线性表
定义:0个或多个数据元素的有限序列。
线性表的顺序存储结构最典型的就是数组,可想而知,在知道元素的位置时,读写元素是非常快的,但是对于插入和删除就会很麻烦,所以它比骄适合数据数目变化不大但是要经常读取的情况;
链式存储结构是采用的p->data p->next这样的结构进行数据的存储的,容易忽略的一点是,对于在链表中插入和删除数据本身操作随便比较简单但是找到这个元素还是要从头开始查找;
静态链表是一个比较新颖的方式,是在数组中实现类似于链表的机制,要点就是头元素和尾元素留出来保存链表的头元素以及空链表的头元素;
双向链表其实就是相比单向链表多了一个前驱指针;这里面比较重要的一点是**”循环链表“**也就是将链表尾部的元素的next指针改为头元素实现一个循环链表;
四、栈和队列
定义:限制了只能在表头和表尾进行操作的线性表。
-
顺序存储的栈
本质上就是一个数组
例子:对于栈空间为5的栈,空栈和满栈的情况如下:里面比较重要的和汇编里讲的一样,主要是看栈顶指针,时刻指向栈顶元素,所以当空栈时,栈顶指针指向的是-1;

两栈共享空间适用于此消彼长的情况,一个大的数组头和尾分别作为两个栈的栈底; -
链式存储的栈——链栈
比较关键的点在于,链栈的栈顶就是单链表的表头。一般单链表会有一个头结点,它保存着链表的一些基本参数,而它的next指针指向链表的第一个节点,如果链表为空则头结点的next指针指向null;而链栈中,头结点其实就是我的栈,如下图:可以看到,LinkStack本质上就是头结点,它保存着栈中元素数目,而top指针指向链表的第一个元素也就是栈顶元素。因此栈为空也就意味着top=null;

下面是链栈的出栈操作,其中值得注意的是对栈空的检验,二是释放栈顶元素的时候,申明一个新的指针指向栈顶元素然后释放该指针就可以释放对应的空间;

-
顺序队列
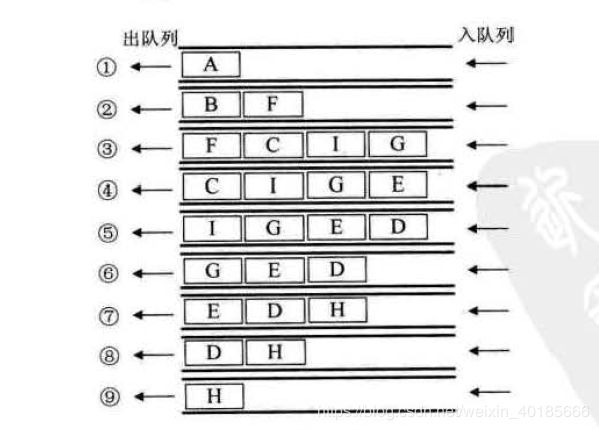
有点类似于接收帧数据解包的环形缓冲池,它的原理就是循环顺序队列; -
链队列
本质上就是一个只能在头部删除节点和尾部插入节点的单链表。保留链表的头结点,里面可以保存队列数目,next指针指向队列的第一个元素,实际上链队列的结构体只包含两个结点指针,front指向头结点,它不是第一个元素!rear指向最后一个指针,需要注意的地方就是,当队列中只剩下一个元素而且要将其出队列时,需要将rear指向修改为和front相同,不然的话rear的指向就是错误的了。可以在每次出队的时候加一个判断,看这个要出对的节点是不是rear指向的节点,是的话就要修改rear和front相同。

五、串
比较有趣的一个记忆字符串大小的方法,就是假想成一本字典,越往后越大。字符串的处理不同的语言基本上是相似的,查找、合并、子串等等。
KMP模式匹配算法
对于朴素的模式匹配算法,将子串的首字符与大串的字符进行逐个比较,整个比较过程文字描述比较困难,还好比较容易想到它的实现过程。KMP的思想就是先去考察子串的结构,先分析出子串中各个位置字符的相似程度再根据此进行相应的处理。算法就是针对一个字符串生成一个next数组:

该书中提供的KMP计算next数组的函数中,数组和字符串的索引竟然是从1开始的。对代码进行了测试发现的确是不行。下图中采用的例子是书上提供的。正确的next结果应当是012345678.很明显就错在索引上,因此需要对这个代码进行修改。将sublime配置成C++编译器很简单,之前的博客中也有写:【工具】Subline配置为C++编译器

六、树
只有一个根节点,它的所有子树互不相交。树有很多属性和性质,比如深度、度、双亲、孩子之类的,一般看一遍就能理解。关于二叉树以及完全二叉树,它们有更多的特殊属性,我觉得知道就可以,有些可能会在实际应用中用到。接下来是关于树的存储结构:
首先,完全二叉树适合顺序存储,这个是比较好理解的。而对于一般的二叉树,显然使用链式结构更合适。

二叉树的遍历
方法比较绕人,我总结的规律是:
- 前序遍历:任意一个结点,先遍历自己,再遍历左子树,最后遍历右子树。这里比较重要的是,节点的任意性,也就是说,当从根节点出发的时候,先取根节点、再取根节点的左子树,到了左子树,下一步应当是左子树的左子树而不是根节点的右子树;
- 中序遍历:任意一个结点,先遍历左子树,再遍历自己,最后遍历右子树。这里同样和上面一样,重要的地方在于对于左子树,它也可能会有左子树。这里会有一个嵌套的过程;
- 后序遍历:任意一个结点,先遍历左子树,再遍历右子树,最后遍历自己。和上面的都一样,嵌套决定了根节点是最后一个被遍历的;
理解了上面的内容后,其实很容易想到遍历二叉树的算法应当怎么写。首先,从上面的分析可以看到,其实根节点的左子节点其实是左子树的根节点,这就意味着需要再对这个节点进行一次左子节点的遍历。因此会用到递归调用:
二叉树的数据结构如下:
typedef struct BitNode //这是一个二叉树中的节点
{
datatype data; //存放节点中实际的数据
struct BitNode *lchild,*rchild; //左右孩子节点
}BitNode,*BitTree; //创建一个结构体指针只需要使用BitTree即可
//前序遍历:可以看出,是先对某个节点遍历,然后遍历它的左子节点,而后是右子节点
void PreOrderTraversing(BitTree T)
{
if(T==null)
return; //递归是需要截止条件的,如果这个元素不存在就返回
//DoSomething with T->data 涉及到遍历的具体目的因为这里已经能直接取到节点的数据了,这一段操作结束意味着完成了对该点的遍历
PreOrderTraversing(T->lchild); //lchild本身也是结构体指针类型,所以就是BitTree类型
PreOrderTraversing(T->rchild);
}
//中序遍历:可以看出,是先对某个节点的左子节点遍历,然后遍历它自己,而后是右子节点
void PreOrderTraversing(BitTree T)
{
if(T==null)
return; //递归是需要截止条件的,如果这个元素不存在就返回
PreOrderTraversing(T->lchild); //lchild本身也是结构体指针类型,所以就是BitTree类型
//DoSomething with T->data 涉及到遍历的具体目的因为这里已经能直接取到节点的数据了,这一段操作结束意味着完成了对该点的遍历
PreOrderTraversing(T->rchild);
}
//后序遍历:可以看出,是先对某个节点的左子节点遍历,然后遍历它的右子节点,而后是它自己
void PreOrderTraversing(BitTree T)
{
if(T==null)
return; //递归是需要截止条件的,如果这个元素不存在就返回
PreOrderTraversing(T->lchild); //lchild本身也是结构体指针类型,所以就是BitTree类型
PreOrderTraversing(T->rchild);
//DoSomething with T->data 涉及到遍历的具体目的因为这里已经能直接取到节点的数据了,这一段操作结束意味着完成了对该点的遍历
}
之前我看过两遍这个程序都没有理解的很完善,这一次应该是比较透彻,上述代码是自己独立想出来的,其实最不好理解的就是关于递归的目的。其实遇到的每一个节点和根节点的操作是一样的。所谓的前中后序本质上的区别是对于一个节点以及它的左右孩子的遍历先后顺序。
线索二叉树
源头是因为有一种二叉树叫做:扩展二叉树

原本这个#是为了根据某个次序例如前序输入时能够在内存中创建这个结构的二叉树,后来发现这个#不用浪费,那么就可以它们来存放某个次序下各个点的前驱后继。这样相当于建立了一个双向链表,此外,左右孩子到底是前驱后继还是真的左右孩子,则个需要一个标志量来识别。

线索二叉树的数据结构如下:

和普通二叉树最主要的区别就是有左右两个标志量。
树、森林与二叉树的转换
森林就是若干个树,而这些树的根节点可以看作是兄弟,那么就仍然可以把森林转换成一个二叉树。
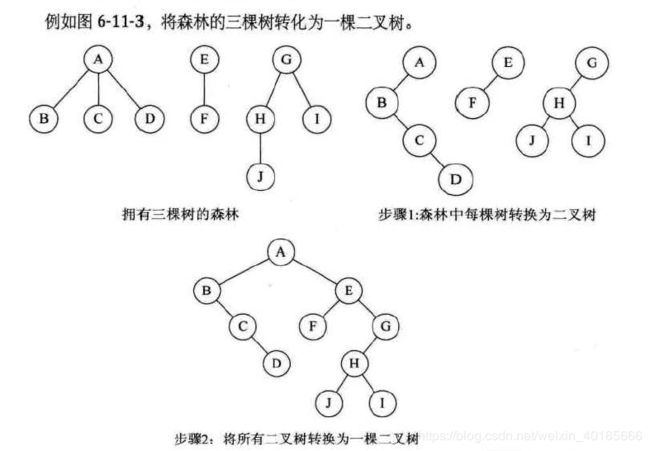
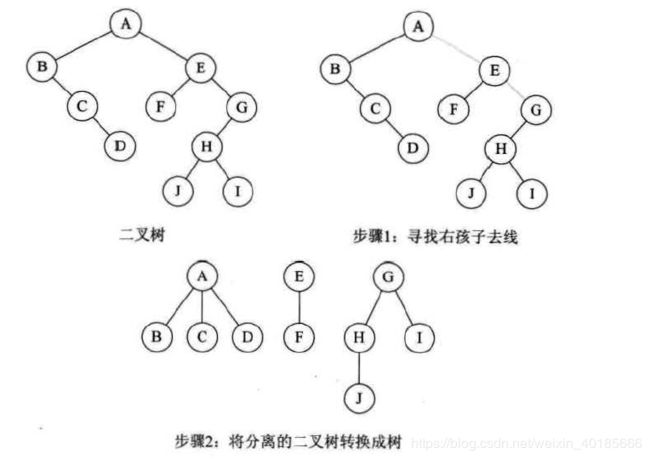
二叉树转换成树:

加线的目标是任意一个节点的左孩子的所有右孩子,去线是删除除根节点外所有节点和右孩子的连线。
二叉树转森林:很明显,如果根节点有右孩子那就直接打断,所有的右孩子都是不同树的根节点。
赫夫曼树和赫夫曼编码
这一块书上讲的很浅,我在去年曾经听师兄讲过类似的思想。出现最频繁的字符的编码替换成占用空间最小的编码,而不经常出现的则使用相对长的编码。
七、图
图中的顶点vertex一定是非空的,但边edge是可以为空的。其他定义很多比较繁杂,建议直接看书回忆。比如邻接、度、出度入度、简单路径简单环。接下来是关于连通图的相关知识:无向连通图是指图中任意两个顶点之间都存在路径即连通的。下面是关于连通分量的概念,注意这只是无向图,有向图中则对应着强连通分量。

生成树其实就是保持顶点数目不变,但是减少边到n-1条。

关于图的基本定义和术语如下:

图的存储结构

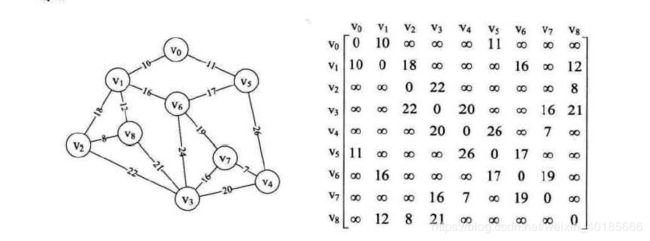
这个设计中,顶点组成的数组可以方便的实现顶点的查找,而知道了顶点的索引后也能够很方便的在邻接矩阵即一个二维数组中找到对应的信息。很容易想象无向图的邻接矩阵是一个对称阵,而有向图则不是。并且还可以将权重放入邻接矩阵中实现对它的保存。因此这个结构目前看来是非常适合实现计算机对图的存储的。

但是如果边数相对顶点数少很多的话,邻接矩阵实际上很浪费内存,因此需要实现一种更适合的结构,邻接表。和邻接矩阵不同的地方就是,邻接矩阵换成了链表。
无向图:
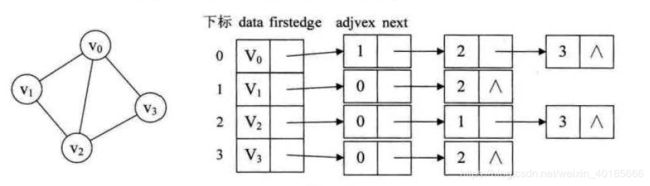
有相同有:

显然,邻接表对于有向图来说很不友好,因为现在可以很轻松的查到出度,但入度就得对整个图进行遍历,因此最好的方式就是同时存有出度和入度。这种类型叫做十字链表,好处就是任意一个顶点可以很方便的解决出度和入度的问题。
邻接表对于无向图来说也存在一定的弊端,如下:‘

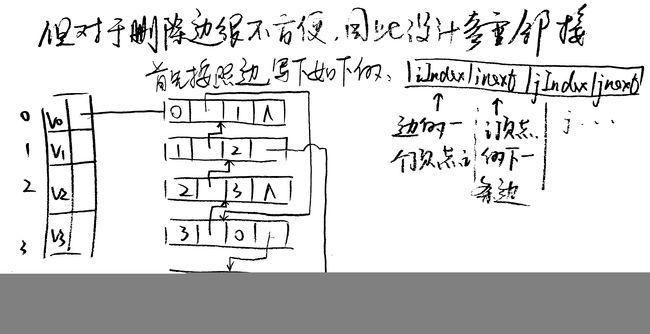
图的遍历
深度优先遍历(Depth-First-Search)DFS
遇到岔路就挑最右边的走,当这个方法走到最深的地方发现最后的那个岔路口所有的出口点都已经走过了,就回退上一点,去走右数第二个出口,如此往复,最终就可以找到所有的点。这里面是一个递归的过程,怎么看出来的?任意取一个点,对与其邻接的还未遍历过的点依次进行遍历,但在遍历完与其邻接的第一个点的时候,又会对与这个点邻接的点进行遍历,如此递归下去,直到在遍历某一个点时,发现所有与其邻接的点都已经被遍历过了,这时就可以返回上一层遍历剩下的邻接点最终完成全部遍历。
接下来是对采用了邻接矩阵的无向图进行深度优先遍历的算法:
//邻接矩阵的数据结构
typedef chacr VertexType;
typedef int EdgeType;
#define MAXVEX 100
#define INFINITY 65535
typedef struct
{
VertexType vexs[MAXVEX]; //顶点存放数组
EdgeType arc[MAXVEX] [MAXVEX);//邻接矩阵的二维数组
int numVertexes, numEdges ; //现有顶点数和边数
}MGraph;
bool visited[MAXVEX]; //遍历标志量
//邻接矩阵深度优先递归算法
void DFS(MGraph G,int i) //MGraph是图的结构体,i是0~VNum-1间任意一个数字,代表任意一个点
{
int j;
//对G.vexs[i]进行操作
visited[i]=1; //该顶点已遍历到
for(j=0;j<G.numVertexes;j++) //遍历邻接表的第i行
if(G.arc[i][j]==1&&!visited[j]) //只要这个点是i点的邻接点并且没有被遍历过
DFS(G,J);
}
//需要注意的是!!!!!!!!!!!!!!!!!
//上面的代码是针对连通图的,也就是说如果图不是连通图,那么存在DFS执行完后还有没有遍历到的。因此需要再进行一次封装:
void DFSTraversing(MGraph G)
{
for(int i=0;i<G.numVertexes;i++)
visited[i]=false;
for(int i=0;i<G.numVertexes;i++)
if(!visited[i]) //如果说是一个连通图,第一次i=0时,就已经所有的点都遍历了,for循环后面的都不会通过
DFS(G,i);
}
以上是邻接矩阵的使用方法,邻接表基本一样,主要就是循环条件变成了判断指针是否为空。

广度优先遍历(Breadth-First-Search)BFS

如上图可以看出,广度优先有点类似于是树的层序遍历,在图上任意找一个点,然后根据与它的邻接关系分层。这个思想还是比较好接受和记忆的。实现的方法是使用一个辅助队列,对于上面这个例子,如果采用邻接矩阵的形式进行存储,处理过程如下:
- 首先遍历一下索引i=0的顶点,并且将索引号入队列;
- 如果队列不为空,出队列提取到索引号,此时出队列的索引号顶点已经被遍历过了;
- 搜索所有顶点找出与i顶点邻接的所有顶点,对其进行遍历并将其索引号入队列;
- 返回步骤2
//邻接矩阵的数据结构
typedef chacr VertexType;
typedef int EdgeType;
#define MAXVEX 100
#define INFINITY 65535
typedef struct
{
VertexType vexs[MAXVEX]; //顶点存放数组
EdgeType arc[MAXVEX] [MAXVEX);//邻接矩阵的二维数组
int numVertexes, numEdges ; //现有顶点数和边数
}MGraph;
bool visited[MAXVEX]; //遍历标志量
Queue Q;
//邻接矩阵广度优先递归算法
void BFS(MGraph G) //MGraph是图的结构体,i是0~VNum-1间任意一个数字,代表任意一个点
{
//初始化队列
for(int i=0;i<G.numVertexes;i++) //防止图不是联通图
{
if(!visited[i]) //防止不是连通图
{
//对该索引号的顶点进行遍历
visited[i]=true; //这个是一个连通图中的第一个点,对于一个连通图这个代码只执行一次
Enqueue(Q,i);
while(!IsQueueEmpty(Q)) //这里的循环实现的是对整个连通图的层序遍历
{
Dequeue(Q,&i);
for(int j=0;j<G.numVertexes;j++)
{
if(G.arc[i][j]==1&&!visited[j]) //找到所有与其邻接的顶点,完成遍历并且入队列
{
//遍历j顶点
visited[j]=1;
Enqueue(Q,j);
}
}
}
}
}
}
上面的代码的注释已经很清楚了,对于广度优先遍历的理解也比上一次看更加深刻,看来代码还是得自己写,看再多效果也不如写的好。邻接表的原理差不多,就不详细写了。
最小生成树
对于类似于书中提到的,村庄之间架设电信网线的例子,这是一个网的问题,因为顶点之间的连线出现了距离这一权值,所以就要研究一个成本最低的方案,即权值之和最小。这里比较简单,因为很容易联想到一个概念:**生成树,就是保证图中n个顶点只有n-1个边连接起来。**而所有生成树中代价最小的就是最小生成树。有两种算法可以实现:
普里姆算法(Prim)
克鲁斯卡尔算法(Kruskal)
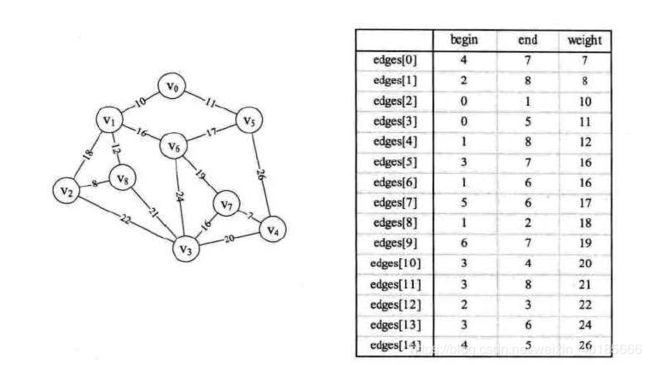
关于回路检测我觉得书讲的很差,完全没理解是什么原因能够实现对回路的检查,仅仅是照着代码讲,就像高中的时候英语试卷的讲解,照着这是对的讲,某一部莫名其妙的就得到了答案正确的结论。