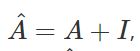GCN pytorch实现 笔记

欢迎移步我的个人博客
https://tkipf.github.io/graph-convolutional-networks/

GCN Part1：定义

卷积，因为过滤器参数通常在图中的所有位置共享

输入：

• 每个节点i的特征描述xi：为一个N×D的特征矩阵X (N:节点数，D:输入特征数)
• 图以矩阵的典型形式输入：通常以邻接矩阵A(或其某个函数)的形式出现

输出：

• 节点级别的输出：一个N*F的矩阵Z，N是节点数目，F是每个节点的特征数目
• 图级别的输出：通过引入某种形式的池化来建模。

每个神经网络层都可以写成非线性函数


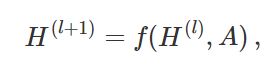
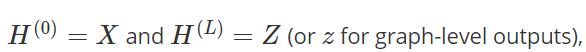
L是层数，具体的模型的不同只有f()函数如何选择并且参数化的 。

GCN Part2：一个简单例子

是神经网络第l层的权重矩阵
是非线性激活函数
该模型的两个局限性：

1. 与A相乘意味着，对于每个节点，我们对所有相邻节点的所有特征向量求和，但不包括节点本身(除非图中存在自循环)。我们可以通过在图中执行自循环来“修复”这个问题:我们只需将单位矩阵添加到A中。
2. A通常不是归一化的，因此与A的乘法会完全改变特征向量的比例(我们可以通过观察A的特征值来理解这一点)。使A归一化，如行的和为1。D^-1A避免了这个问题，D是对角节点度矩阵。与D ^- 1^A相乘相当于取相邻节点特征的平均值。

结合这两点，我们得到了新的传播公式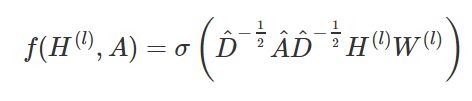

I是单位矩阵。

D_hat是A_hat的对角节点度矩阵

GCN Part3：嵌入Zachary’s karate club

Karate club图，颜色表示通过基于模块化的聚类得到的群落

我们采用一个随机初始化权重的三层GCN。在训练之前，我们只需将图的邻接矩阵和X=I插入到模型中(即单位矩阵，因为我们没有任何节点特征)。
这个3层的GCN在前向传播期间执行三个传播步骤，且对每个节点的3阶邻域进行卷积(所有节点到3“跳”远)。

该模型生成了这些节点的嵌入，与图的群组结构非常相似，如下图。此时，我们还没有进行任何的训练更新。
然后有一个新的方法

GCN Part4：半监督学习

由于我们的模型中的所有内容都是可微分和参数化的，所以我们可以添加一些标签，训练模型并观察嵌入的反应。我们可以使用Kipf & Welling (ICLR 2017)中引入的GCNs半监督学习算法。我们只是为每个类/社区标记一个节点(在下面的视频中突出显示的节点)，并开始进行一些迭代训练。
效果视频在这里
注意，该模型直接产生了一个二维的潜在空间，我们可以立即可视化。我们观察到，3层的GCN模型能够线性地分离社区，每个类只给出一个标记的示例。假设模型没有输入节点的特征描述，这是一个不错的结果。同时，初始的节点特征是可以提供的，这正是我们在论文(Kipf & Welling, ICLR 2017)中描述的实验中所做的，以实现对大量图数据集的最新分类结果。