人工智能6.1 -- 机器学习算法篇（一）数据清洗、回归（含实践）
人工智能
- python，大数据，机器学习，深度学习，计算机视觉
-
六、机器学习算法篇（一）数据清洗、回归（含实践） - 前言
- 目录
- 算法热身
- 结论：
- 附：
- 注：
- 拓展：
- 理论知识 ---- 纯干货
- 线性回归公式推导：
- ==梯度下降算法（重点）==
- 实践
- 例1. 广告花费 与 销售额 的关系
- 例2. 预测商品销售量 ----- Lasso回归
- 例3. 回归比较
- 例4. ROC曲线
python，大数据，机器学习，深度学习，计算机视觉
六、机器学习算法篇（一）数据清洗、回归（含实践）
前言
前面博文机器学习导论篇说过，
如果结果y值连续 ------ 回归
如果结果y值离散 ------ 分类
附：
X ---------> f ----------> Y
自变量 函数 因变量 -----（初中）
定义域 映射 值域 -----（高中）
特征 模型 结果 -----（机器学习）
目录
-
线性回归
- 高斯分布
- 最大似然估计MI
- 最小二乘法的本质
-
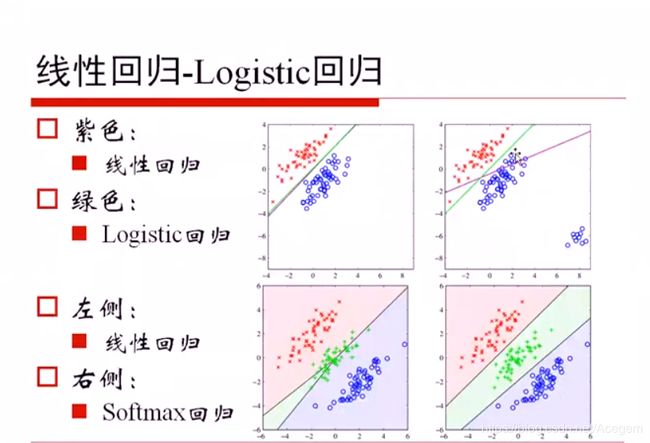
Logistic回归
- 分类问题的首选算法
-
多分类：Softmax回归
- 目标函数
-
技术点
- 梯度下降算法
- 最大似然估计
- 特征选择
算法热身
判断是否是素数，几种算法的性能比较
import numpy as np
from time import time
import math
def is_prime(x):
return 0 not in [x%i for i in range(2, int(math.sqrt(x))+1)]
def is_prime3(x):
flag = True
for p in p_list2:
if math.sqrt(x) <p:
break
if x%p == 0:
flag = False
break
if flag:
p_list2.append(x)
return x # 使用filter() 必须return
#test 求素数 算法性能比较
if __name__ == "__main__":
a = 2
b = 100000
#方法1：直接计算
t_start = time()
p = [p for p in range(a, b) if 0 not in [p%d for d in range(2, int(math.sqrt(p))+1)]] # 千万别忘了+1
print(time()-t_start)
print(p)
#方法2：利用filter
t_start = time()
#重点：python3新规定，用filter处理后的是一个object，要想打印需要先转化成list。python2不用转list
p = list(filter(is_prime, range(a, b)))
print(time()-t_start)
print(p)
#方法3：利用filter和lambda
t_start = time()
is_prime2 = (lambda x: 0 not in [x%i for i in range(2, int(math.sqrt(x))+1)])
p = list(filter(is_prime2, range(a, b)))# filter筛选
print(time()-t_start)
print(p)
#方法4：定义 ----- 此法代码看着稍微多点但实际效率很高
t_start = time()
p_list = []
for i in range(2, b): # 遍历i判断i是否是素数，i = 2,3,...
flag = True
for p in p_list: # p是已判定为素数
# 下面“代码主体部分”的前提条件
if math.sqrt(i) < p:
break
# “代码主体部分”
if i%p == 0:
flag = False
break
if flag:
p_list.append(i)# p_list = 2,...
print(time()-t_start)
print(p_list)
#方法5：定义和filter
t_start = time()
p_list2 = []
p_list2 = list(filter(is_prime3, range(2, b)))
print(time()-t_start)
print(p_list2)
# 求概率小游戏
# print('----------------------------')
# a = 1180
# b = 1230
# p_list2 = []
# p = np.array(filter(is_prime3, range(2, b+1)))
# p = p[p >= a]
# print(p)
# p_rate = float(len(p)) / float(b-a+1)
# print('从',a,'到',b,'素数的个数：',len(p),'\t','素数的概率：', p_rate)
# print('从', a, '到', b, '合数的个数：', b-a+1-len(p), '\t', '合数的概率：', 1-p_rate)
运行结果：
C:\Python\Anaconda3\python.exe C:/AI/AnacondaProject/1_numpy.py
1.8530809879302979
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, （省略）
1.9677658081054688
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, （省略）
2.1472527980804443
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, （省略）
0.44384026527404785
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, （省略）
0.37399816513061523
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, （省略）
结论：
可以看出 使用filter()会提高效率，但用lambda效率几乎没变，效率最高的是方法5，其核心思想是方法4，方法5是在方法4的基础上加了filter()。
附：
关于python3中filter的使用，引用菜鸟教程的实例，如下：
注：
- python的filter筛选，即查找。filter(函数fun, 列表list) # 将list的元素一个一个的放到函数fun里执行。用函数fun来筛选list。
- 相当于php中的回调函数：
- 查找 array_filter()：array_filter($arr, “fun”)
- 插入 array_walk()：array_walk($arr, “fun”)
- 替换 array_map()：array_map(“fun”, $arr)
拓展：
其实求素数最高效的是埃氏筛法 ----- Eratosthenes埃拉托色尼筛选法，下面代码了解下：
def _int_iter():#生成器生成从3开始的无限奇数序列
n = 1
while True:
n = n + 2
yield n
def _not_divisible(n):#定义筛选函数
return lambda x:x % n > 0
def primes():
yield 2 #先返回一个2
it = _int_iter() # 初始序列
while True:
n = next(it) # 返回序列的第一个数
yield n
it = filter(_not_divisible(n), it) # 构造新序列
for n in primes():#构造循环条件，使之可以输出任何范围的素数序列
if n < 1000:
print(n)
else:
break
理论知识 ---- 纯干货
AUC越接近1越好，如果算出AUC值接近0.5则相当于白算了（还不如随机选呢）。（AUC后续再说，不容易解释）
线性回归公式推导：
两个变量：y = ax + b
多个变量：
h θ ( x ) h_\theta~(x) hθ (x) = θ 0 \theta_0 θ0 + θ 1 x 1 \theta_1x_1 θ1x1 + θ 2 x 2 \theta_2x_2 θ2x2 + … + θ n x n \theta_nx_n θnxn 。
记 θ \theta θ = [ θ 1 \theta_1 θ1, θ 2 \theta_2 θ2, …, θ n \theta_n θn]，特征x = 对角阵，如下：
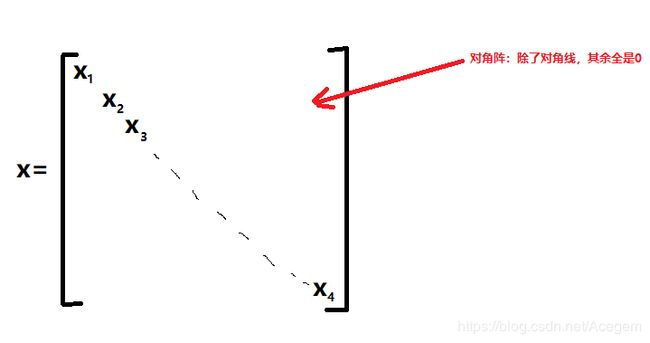
则：
h θ ( x ) h_\theta~(x) hθ (x) = θ T \theta^T θTx， 再加上误差，进一步地：
由于误差服从高斯分布，故误差的概率：
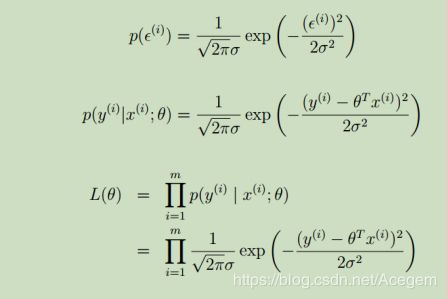
梯度下降算法（重点）
特征选择：1次方，2次方，3次方，选哪个好呢，次数高或许能全拟合上，但有可能造成过拟合，并不是说次数越高越好。
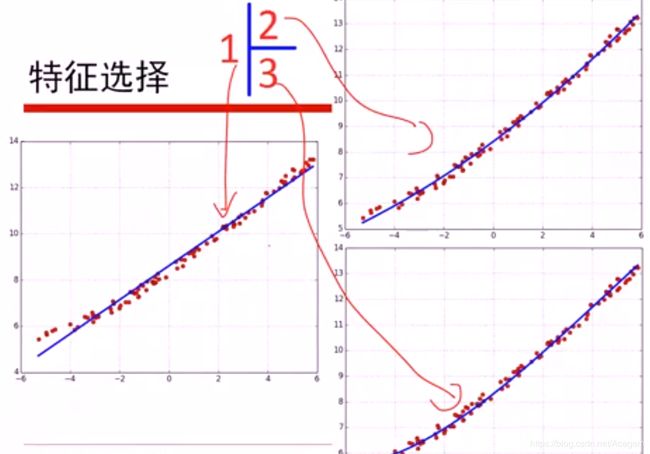
上面：R2只是一个记号，R2有可能为负值。
sigmoid函数：g(x) = 1/(1+e-x)，如下，可推出其导数 g’(x) = g(x)*(1-g(x))。
Logistic回归：g( θ \theta θTx) = 1/(1 + exp(- θ \theta θTx))
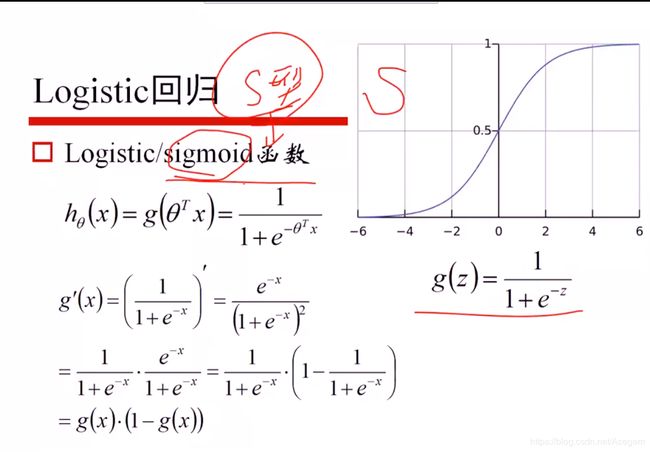附：高数知识
注：将上面函数上移0.5个单位即得到sigmoid函数。
可以反着推，假设发生的概率P和不发生的概率1-P的比值再取对数，是线性的。由此可推出概率P恰好是sigmoid函数。如下：
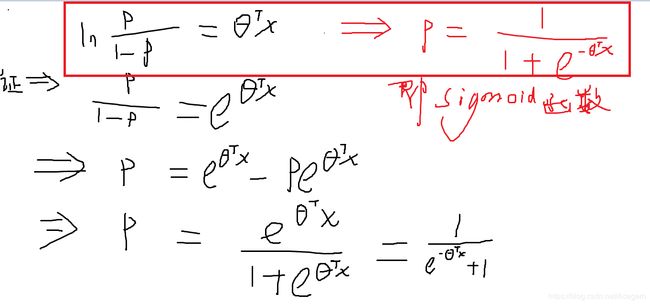
混淆矩阵：
俗话说：“随机过程随机过，混淆矩阵易混淆。”
下面，我通过一个简单的例子说明白上面概念。不负此博文
举例：是否生病？
-
（1）
实际：正 ---- 生病
预测：P是 ---- 生病
预测结果：T ---- 预测的正确
记为：TP -
（2）
实际：正 ---- 生病
预测：N否 ------ 未生病
预测结果：F ---- 预测的错误
记为：TN -
（3）
实际：负 ---- 未生病
预测：P是 ----- 生病
预测结果：F ----- 预测错了 -
（4）
实际：负 ----- 未生病
预测：N否 ----- 未生病
预测结果：T ----- 预测正确
注：P是又称为阳性，N否又称为阴性 ------ 来自于医学。 -
TPR=TP Rate：
实际生病的情况，诊断成生病的概率。— 诊断对
TPR越高越好，最好接近于1。
应用：实际生病了要求我们必须给诊断出来。 -
FPR= FR Rate：
实际没生病，诊断成生病的概率。 ----- 误诊
FPR越低越好，最好接近于0
应用：实际没生病要求我们必须不能误诊。
所以TPR和FPR这两个很重要！
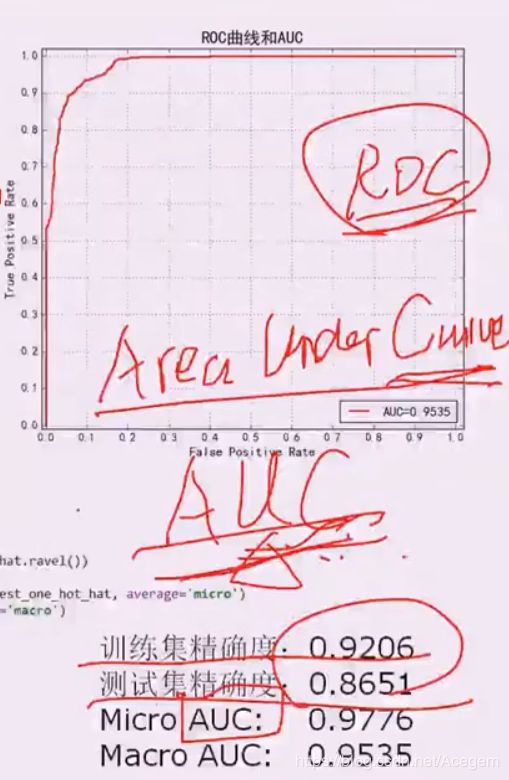
ROC曲线 和 AUC面积（Area Under Curve）：
ROC曲线下的面积，即AUC(Area Under ROC Curve)：AUC反映的是分类器对样本的分类排序能力。AUC越大，分类器模型对样本分类的效果就越好（见下面小图）。AUC是衡量学习器优劣的一种性能指标。
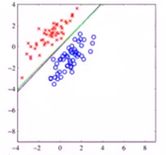
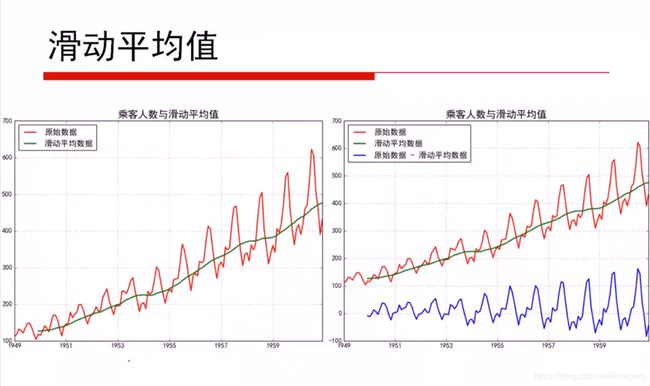
AUC面积范围应该在[0.5, 1]之间才有价值，越接近于1说明模型越的好。
- 若AUC = 1，则是完美分类器。
- 若低于0.5则没价值（模型没有预测价值）：因为若诊断预测正确的概率低于0.5这个模型就没价值了，比如我来诊断是否生病 我不用模型随机猜像抛硬币一样还有0.5的概率蒙对呢。
实践
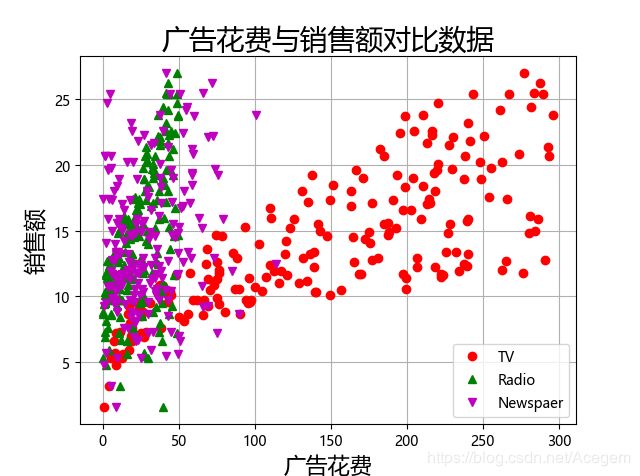
例1. 广告花费 与 销售额 的关系
#!/usr/bin/python
# -*- coding:utf-8 -*-
import csv
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from pprint import pprint
if __name__ == "__main__":
path = 'Advertising.csv'
# # 手写读取数据
# f = file(path)
# x = []
# y = []
# for i, d in enumerate(f):
# if i == 0:
# continue
# d = d.strip()
# if not d:
# continue
# d = map(float, d.split(','))
# x.append(d[1:-1])
# y.append(d[-1])
# pprint(x)
# pprint(y)
# x = np.array(x)
# y = np.array(y)
# Python自带库
# f = file(path, 'r')
# print f
# d = csv.reader(f)
# for line in d:
# print line
# f.close()
# # numpy读入
# p = np.loadtxt(path, delimiter=',', skiprows=1)
# print p
# print '\n\n===============\n\n'
# pandas读入
data = pd.read_csv(path) # TV、Radio、Newspaper、Sales
# x = data[['TV', 'Radio', 'Newspaper']]
x = data[['TV', 'Radio']]
y = data['Sales']
print(x)
print(y)
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
# 绘制1
plt.figure(facecolor='w')
plt.plot(data['TV'], y, 'ro', label='TV')
plt.plot(data['Radio'], y, 'g^', label='Radio')
plt.plot(data['Newspaper'], y, 'mv', label='Newspaer')
plt.legend(loc='lower right')
plt.xlabel(u'广告花费', fontsize=16)
plt.ylabel(u'销售额', fontsize=16)
plt.title(u'广告花费与销售额对比数据', fontsize=20)
plt.grid()
plt.show()
# 绘制2
plt.figure(facecolor='w', figsize=(9, 10))
plt.subplot(311)
plt.plot(data['TV'], y, 'ro')
plt.title('TV')
plt.grid()
plt.subplot(312)
plt.plot(data['Radio'], y, 'g^')
plt.title('Radio')
plt.grid()
plt.subplot(313)
plt.plot(data['Newspaper'], y, 'b*')
plt.title('Newspaper')
plt.grid()
plt.tight_layout()
plt.show()
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, random_state=1)
print(type(x_test))
print(x_train.shape, y_train.shape)
linreg = LinearRegression()
model = linreg.fit(x_train, y_train)
print(model)
print(linreg.coef_, linreg.intercept_)
order = y_test.argsort(axis=0)
y_test = y_test.values[order]
x_test = x_test.values[order, :]
y_hat = linreg.predict(x_test)
mse = np.average((y_hat - np.array(y_test)) ** 2) # Mean Squared Error
rmse = np.sqrt(mse) # Root Mean Squared Error
print('MSE = ', mse,)
print('RMSE = ', rmse)
print('R2 = ', linreg.score(x_train, y_train))
print('R2 = ', linreg.score(x_test, y_test))
plt.figure(facecolor='w')
t = np.arange(len(x_test))
plt.plot(t, y_test, 'r-', linewidth=2, label=u'真实数据')
plt.plot(t, y_hat, 'g-', linewidth=2, label=u'预测数据')
plt.legend(loc='upper right')
plt.title(u'线性回归预测销量', fontsize=18)
plt.grid(b=True)
plt.show()
运行结果：
C:\Python\Anaconda3\python.exe C:/AI/AnacondaProject/8.regression/8.1.Advertising.py
TV Radio
0 230.1 37.8
1 44.5 39.3
2 17.2 45.9
3 151.5 41.3
4 180.8 10.8
.. ... ...
195 38.2 3.7
196 94.2 4.9
197 177.0 9.3
198 283.6 42.0
199 232.1 8.6
[200 rows x 2 columns]
0 22.1
1 10.4
2 9.3
3 18.5
4 12.9
...
195 7.6
196 9.7
197 12.8
198 25.5
199 13.4
Name: Sales, Length: 200, dtype: float64
上面是线性回归预测的商品销售量，下面用Lasso回归来预测
例2. 预测商品销售量 ----- Lasso回归
文件8.2.LinearRegression_CV.py
完整代码如下：
# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
# sklearn 著名的机器学习包
from sklearn.model_selection import train_test_split # train_test_split函数把数据分成：训练数据、测试数据
from sklearn.linear_model import Lasso, Ridge # Lasso , Ridge回归
from sklearn.model_selection import GridSearchCV # GridSearch按照网格方式一个个搜，CV交叉验证 = Cross Verification
if __name__ == "__main__":
# pandas 读入
data = pd.read_csv('Advertising.csv') # TV、Radio、Newspaper、Sales
x = data[['TV', 'Radio', 'Newspaper']] # 将读取的DataFrame格式的data数据的TV列、Radio列、Newspaper列拿出来
# x = data[['TV', 'Radio']]
y = data['Sales']
print(x)
print(y)
"""
train_test_split()生成训练数据，测试数据。 ----- 来自开头的sklearn包
参数：
random_state=1 表每次取的训练数据是相同的，测试数据也是相同的。这句话也可以不加
train_size=0.75 表75%的当训练数据，剩下的25%当测试数据。也可用固定值， train_size=100（100个当训练数据，剩余的当测试数据）
或者也可用test_size=0.25 表25%当测试数据
"""
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1) # 默认train_size=0.75 默认random_state=0
# 生成Lasso模型
model = Lasso()
# model = Ridge()
# 用来Lasso建模的参数alpha
alpha_can = np.logspace(-3, 2, 10) # 从 10^(-3)（即0.001）~ 10^2（即100），取10个数
# print('科学计数法 alpha_can =', alpha_can)
np.set_printoptions(suppress=True) # 使用小数四舍五入形式，不用科学计数法。
print('alpha_can =', alpha_can)
# 建模：Lasso模型，参数为alpha_can的5折的交叉验证
lasso_model = GridSearchCV(model, param_grid={'alpha': alpha_can}, cv=5)
# 把训练数据fit喂进去，以便看上面的生成的10个alpha哪一个是最优的！
lasso_model.fit(x_train, y_train)
# 训练后可得到：最优的alpha参数
print('超参数：\n', lasso_model.best_params_)
# 线图美观，保证y值递增。（可以去掉这三句话看看结果，去掉不算错）
order = y_test.argsort(axis=0) # 对y值从小到大排序，记录改变了哪些位置order。
y_test = y_test.values[order] # 按照这些order对y值进行排序
x_test = x_test.values[order, :] # 按照这些order也对x值排序（因为x，y值是一一对应的）
# test：用测试数据测试建的模型怎样
y_hat = lasso_model.predict(x_test) # y_hat预测值
# 得到测试分数，即R^2， R^2 = 1-RSS/TSS（参考博文理论部分的知识）
print(lasso_model.score(x_test, y_test)) # 对于线性回归来说，分数score（即R^2）既使达到0.8或0.9其实也不算是非常好！
# 均方误差：y_hat是预测值（数组），y_test是实际值（数组）。预测值减实际值后的平方，再求平均值。
mse = np.average((y_hat - np.array(y_test))**2) # Mean Squared Erro
rmse = np.sqrt(mse)
print(mse, rmse)
t = np.arange(len(x_test)) # 测试数据的个数
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(facecolor='w')
# 红色线表真实数据
plt.plot(t, y_test, 'r-', linewidth=2, label=u'真实数据') #相当于plot(x, y)
# 绿色线表测试数据
plt.plot(t, y_hat, 'g-', linewidth=2, label=u'预测数据')
plt.title(u'线性回归预测销量', fontsize=18)
plt.legend(loc='upper right')
plt.grid()
plt.show()
运行结果：
C:\Python\Anaconda3\python.exe C:/AI/AnacondaProject/8.regression/8.2.linearRegression_CV.py
TV Radio Newspaper
0 230.1 37.8 69.2
1 44.5 39.3 45.1
2 17.2 45.9 69.3
3 151.5 41.3 58.5
4 180.8 10.8 58.4
.. ... ... ...
195 38.2 3.7 13.8
196 94.2 4.9 8.1
197 177.0 9.3 6.4
198 283.6 42.0 66.2
199 232.1 8.6 8.7
[200 rows x 3 columns]
0 22.1
1 10.4
2 9.3
3 18.5
4 12.9
...
195 7.6
196 9.7
197 12.8
198 25.5
199 13.4
Name: Sales, Length: 200, dtype: float64
alpha_can = [ 0.001 0.00359381 0.0129155 0.04641589 0.16681005
0.59948425 2.15443469 7.74263683 27.82559402 100. ]
超参数：
{'alpha': 0.5994842503189409}
0.9147734784738105
1.992871866305969 1.4116911370076561
例3. 回归比较
文件8.3.ElasticNet.py
完整代码如下：
import numpy as np
# 从sklearn库中的linear_model线性模型包，导入函数：线性回归, Ridge回归，Lasso回归，Elastic回归
from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV, ElasticNetCV # linear a.线性的
from sklearn.preprocessing import PolynomialFeatures # 预处理 多项式特征
# 加上管道Pipeline，以便预处理有先后顺序：先处理PolynomialFeatures再处理LinerRegression
from sklearn.pipeline import Pipeline
from sklearn.exceptions import ConvergenceWarning # 运行代码时不报汇聚类型的警告提示的。如：输入的数据太小，模型训练的太少等。见下面调用。
import matplotlib.pyplot as plt
import matplotlib as mpl
import warnings
def xss(y, y_hat):
y = y.ravel()
y_hat = y_hat.ravel()
# Version 1
tss = ((y - np.average(y)) ** 2).sum()
rss = ((y_hat - y) ** 2).sum()
ess = ((y_hat - np.average(y)) ** 2).sum()
r2 = 1 - rss / tss
# print 'RSS:', rss, '\t ESS:', ess
# print 'TSS:', tss, 'RSS + ESS = ', rss + ess
tss_list.append(tss)
rss_list.append(rss)
ess_list.append(ess)
ess_rss_list.append(rss + ess)
# Version 2
# tss = np.var(y)
# rss = np.average((y_hat - y) ** 2)
# r2 = 1 - rss / tss
corr_coef = np.corrcoef(y, y_hat)[0, 1]
return r2, corr_coef
if __name__ == "__main__":
# 忽略代码运行时的警告info
warnings.filterwarnings("ignore", category=FutureWarning, module="sklearn") # 忽略FutureWarning类型的警报
# 运行代码时不报汇聚类型的警告提示。如：输入的数据太小，模型训练的太少等。
warnings.filterwarnings(action='ignore', category=ConvergenceWarning) # 这句话同代码开头的ConvergenceWarning包的那句，都无关紧要。
np.random.seed(0) # 给定随机数的种子不变。
np.set_printoptions(linewidth=1000) # 打印时改变这一行线条宽度，为了输出结果显示都在一行，不换行，输出结果时好看
# 获取10个随机点x,y坐标
N = 9
# 制造数据x，加上噪声 ---- np.random.randn(9)
x = np.linspace(0, 6, N) + np.random.randn(N) # np.linspace(0, 6, 9) 结果：[0. 0.75 1.5 2.25 3. 3.75 4.5 5.25 6. ]
# x进行排序
x = np.sort(x)
# 制造数据y，也加上噪声
y = x**2 - 4*x - 3 + np.random.randn(N)
# 定义成列向量。一个x是一个样本，一个y也是一个样本。故设计成列向量
x.shape = -1, 1
y.shape = -1, 1
# 重点：建模。模型采用线性回归，且是多项式的形式。
models = [Pipeline([
('poly', PolynomialFeatures()), # 开头导入的预处理，多项式特征
('linear', LinearRegression(fit_intercept=False))]), # 建立LinearRegression线性回归模型，fit_intercept=False忽略截距项
Pipeline([
('poly', PolynomialFeatures()),
('linear', RidgeCV(alphas=np.logspace(-3, 2, 50), fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', LassoCV(alphas=np.logspace(-3, 2, 50), fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', ElasticNetCV(alphas=np.logspace(-3, 2, 50), l1_ratio=[.1, .5, .7, .9, .95, .99, 1],
fit_intercept=False))])
]
# 设置字体属性
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
np.set_printoptions(suppress=True)
# matplotlib显示：
plt.figure(figsize=(18, 12), facecolor='w')
# N个点，最多只需N-1阶就能100%拟合，把阶数留下来画图用。
d_pool = np.arange(1, N, 1) # 阶
m = d_pool.size
# 为每一阶的团分配不同的颜色，画图用
clrs = [] # 颜色
# for c in np.linspace(16711680, 255, m):
for c in np.linspace(11119999, 255, m, dtype=int): # 一定要int型，否则报错！！！
clrs.append('#%06x' % c)
line_width = np.linspace(5, 2, m)
titles = u'线性回归', u'Ridge回归', u'LASSO回归', u'ElasticNet回归' # u表utf-8
tss_list = []
rss_list = []
ess_list = []
ess_rss_list = []
# 循环遍历生成4个子图，用来画出4种回归图
for t in range(4):
model = models[t]
plt.subplot(2, 2, t+1) # 循环一次生成一个子图，共4个
# 画这9个点
plt.plot(x, y, 'ro', ms=10, zorder=N)
# 对没一阶画出它的预测值曲线
for i, d in enumerate(d_pool):
model.set_params(poly__degree=d)
model.fit(x, y.ravel()) # fit喂进去
# 获取多项式的系数并输出
lin = model.get_params('linear')['linear']
output = u'%s：%d阶，系数为：' % (titles[t], d)
if hasattr(lin, 'alpha_'):
idx = output.find(u'系数')
output = output[:idx] + (u'alpha=%.6f，' % lin.alpha_) + output[idx:]
if hasattr(lin, 'l1_ratio_'): # 根据交叉验证结果，从输入l1_ratio(list)中选择的最优l1_ratio_(float)
idx = output.find(u'系数')
output = output[:idx] + (u'l1_ratio=%.6f，' % lin.l1_ratio_) + output[idx:]
print(output, lin.coef_.ravel())
# 把x坐标分成100份，分别得到其预测值，并相连绘制成曲线
x_hat = np.linspace(x.min(), x.max(), num=100)
x_hat.shape = -1, 1
# 模型的预测值
y_hat = model.predict(x_hat)
# 模型的准确度：score分数，即R^2
s = model.score(x, y)
r2, corr_coef = xss(y, model.predict(x))
# print 'R2和相关系数：', r2, corr_coef
# print 'R2：', s, '\n'
z = N - 1 if (d == 2) else 0
label = u'%d阶，$R^2$=%.3f' % (d, s)
if hasattr(lin, 'l1_ratio_'):
label += u'，L1 ratio=%.2f' % lin.l1_ratio_
# 画出子图
plt.plot(x_hat, y_hat, color=clrs[i], lw=line_width[i], alpha=0.75, label=label, zorder=z)
plt.legend(loc='upper left')
plt.grid(True)
plt.title(titles[t], fontsize=18)
plt.xlabel('X', fontsize=15)
plt.ylabel('Y', fontsize=15)
plt.suptitle(u'多项式曲线拟合比较', fontsize=22)
# 调整留白。参数pad: 绘图区边缘与画布边缘的距离大小， w_pad: 绘图区之间的水平距离的大小，H_pad: 绘图区之间的垂直距离的大小
plt.tight_layout(pad=5, h_pad=4)
# 调整子图间距
# plt.subplots_adjust(wspace=0.3, hspace=0.5) # 需要的时候可以调整一下子图间距！
plt.show()
# 显示另一张图：
y_max = max(max(tss_list), max(ess_rss_list)) * 1.05
plt.figure(figsize=(9, 7), facecolor='w')
t = np.arange(len(tss_list))
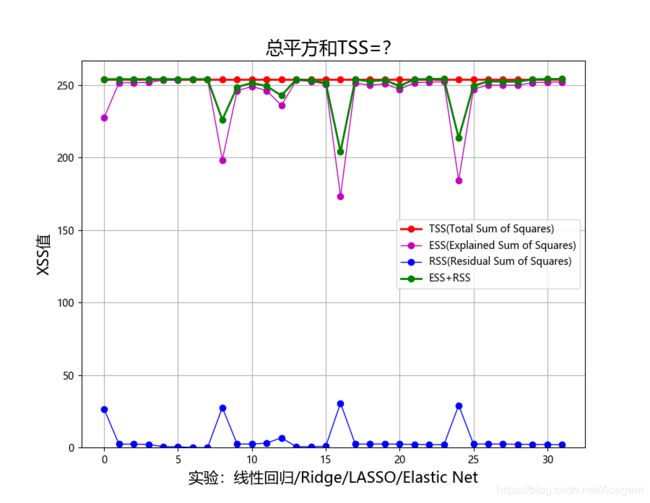
plt.plot(t, tss_list, 'ro-', lw=2, label=u'TSS(Total Sum of Squares)')
plt.plot(t, ess_list, 'mo-', lw=1, label=u'ESS(Explained Sum of Squares)')
plt.plot(t, rss_list, 'bo-', lw=1, label=u'RSS(Residual Sum of Squares)')
plt.plot(t, ess_rss_list, 'go-', lw=2, label=u'ESS+RSS')
plt.ylim((0, y_max))
plt.legend(loc='center right')
plt.xlabel(u'实验：线性回归/Ridge/LASSO/Elastic Net', fontsize=15)
plt.ylabel(u'XSS值', fontsize=15)
plt.title(u'总平方和TSS=？', fontsize=18)
plt.grid(True)
plt.show()
运行结果：
C:\Python\Anaconda3\python.exe C:/AI/AnacondaProject/regression/8.3.ElasticNet.py
线性回归：1阶，系数为： [-12.12113792 3.05477422]
线性回归：2阶，系数为： [-3.23812184 -3.36390661 0.90493645]
线性回归：3阶，系数为： [-3.90207326 -2.61163034 0.66422328 0.02290431]
线性回归：4阶，系数为： [-8.20599769 4.20778207 -2.85304163 0.73902338 -0.05008557]
线性回归：5阶，系数为： [ 21.59733285 -54.12232017 38.43116219 -12.68651476 1.98134176 -0.11572371]
线性回归：6阶，系数为： [ 14.73304785 -37.87317494 23.67462342 -6.07037979 0.42536833 0.06803132 -0.00859246]
线性回归：7阶，系数为： [ 314.30344622 -827.89446924 857.33293186 -465.46543638 144.21883851 -25.67294678 2.44658612 -0.09675941]
线性回归：8阶，系数为： [-1189.50149198 3643.69109456 -4647.92941149 3217.22814712 -1325.87384337 334.32869072 -50.57119119 4.21251817 -0.148521 ]
Ridge回归：1阶，alpha=0.109854，系数为： [-11.21592213 2.85121516]
Ridge回归：2阶，alpha=0.138950，系数为： [-2.90423989 -3.49931368 0.91803171]
Ridge回归：3阶，alpha=0.068665，系数为： [-3.47165245 -2.85078293 0.69245987 0.02314415]
Ridge回归：4阶，alpha=0.222300，系数为： [-2.84560266 -1.99887417 -0.40628792 0.33863868 -0.02674442]
Ridge回归：5阶，alpha=1.151395，系数为： [-1.68160373 -1.52726943 -0.8382036 0.2329258 0.03934251 -0.00663323]
Ridge回归：6阶，alpha=0.001000，系数为： [ 0.53724068 -6.00552086 -3.75961826 5.64559118 -2.21569695 0.36872911 -0.0222134 ]
Ridge回归：7阶，alpha=0.033932，系数为： [-2.38021238 -2.26383055 -1.47715232 0.00763115 1.12242917 -0.52769633 0.09199202 -0.00560197]
Ridge回归：8阶，alpha=0.138950，系数为： [-2.19287493 -1.9189901 -1.21620537 -0.19324078 0.49303633 0.05458084 -0.09693178 0.02114898 -0.00140213]
LASSO回归：1阶，alpha=0.222300，系数为： [-10.41556797 2.66199326]
LASSO回归：2阶，alpha=0.001000，系数为： [-3.29932625 -3.31989869 0.89878903]
LASSO回归：3阶，alpha=0.013257，系数为： [-4.83524033 -1.48721929 0.29726322 0.05804667]
LASSO回归：4阶，alpha=0.002560，系数为： [-5.08513199 -1.41147772 0.3380565 0.0440427 0.00099807]
LASSO回归：5阶，alpha=0.042919，系数为： [-4.11853758 -1.8643949 0.2618319 0.07954732 0.00257481 -0.00069093]
LASSO回归：6阶，alpha=0.001000，系数为： [-4.53546398 -1.70335188 0.29896515 0.05237738 0.00489432 0.00007551 -0.00010944]
LASSO回归：7阶，alpha=0.001000，系数为： [-4.51456835 -1.58477275 0.23483228 0.04900369 0.00593868 0.00044879 -0.00002625 -0.00002132]
LASSO回归：8阶，alpha=0.001000，系数为： [-4.62623251 -1.37717809 0.17183854 0.04307765 0.00629505 0.00069171 0.0000355 -0.00000875 -0.00000386]
ElasticNet回归：1阶，alpha=0.021210，l1_ratio=0.100000，系数为： [-10.74762959 2.74580662]
ElasticNet回归：2阶，alpha=0.013257，l1_ratio=0.100000，系数为： [-2.95099269 -3.48472703 0.91705013]
ElasticNet回归：3阶，alpha=0.013257，l1_ratio=1.000000，系数为： [-4.83524033 -1.48721929 0.29726322 0.05804667]
ElasticNet回归：4阶，alpha=0.010481，l1_ratio=0.950000，系数为： [-4.8799192 -1.5317438 0.3452403 0.04825571 0.00049763]
ElasticNet回归：5阶，alpha=0.004095，l1_ratio=0.100000，系数为： [-4.07916291 -2.18606287 0.44650232 0.05102669 0.00239164 -0.00048279]
ElasticNet回归：6阶，alpha=0.001000，l1_ratio=1.000000，系数为： [-4.53546398 -1.70335188 0.29896515 0.05237738 0.00489432 0.00007551 -0.00010944]
ElasticNet回归：7阶，alpha=0.001000，l1_ratio=1.000000，系数为： [-4.51456835 -1.58477275 0.23483228 0.04900369 0.00593868 0.00044879 -0.00002625 -0.00002132]
ElasticNet回归：8阶，alpha=0.001000，l1_ratio=0.500000，系数为： [-4.53761647 -1.45230301 0.18829714 0.0427561 0.00619739 0.00068209 0.00003506 -0.00000869 -0.00000384]
例4. ROC曲线
# -*-coding:utf-8-*-
import numbers
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.svm import SVC
from sklearn.preprocessing import label_binarize
from numpy import interp
from sklearn import metrics
from itertools import cycle
import warnings
if __name__ == '__main__':
# 忽略代码运行时的警告info
warnings.filterwarnings("ignore", category=FutureWarning, module="sklearn") # 忽略FutureWarning类型的警报
np.random.seed(0)
pd.set_option('display.width', 300)
np.set_printoptions(suppress=True)
n = 300
x = np.random.randn(n, 50)
y = np.array([0]*100+[1]*100+[2]*100)
n_class = 3
alpha = np.logspace(-3, 3, 7)
clf = LogisticRegression(penalty='l2', C=1)
clf.fit(x, y)
y_score = clf.decision_function(x)
y = label_binarize(y, classes=np.arange(n_class))
colors = cycle('gbc')
fpr = dict()
tpr = dict()
auc = np.empty(n_class+2)
mpl.rcParams['font.sans-serif'] = u'SimHei'
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(7, 6), facecolor='w')
for i, color in zip(np.arange(n_class), colors):
fpr[i], tpr[i], thresholds = metrics.roc_curve(y[:, i], y_score[:, i])
auc[i] = metrics.auc(fpr[i], tpr[i])
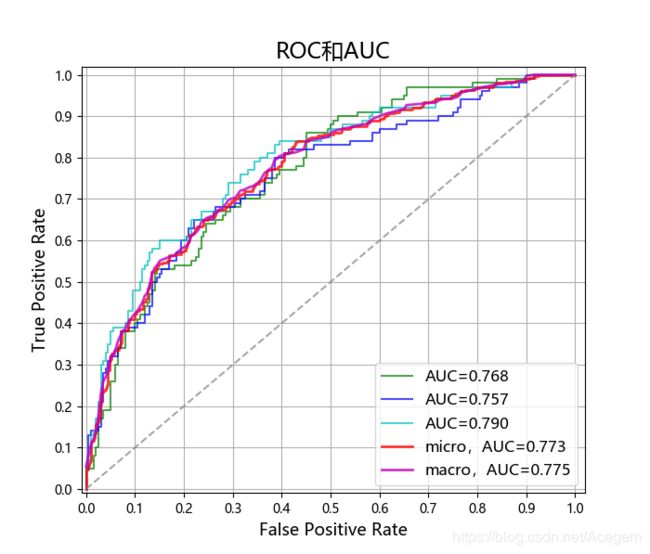
plt.plot(fpr[i], tpr[i], c=color, lw=1.5, alpha=0.7, label=u'AUC=%.3f' % auc[i])
# micro
fpr['micro'], tpr['micro'], thresholds = metrics.roc_curve(y.ravel(), y_score.ravel())
auc[n_class] = metrics.auc(fpr['micro'], tpr['micro'])
plt.plot(fpr['micro'], tpr['micro'], c='r', lw=2, ls='-', alpha=0.8, label=u'micro，AUC=%.3f' % auc[n_class])
# macro
fpr['macro'] = np.unique(np.concatenate([fpr[i] for i in np.arange(n_class)]))
tpr_ = np.zeros_like(fpr['macro'])
for i in np.arange(n_class):
tpr_ += interp(fpr['macro'], fpr[i], tpr[i])
tpr_ /= n_class
tpr['macro'] = tpr_
auc[n_class+1] = metrics.auc(fpr['macro'], tpr['macro'])
print(auc)
print('Macro AUC:', metrics.roc_auc_score(y, y_score, average='macro'))
plt.plot(fpr['macro'], tpr['macro'], c='m', lw=2, alpha=0.8, label=u'macro，AUC=%.3f' % auc[n_class+1])
plt.plot((0, 1), (0, 1), c='#808080', lw=1.5, ls='--', alpha=0.7)
plt.xlim((-0.01, 1.02))
plt.ylim((-0.01, 1.02))
plt.xticks(np.arange(0, 1.1, 0.1))
plt.yticks(np.arange(0, 1.1, 0.1))
plt.xlabel('False Positive Rate', fontsize=13)
plt.ylabel('True Positive Rate', fontsize=13)
plt.grid(b=True)
plt.legend(loc='lower right', fancybox=True, framealpha=0.8, fontsize=12)
# plt.legend(loc='lower right', fancybox=True, framealpha=0.8, edgecolor='#303030', fontsize=12)
plt.title(u'ROC和AUC', fontsize=17)
plt.show()
运行结果：
