二维傅里叶变换的理解和使用
目录
- 似模似样的前言
- 一维傅里叶
- 二维傅里叶
似模似样的前言
最近的瑕疵检测项目需要在有纹理的产品上做很细致的检测。由于当前做项目使用的还是halcon居多,目前知道的方法还是傅里叶变换比较靠谱。
但仅靠halcon自带的样例并不能很好的理解和使用傅里叶,决定综合网上其他同学的理解,写下这篇博客,从原理到工程应用都解析一下。
一维傅里叶
我们先从一维傅里叶开始说起,一维傅里叶主要是对原信号做时域到频域的转换,大体意思就是各种连续信号可以被分解为不同的正弦和余弦信号。
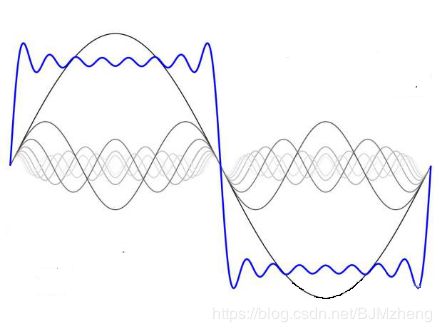
类似于上图中的蓝色信号,可分解为n多的正余弦信号,这种理解同学们在脑中过一下就好,反正傅里叶同学就这么觉得。当然这个还算在时域上的演示,其实能从原信号转换到如此结果,还可以有另一种很直观的显示。
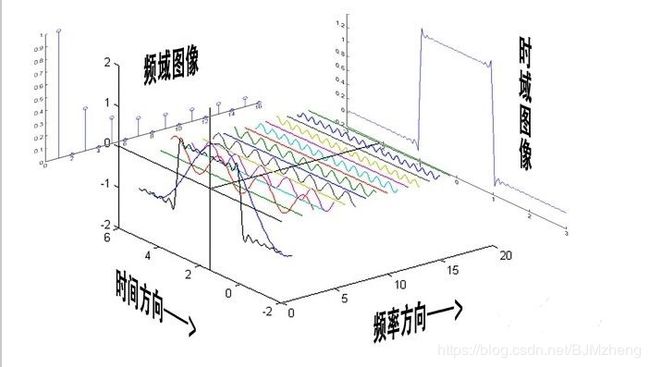
通过本复制粘贴小王子的时空忍术,窃取到上面的图片,同学们可以在上图中看到两幅图像,时域图像和频域图像。时域图像很直观,就是那些七彩斑斓的正余弦相加得到的最终图像,而频域图像就是各分量的表示,横坐标表示频率,纵坐标为幅值。
我一向把编程理解为施法,那请各位大魔法师想象一下,你对着一个莫名其妙的连续信号大声施咒“Fourier Tran… Tran… Tran… TransForm”,然后它就瞬间爆炸,成为那些彩色正余弦,之后你就可以在时间方向和频率方向观测到两幅图像了。
更细致的解释有很多,有很多大神做了更详细的解释,但本文到此为止。
然后现在的问题是怎么进行两者的转换?根据我查阅的资料,可以理解为计算原信号与某个正弦波的***相关性***

上图是我个人使用的c#程序运行截图,其中上方为原始图像
Γ ( x ) = sin ( x ∗ 4 / 180 ∗ P I ) + sin ( x ∗ 8 / 180 ∗ P I ) + 5 \Gamma(x) = \sin(x*4/180*PI)+\sin(x*8/180*PI)+5\, Γ(x)=sin(x∗4/180∗PI)+sin(x∗8/180∗PI)+5
我把它与 sin ( x ∗ 4 / 180 ∗ P I ) \sin(x*4/180*PI)\, sin(x∗4/180∗PI)相乘,得到下图。两幅图像采样点都是90.然后把第二幅图像的所有点的y值相加,得到约45.根据公式
幅值 = Sum/(采样点数量/2)
为什么要除以2,个人理解是哪怕一样的正弦相乘,正负号也没了,那就得到了双倍的快乐,所以除一下。本人目前只是验证了这个方法,至于为什么这样?相信各位大魔法师也不难百度到。
一维傅里叶的结果中,x=0处的结果为直流分量,相当于是信号平均值的映射,其他的值相对于定义域的中间对称。(让同学们了解一下,可能会辅助应用,具体为什么,可能要待小弟后续补充了)
现在看起来一维傅里叶的理解已经万事具备了,知道大致原理,知道怎么计算频率分量,之后的使用目前来看有以下几条:
1.通过FT得到频域图,去除高频部分再IFT得到消除高频噪声干扰的信号(应用于一个不圆度检测项目,还是一个有文化的客户主动要求)
2.可以分离不同频率段的信号,分析需要的频率段(应用于某信号分析项目,但最终未成功)
从上面的应用介绍也能发现博主的工作是多么心酸。
二维傅里叶
之后就来到了今天的重点,对图像的傅里叶分析。对图像的傅里叶分析其实也好理解,就是逐行逐列的使用一维傅里叶,把每一行的灰度信息理解为函数的y值。变换后的频域图主要信息集中在图像的四角,很多时候需要进行中心化,方便使用者更直观的使用。演示图如下:

上面三张分别是原图 频域图 中心化后频域图,原图的信息会以特定规律出现在频域图上。你可以这么理解原图中某个方向存在亮度变换,他就会以该方向垂直的一个点显示在频域图上。对其进行操作就会在原图上得到相对应的变换。到这一步,各位魔法师理解了吗?如果没有,那我就勉为其难再解释一下。
图像正中间为直流分量,表示平均灰度的映射,外围为频域信号,如果原图是一个左半边为255,右半边为0 的图片,转换后就会得到一张中间有一条白色直线的图。他表示主要的频率变换都在纵向上。



是不是发现符合预期,经过手阻滤波器之后,纵向的纹理基本消失。本魔法学徒果然还是有潜力的。
二维傅里叶的意义在我的理解中是类似滤波器的存在,就是给你做频域滤波的,什么高通低通带通带阻。你只要理解了它的意义,你就能很专业的使用它。这也是我在发现应用工程师有时候应用起来反而超过我的时候自我安慰的话。555555
下面的内容可能就不再是应用层的了,本博主之后会解释一下公式。没有兴趣的同学可以退散了。


