pytorch建立神经网络模型

学会利用torch.nn.Sequential、torch.nn.Module、torch.nn.MSEloss、torch.optim各包构建神经网络

1、torch可利用已有Sequential结构直接生成网络，也可以继承Module来自定义网络
2、损失函数一般回归模型可用MSEloss（最小二乘法）,二分类模型可用BCEwithLogitsloss（二分类交叉熵）,多分类模型可用CrossEntropyLoss（交叉熵损失）【具体损失函数由另一篇博文记录】
3、优化方法的基础是梯度下降法，即参数=参数-学习率*梯度，在此基础上针对学习率及梯度方向两个因素，进行变化，衍生出六种不同的优化方法
    -SGD,如将所有样本均纳入进行梯度下降的学习中，则运算量巨大，因此该方法实行的是随机选择批量样本进行梯度下降学习
    该方法存在学习时长依旧较长，并且受方向选择的制约，容易在某些维度的极小值处停下而错失其他维度下降的方向
    -SGD+momentum，该方法将方向变化考虑其中，在计算当前梯度变化时，一部分取决于当前梯度值，一部分取决于上一步的梯度方向，二者同时形成新梯度向量
    -Nesterov Momentum，该方法也将维度方向考虑其中，只是在计算梯度变化时，先计算当前梯度值，然后在此基础上，计算当前梯度方向，二者再形成新梯度向量
    以上三种优化方法属于SGD及其改进（加Momentum）；另外一大类是Per-parameter adaptive learning rate methods（逐参数适应学习率方法），即从学习率这个参数下手，让学习率不在固定，而是在学习过程中，学习率也进行变化。
    -Adagrad 首先使用学习率而不是直接将使用梯度一步到达的原因就在于，希望慢慢学习，逐渐找到最优值，那么针对不同样本，肯定有梯度大的，有梯度小的，如果学习率不变，那么对与不同样本学到的梯度就有大小区别，不利于慢慢学习，而如果在梯度大时学习率变小，梯度小时学习率增大，那么可以保证整体学习的速度非常均匀，有利于学习效果提升，于是Adagrad方法比较直接的使用学习率乘以近似梯度倒数的方式，获得上述改变学习率的效果
    但这种方式的缺点是过于简单，很容易使得学习过早停止
    -RMSProp  针对Adagrad的缺点，RMSProp想到除了使用当前梯度倒数，还可以将上一次计算的梯度考虑进去，相当于对梯度做了一个滑动平均，从而使用滑动平均后的梯度倒数对学习率进行缩放、从而获得更好效果，延长学习时间
    -Adam 相当于PMSProp的momentum版，即计算梯度倒数时，不仅考虑移动平均之前的梯度，还将梯度动量方向计算到梯度倒数之中

由此，优化方法一般使用Adam,RMSProp【具体的优化方法由另一篇博文记录】

4、影响模型效果的因素，除了选择损失函数、优化器，还有参数初始化方式
参数肯定不能初始化全为0，不然0乘以任何样本量，都是0，神经网络各层之间不会学到梯度变化；
参数可以随机初始化为任何非零值，但如果初始化的各个参数大小相差非常大，会导致中间输出值方差非常大，而再通过激活函数时，有可能落在激活函数曲线非常平缓的部位，从而出现梯度消失，因而最好将参数大小设定在一定范围或服从一定的分布，这样使得输入和输出的方差保持一致或变化不大，从而加快收敛速度

主流初始化方式一般使用 Xavier,MSRA 、网络层数不深时在 Batch Normalization 的情况下, 使用普通的小方差的高斯分布即可，或者优先采用预训练的模型进行参数初始化.【具体初始化方法由另一篇博文记录】

import torch
N=640
D_in=1000
H=128
D_out=10

batch_size=32

import torch.utils.data
import numpy as np
X=torch.randn(N,D_in)
Y=torch.randn(N,D_out)

#批训练，把数据变成一小批一小批数据进行训练。
#DataLoader就是用来包装所使用的数据，每次抛出一批数据
torch_dataset=torch.utils.data.TensorDataset(X,Y)
loader=torch.utils.data.DataLoader(dataset=torch_dataset,batch_size=batch_size,shuffle=True)# 从数据库中每次抽出batch size个样本

#1、sequential模型
model = torch.nn.Sequential(
    torch.nn.Linear(D_in,H,bias=False),
    torch.nn.ReLU(),
    torch.nn.Linear(H,D_out,bias=False)
)

torch.nn.init.normal_(model[0].weight)
torch.nn.init.normal_(model[2].weight)

#2、自定义model，利用torch.nn.Module
class TwolayerNet(torch.nn.Module):
    def __init__(self,D_in,H,D_out):
        super(TwolayerNet,self).__init__()
        
        self.linear1 = torch.nn.Linear(D_in,H,bias=False)
        self.linear2 = torch.nn.Linear(H,D_out,bias=False)
    
    def forward(self,X):
        output_linear1 = self.linear1(X)
        output_relu = output_linear1.clamp(min=0)
        y_pred = self.linear2(output_relu)
        return y_pred
model2=TwolayerNet(D_in,H,D_out)
    #自定义网络结构如何自定义参数初始化
#方法一：
#def init_weight(layer_model):
#    if isinstance(layer_model, torch.nn.Linear):
#        layer_model.weight.data.normal_(0,0.01)
#model2.apply(init_weight)
#方法二：
def init_weight(net):
    for layer_model in net.modules():
        if isinstance(layer_model, torch.nn.Linear):
            torch.nn.init.normal_(layer_model.weight,std=1e-2)
init_weight(model2)

loss_fn = torch.nn.MSELoss(reduction='sum')
learning_rate=1e-6

SGD_optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate,momentum=0,nesterov=False)
SGD_momentum_optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate,momentum=0.8,nesterov=False)
Nesterov_optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate,momentum=0.8,nesterov=True)
AdaGrad_optimizer = torch.optim.Adagrad(model.parameters(),lr=learning_rate)
RMSprop_optimizer= torch.optim.RMSprop(model.parameters(),lr=learning_rate)
Adam_optimizer = torch.optim.Adam(model.parameters(),lr=learning_rate)

optimizers=[SGD_optimizer,SGD_momentum_optimizer,Nesterov_optimizer,AdaGrad_optimizer,RMSprop_optimizer,Adam_optimizer]
models=[model,model,model,model,model,model]
loss_dis=[[],[],[],[],[],[]]

epoch=16

import matplotlib.pyplot as plt
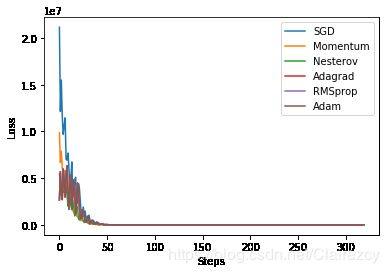
labels = ['SGD', 'Momentum','Nesterov','Adagrad', 'RMSprop', 'Adam']
for e in range(epoch):
    for i, (x,y) in enumerate(loader):
        for model_j,optimizer_j,loss_j in zip(models,optimizers,loss_dis):
            y_pred = model_j(x)
            loss = loss_fn(y_pred,y)
            optimizer_j.zero_grad()
            loss.backward()
            optimizer_j.step()
            loss_j.append(loss.data.numpy())

#print(loss_dis[0][1])
        #if i%25 == 1 and e%7==0:
            
for j in range(len(loss_dis)):                
    plt.plot(loss_dis[j], label=labels[j])
    
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.show() 

输出：