数据结构与算法Python版之北大慕课笔记(四)
数据结构与算法Python版之北大慕课笔记(四)
- 一、树
- 1. 树结构相关术语
- 2. 树的定义
- 2.1 树的定义1
- 2.2 树的定义2(递归定义)
- 二、实现树
- 1. 嵌套列表法
- 2. 节点链接法
- 三、树的应用:表达式解析
- 1. 创建表达式解析树:过程
- 2. 建立表达式解析树:规则
- 3. 建立表达式解析树:思路
- 4. 利用表达式解析树求值:思路
- 四、树的遍历Tree Traversals
- 五、优先队列Priority Queue
- 1. 用非嵌套列表实现二叉堆
- 2. 堆次序Heap Order
- 3. 二叉堆操作的实现
- 六、二叉查找树Binary Search Tree
- 1. 二叉查找树BST的性质
- 2. 二叉搜索树的实现
- 3. 平衡二叉查找树:AVL树的定义
- 4. 保持AVL树的平衡性质
- 七、ADT Map实现方法小结
一、树
- 树是一种非线性的数据结构,一般数据结构的图示把根放在上方,叶放在下方。
- 树是一种分层结构,越接近顶部的层越普遍,越接近底部的层越独特。
- 分类树的第二个特征:一个节点的子节点与另一个节点的子节点相互之间是隔离、独立的。
- 分类树的第三个特征:每一个叶节点都具有唯一性。可以用从根开始到达每个种的完全路径来唯一标识每个物种。
1. 树结构相关术语
- 节点Node:组成树的基本部分,每个节点具有名称,或“键值”,节点还可以保存额外数据项,数据项根据不同的应用而变。
- 边Edge:边是组成树的另一个基本部分。每条边恰好连接两个节点,表示节点之间具有关联,边具有出入方向;每个节点(除根节点)恰有一条来自另一节点的入边;每个节点可以有多条连到其他节点的出边。
- 根Root:树中唯一一个没有入边的节点。
- 路径Path:由边依次连接在一起的节点的有序列表。
- 子节点Children:入边均来自于同一个节点的若干节点,称为这个节点的子节点。
- 父节点Parent:一个节点是其所有出边所连接节点的父节点。
- 兄弟节点Sibling:具有同一个父节点的节点之间称为兄弟节点。
- 子树Subtree:一个节点和其所有子孙节点,以及相关边的集合。
- 叶节点Leaf:没有子节点的节点称为叶节点。
- 层级Level:从根节点开始到达一个节点的路径,所包含的边的数量,称为这个节点的层级。根节点层级为0。
- 高度:树中所有节点的最大层级称为树的高度。
2. 树的定义
2.1 树的定义1
树由若干节点,以及两两连接节点的边组成,并具有以下性质:
- 其中一个节点被设定为根;
- 每个节点n(除根节点),都恰连接一条来自节点p的边,p是n的父节点;
- 每个节点从根开始的路径是唯一的。
- 如果每个节点最多有两个子节点,这样的树称为“二叉树”。
2.2 树的定义2(递归定义)
树是:
- 空集;或者由根节点及0或多个子树构成(其中子树也是树),每个子树的根到根节点具有边相连。
二、实现树
1. 嵌套列表法
-
首先我们尝试用Python List来实现二叉树数据结构。
-
递归的嵌套列表实现二叉树,由具有3个元素的列表实现: [root, left, right]
- 第1个元素为根节点的值;
- 第2个元素是左子树(所以也是一个列表);
- 第3个元素是右子树(所以也是一个列表)。
-
对于二叉树,根是myTree[0],左子树myTree[1],右子树myTree[2]。
-
嵌套列表法的优点:子树的结构与树相同,是一种递归数据结构;很容易扩展到多叉树,仅需要增加列表元素即可。
嵌套列表法代码:
def BinaryTree(r): # 创建仅有根节点的二叉树
return [r, [], []]
def insertLeft(root,newBranch): # 将新节点插入树中作为其直接的左子节点
t = root.pop(1)
if len(t) > 1:
root.insert(1,[newBranch,t,[]])
else:
root.insert(1,[newBranch,[],[]])
return root
def insertRight(root,newBranch): # 将新节点插入树中作为其直接的右子节点
t = root.pop(2)
if len(t) > 1:
root.insert(2,[newBranch,[],t])
else:
root.insert(2, [newBranch, [], []])
return root
def getRootVal(root): # 取得根节点
return root[0]
def setRootVal(root,newVal): # 设置根节点
root[0] = newVal
def getLeftChild(root): # 返回左子树
return root[1]
def getRightChild(root): # 返回右子树
return root[2]
代码运行示例:
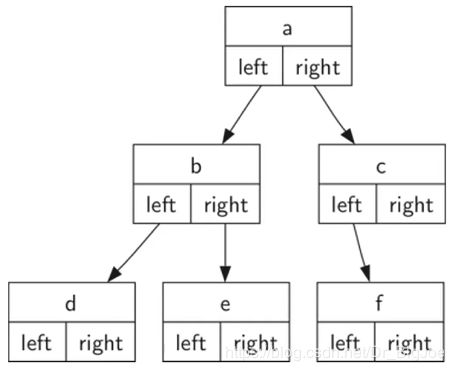
2. 节点链接法
每个节点保存根节点的数据项,以及指向左右子树的链接。
节点链接法代码:
class BinaryTree:
def __init__(self,rootObj):
self.key = rootObj # 成员key保存根节点数据项
self.leftChild = None # 成员leftChild保存指向左子树的引用
self.rightChild = None # 成员rightChild保存指向右子树的引用
def insertLeft(self,newNode):
if self.leftChild == None:
self.leftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
def insertRight(self,newNode):
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def setRootVal(self,obj):
self.key = obj
def getRootVal(self):
return self.key
代码运行示例:
三、树的应用:表达式解析
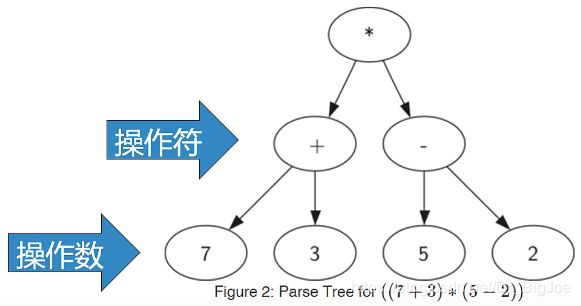
- 可以将表达式表示为树结构,叶节点保存操作数,内部节点保存操作符。
- 表达式层次决定计算的优先级,越底层的表达式,优先级越高。例如全括号表达式:((7+3)*(5-2))
- 树中的每个子树都表示一个子表达式。将子树替换为子表达式值的节点,即可实现求值。
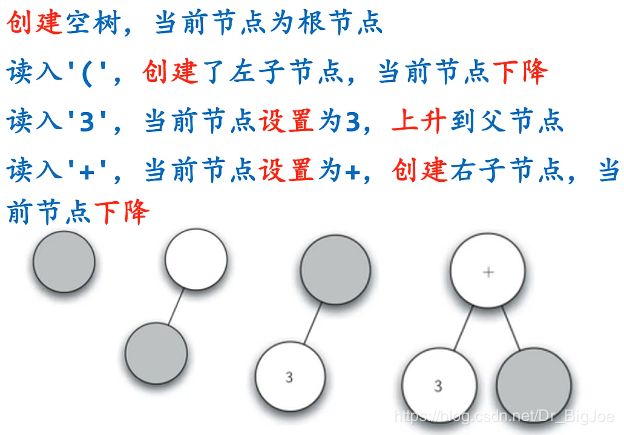
1. 创建表达式解析树:过程
2. 建立表达式解析树:规则
从左到右扫描全括号表达式的每个单词,依据规则建立解析树。
-
如果当前单词是 “(”:为当前节点添加一个新节点作为其左子节点,当前节点下降为这个新节点;
-
如果当前单词是操作符 “+, -, *, /”:将当前节点的值设为此符号,为当前节点添加一个新节点作为其右子节点,当前节点下降为这个新节点;
-
如果当前单词是操作数:将当前节点的值设为此数,当前节点上升到父节点;
-
如果当前单词是 “)”:则当前节点上升到父节点。
3. 建立表达式解析树:思路
创建树过程中关键的是对当前节点的跟踪,我们可以用一个栈来记录跟踪父节点。当前节点下降时,将下降前的节点push入栈;当前节点需要上升至父节点时,上升到pop出栈的节点即可。
建立表达式解析树代码实现:
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree('')
pStack.push(eTree) # 入栈下降
currentTree = eTree
for i in fplist:
if i == '(': # 表达式开始
currentTree.insertLeft('')
pStack.push(currentTree) # 入栈下降
currentTree = currentTree.getLeftChild()
elif i not in ['+','-','*','/',')']: # 操作数
currentTree.setRootVal(int(i))
parent = pStack.pop() # 出栈上升
currentTree = parent
elif i in ['+','-','*','/']: # 操作符
currentTree.setRootVal(i)
currentTree.insertRight('')
pStack.push(currentTree)
currentTree = currentTree.getRightChild()
elif i == ')': # 表达式结束
currentTree = pStack.pop() # 出栈上升
else:
raise ValueError
return eTree
4. 利用表达式解析树求值:思路
-
由于二叉树BinaryTree是一个递归数据结构,自然可以用递归算法来处理。
-
求值递归函数evaluate,可从树的底层子树开始,逐步向上层求值,最终得到整个表达式的值。
-
求值递归函数evaluate的递归三要素:
- 基本结束条件:叶节点是最简单的子树,没有左右子节点,其根节点的数据项即为子表达式树的值。
- 缩小规模:将表达式树分为左子树、右子树,即为缩小规模。
- 调用自身:分别调用evaluate计算左子树和右子树的值,然后将左右子树的值依根节点的操作符进行计算,从而得到表达式的值。
-
一个增加程序可读性的技巧:函数引用
import operator op = operator.add n = op(1,2)
表达式解析树求值代码实现:
import operator
def evaluate(parseTree):
opers = {'+':operator.add, '-':operator.sub,
'*':operator.mul, '/':operator.truediv}
# 缩小规模:
leftC = parseTree.getLeftChild()
rightC = parseTree.getRightChild()
if leftC and rightC:
fn = opers[parseTree.getRootVal()]
return fn(evaluate(leftC),evaluate(rightC)) # 递归调用
else:
return parseTree.getRootVal() # 基本结束条件
四、树的遍历Tree Traversals
按照对节点访问次序的不同来区分3种遍历:
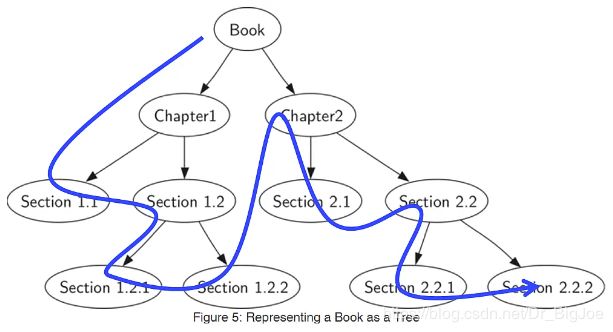
- 前序遍历(preorder):先访问根节点,再递归地前序访问左子树、最后前序访问右子树。
- 中序遍历(inorder):先递归地中序访问左子树,再访问根节点,最后中序访问右子树。
- 后序遍历(postorder):先递归地后续访问左子树,再后续访问右子树,最后访问根节点。
前序遍历的例子:
树的遍历:递归算法代码
# 树的遍历:递归算法代码
# 前序遍历:
def preorder(tree):
if tree:
print(tree.getRootVal())
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
# 后序遍历:
def postorder(tree):
if tree:
postorder(tree.getLeftChild())
postorder(tree.getRightChild())
print(tree.getRootVal())
# 中序遍历:
def inorder(tree):
if tree:
inorder(tree.getLeftChild())
print(tree.getRootVal())
inorder(tree.getRightChild())
在BinaryTree类里实现前序遍历,需要加入子树是否为空的判断:
def preorder(self):
print(self.key)
if self.leftChild:
self.leftChild.preorder()
if self.rightChild:
self.rightChild.preorder()
后序遍历:表达式求值
# 后序遍历:表达式求值
def postordereval(tree):
opers = {'+':operator.add, '-':operator.sub,
'*':operator.mul, '/':operator.truediv}
res1 = None
res2 = None
if tree:
res1 = postordereval(tree.getLeftChild()) # 左子树
res2 = postordereval(tree.getRightChild()) # 右子树
if res1 and res2:
return opers[tree.getRootVal()](res1,res2) # 根节点
else:
return tree.getRootVal()
五、优先队列Priority Queue
-
队列有一种变体称为“优先队列”。优先队列的出队跟队列一样从队首出队;
-
但在优先队列内部,数据项的次序却是由“优先级”来确定:
1. 高优先级的数据项排在队首,而低优先级的数据项排在后面。
2. 这样,优先队列的入队操作就比较复杂,需要将数据项根据其优先级尽量挤到队列前方。
- 实现优先队列的经典方案是采用二叉堆数据结构,二叉堆能够将优先队列的入队和出队复杂度都保持在O(logn)。
- 二叉堆的有趣之处在于,其逻辑结构上像二叉树,却是用非嵌套的列表来实现的。
- 最小key排在队首的称为“最小堆min heap”;反之,最大key排在队首的是“最大堆max heap”。
1. 用非嵌套列表实现二叉堆
-
为了使堆操作能保持在对数水平上,就必须采用二叉树结构。
-
同样,如果要使操作始终保持在对数数量级上,就必须始终保持二叉树的平衡,树根左右子树拥有相同数量的节点。
-
或者采用“完全二叉树”的结构来近似实现平衡。完全二叉树,叶节点最多只出现在最底层和次底层,而且最底层的叶节点都连续集中在最左边,每个内部节点都有两个子节点,最多可有1个节点例外。
-
完全二叉树由于其特殊性,可以用非嵌套列表以简单的方式实现,如下图:如果节点的下标为p,那么其左子节点下标为2p,右子节点为2p+1,其父节点下标为p//2。
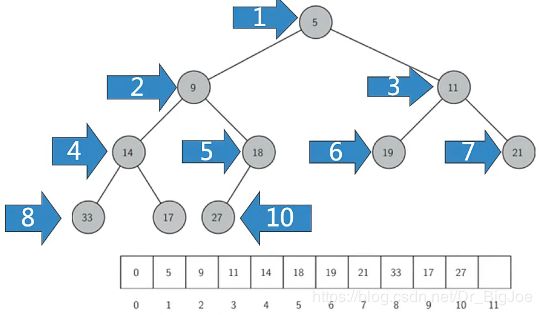
2. 堆次序Heap Order
任何一个节点x,其父节点p中的key均小于x中的key。这样,符合“堆”性质的二叉树,其中任何一条路径,均是一个已排序数列,根节点的key最小。
3. 二叉堆操作的实现
-
二叉堆初始化,采用一个列表来保存堆数据,其中表首下标为0的项无用,但为了后面代码可以用到简单的整数乘除法,仍保留它。
-
insert(key)方法:首先,为了保持完全二叉树的性质,新key应该添加到列表末尾。新key加在列表末尾,显然无法保持堆次序,虽然对其它路径的次序没有影响,但对于其到根的路径可能破坏次序。需要将新key沿着路径来“上浮”到其正确位置。注意:新key的上浮不会影响其他路径节点的堆次序。
-
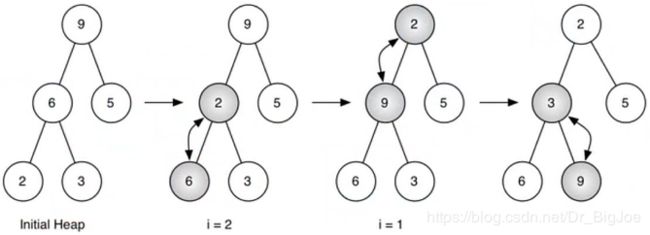
delMin()方法:移走整个堆中最小的key,根节点heapList[1],为了保持完全二叉树的性质,只用最后一个节点来代替根节点。同样,这操作还是破坏了堆次序。解决方法:将新的根节点沿着一条路径下沉,直到比两个子节点都小。下沉的路径选择:如果比子节点大,那么选择较小的子节点交换下沉。
-
buildHeap(lst)方法:从无序表生成堆。用下沉法,能将总代价控制在O(n)。
代码实现:
# 二叉堆操作的实现
class BinHeap:
def __init__(self):
self.heapList = [0]
self.currentSize = 0
def percUp(self,i):
while i//2 > 0:
if self.heapList[i] < self.heapList[i//2]:
temp = self.heapList[i//2]
self.heapList[i//2] = self.heapList[i] # 与父节点交换
self.heapList[i] = temp
i = i//2 # 沿路径向上
def insert(self,k):
self.heapList.append(k) # 添加到末尾
self.currentSize = self.currentSize + 1
self.percUp(self.currentSize) # 新key上浮
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapList[i] > self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc] # 交换下沉
self.heapList[mc] = tmp
i = mc # 沿路径向下
def minChild(self,i):
if i*2 + 1 > self.currentSize:
return i*2 # 唯一子节点
else:
if self.heapList[i*2] < self.heapList[i*2+1]:
return i*2
else: # 返回较小的
return i*2+1
def delMin(self):
retval = self.heapList[1] # 移走堆顶
self.heapList[1] = self.heapList[self.currentSize]
self.currentSize = self.currentSize - 1
self.heapList.pop()
self.percDown(1) # 新顶下沉
return retval
def buildHeap(self,alist):
i = len(alist) // 2 # 从最后节点的父节点开始,因叶节点无需下沉
self.currentSize = len(alist)
self.heapList = [0] + alist[:]
print(len(self.heapList),i)
while (i > 0):
print(self.heapList,i)
self.percDown(i)
i = i-1
print(self.heapList,i)
六、二叉查找树Binary Search Tree
1. 二叉查找树BST的性质
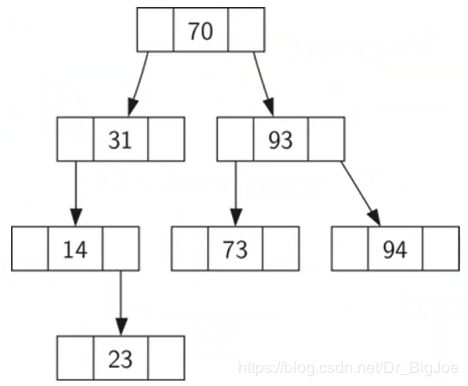
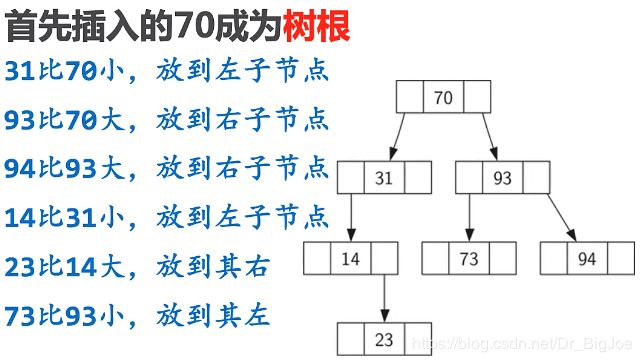
- 比父节点小的key都出现在左子树,比父节点大的key都出现在右子树。
- 按照70,31,93,94,14,23,73的顺序插入。注意:插入顺序不同,生成的BST也不同。
2. 二叉搜索树的实现
-
put(key,val)方法:插入key构造BST。首先看BST是否为空,如果一个节点都没有,那么key成为根节点root,否则,就调用一个递归函数_put(key, val, root)来放置key。
-
_put(key,val,self.root)的流程:如果key比currentNode小,那么_put到左子树,但如果没有左子树,那么key就成为左子节点;如果key比currentNode大,那么_put到右子树,但如果没有右子树,那么key就成为右子节点。
-
BST.get方法:在树中找到key所在的节点取到payload。
-
TreeNode类中的__iter__迭代器,迭代器函数中用了for迭代,实际上是递归函数,yield是对每次迭代的返回值。
-
BST.delete方法:用_get找到要删除的节点,然后调用remove来删除,找不到则提示错误。
-
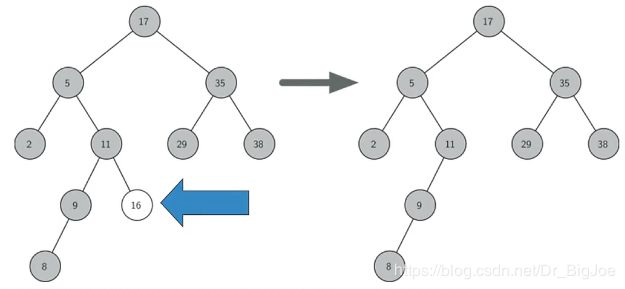
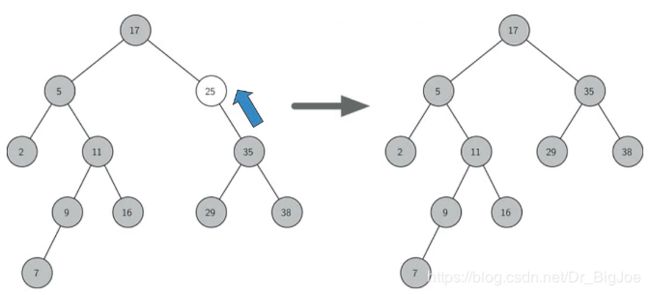
从BST中remove一个节点,还要求仍然保持BST的性质,分以下三种情况:这个节点没有子节点;这个节点有1个子节点;这个节点有2个子节点。
-
被删节点有1个子节点,解决方法:将这个唯一的子节点上移,替换掉被删节点的位置。
代码实现:
class BinarySearchTree:
def __init__(self):
self.root = None
self.size = 0
def length(self):
return self.size
def __len__(self):
return self.size
def __iter__(self):
return self.root.__iter__()
def put(self,key,val):
if self.root:
self._put(key,val,self.root)
else:
self.root = TreeNode(key,val)
self.size = self.size + 1
def _put(self,key,val,currentNode):
if key < currentNode.key:
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild) # 递归左子树
else:
currentNode.leftChild = TreeNode(key,val,parent=currentNode)
else:
if currentNode.hasRightChild():
self._put(key,val,currentNode.rightChild) # 递归右子树
else:
currentNode.rightChild = TreeNode(key,val,parent=currentNode)
def __setitem__(self, k, v):
self.put(k,v)
def get(self,key):
if self.root:
res = self._get(key,self.root) # 递归函数
if res:
return res.payload # 找到节点
else:
return None
else:
return None
def _get(self,key,currentNode):
if not currentNode:
return None
elif currentNode.key == key:
return currentNode
elif key < currentNode.key:
return self._get(key,currentNode.leftChild)
else:
return self._get(key,currentNode.rightChild)
def __getitem__(self, key):
return self.get(key)
def __contains__(self, key):
if self._get(key,self.root):
return True
else:
return False
def delete(self, key):
if self.size > 1:
nodeToRemove = self._get(key, self.root)
if nodeToRemove:
self.remove(nodeToRemove)
self.size = self.size - 1
else:
raise KeyError('Error, key not in tree')
elif self.size == 1 and self.root.key == key:
self.root = None
self.size = self.size - 1
else:
raise KeyError('Error, key not in tree')
def __delitem__(self,key):
self.delete(key)
def remove(self,currentNode):
if currentNode.isLeaf(): #leaf
if currentNode == currentNode.parent.leftChild:
currentNode.parent.leftChild = None
else:
currentNode.parent.rightChild = None
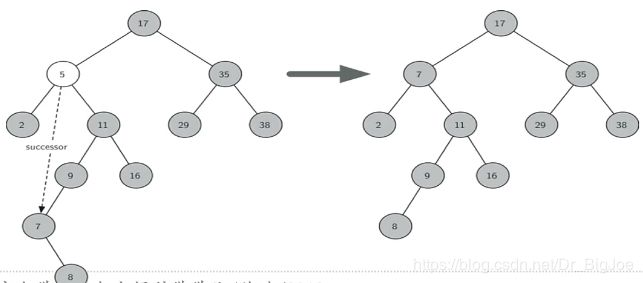
elif currentNode.hasBothChildren(): #interior
succ = currentNode.findSuccessor()
succ.spliceOut()
currentNode.key = succ.key
currentNode.payload = succ.payload
else: # this node has one child
if currentNode.hasLeftChild():
if currentNode.isLeftChild(): # 左子节点删除
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.leftChild
elif currentNode.isRightChild(): # 右子节点删除
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.leftChild
else: # 根节点删除
currentNode.replaceNodeData(currentNode.leftChild.key,
currentNode.leftChild.payload,
currentNode.leftChild.leftChild,
currentNode.leftChild.rightChild)
else:
if currentNode.isLeftChild(): # 左子节点删除
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.rightChild
elif currentNode.isRightChild(): # 右子节点删除
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.rightChild
else: # 根节点删除
currentNode.replaceNodeData(currentNode.rightChild.key,
currentNode.rightChild.payload,
currentNode.rightChild.leftChild,
currentNode.rightChild.rightChild)
class TreeNode:
def __init__(self,key,val,left=None,right=None,parent=None):
self.key = key # 键值
self.payload = val # 数据项
self.leftChild = left # 左子节点
self.rightChild = right # 右子节点
self.parent = parent # 父节点
def hasLeftChild(self):
return self.leftChild
def hasRightChild(self):
return self.rightChild
def isLeftChild(self):
return self.parent and self.parent.leftChild == self
def isRightChild(self):
return self.parent and self.parent.rightChild == self
def isRoot(self):
return not self.parent
def isLeaf(self):
return not (self.rightChild or self.leftChild)
def hasAnyChildren(self):
return self.rightChild or self.leftChild
def hasBothChildren(self):
return self.rightChild and self.leftChild
def replaceNodeData(self,key,value,lc,rc):
self.key = key
self.payload = value
self.leftChild = lc
self.rightChild = rc
if self.hasLeftChild():
self.leftChild.parent = self
if self.hasRightChild():
self.rightChild.parent = self
def findSuccessor(self):
succ = None
if self.hasRightChild():
succ = self.rightChild.findMin()
else:
if self.parent:
if self.isLeftChild():
succ = self.parent
else:
self.parent.rightChild = None
succ = self.parent.findSuccessor()
self.parent.rightChild = self
return succ
def findMin(self):
current = self
while current.hasLeftChild(): # 到左下角
current = current.leftChild
return current
def spliceOut(self):
if self.isLeaf():
if self.isLeftChild(): # 摘出叶节点
self.parent.leftChild = None
else:
self.parent.rightChild = None
elif self.hasAnyChildren():
if self.hasLeftChild():
if self.isLeftChild():
self.parent.leftChild = self.leftChild
else:
self.parent.rightChild = self.leftChild
self.leftChild.parent = self.parent
else:
if self.isLeftChild():
self.parent.leftChild = self.rightChild # 摘出带右子节点的节点
else:
self.parent.rightChild = self.rightChild
self.rightChild.parent = self.parent
# 中序遍历的迭代:
def __iter__(self):
if self:
if self.hasLeftChild():
for elem in self.leftChild:
yield elem
yield self.key
if self.hasRightChild():
for elem in self.rightChild:
yield elem
3. 平衡二叉查找树:AVL树的定义
-
AVL树能在key插入时一直保持平衡。AVL是发明者名字的缩写。
-
AVL树的实现中,需要对每个节点跟踪“平衡因子 balance factor”参数。
-
平衡因子是根据节点的左右子树的高度来定义的,确切地说,是左右子树的高度差:balanceFactor = height(leftSubTree) - height(rightSubTree)。如果平衡因子大于0,称为“左重left-heavy”,小于零称为“右重right-heavy”,平衡因子等于0,则称作平衡。
-
如果一个二叉查找树中每个节点的平衡因子都在-1, 0, 1之间,则把这个二叉搜索树称为平衡树。
-
在平衡树操作过程中,有节点的平衡因子超出此范围,则需要一个重新平衡的过程。
分析AVL树最差情况下的性能:
-
即平衡因子为1或者-1。下图为平衡因子为1的左重AVL树,树的高度从1开始,来看看问题规模(总节点数N)和比对次数(树的高度h)之间的关系如何?
-
观察上图h = 1~4时,总节点数N的变化:
h = 1, N = 1
h = 2, N = 2 = 1+ 1
h = 3, N = 4 = 1 + 1 + 2
h = 4, N = 7 = 1 + 2 + 4
可得通式:Nh = 1 + Nh-1 + Nh-2 ,观察这个通式,很接近斐波那契。
对上图打红色问号的式子存在疑问,两边同时取对数,等号左边应该是log(Nh + 1)才对啊,希望有大神看到能为我解答困惑!
4. 保持AVL树的平衡性质
-
首先,作为BST,新key必定以叶节点形式插入到AVL树中。
-
叶节点的平衡因子是0,其本身无需重新平衡,但会影响其父节点的平衡因子:作为左子节点插入,则父节点平衡因子会增加1;作为右子节点插入,则父节点平衡因子会减少1.
-
这种影响可能随着其父节点到根节点的路径一直传递上去,直到:传递到根节点为止;或者某个父节点的平衡因子被调整到0,不再影响上层节点的平衡因子为止。
rebalance重新平衡:
- 主要手段:将不平衡的子树进行旋转rotation。视左重或者右重进行不同方向的旋转,同时更新相关父节点引用,更新旋转后被影响节点的平衡因子。
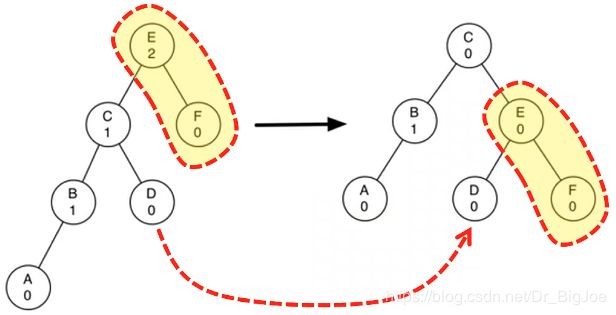
-
如上图,是一个右重子树A的左旋转(并保持BST性质)。将右子节点B提升为子树的根,将旧根节点A作为新根节点B的左子节点;如果新根节点B原来有左子节点,则将此节点设置为A的右子节点(A的右子节点一定有空)。
-
更复杂的情况:如下图左重的子树右旋转。旋转后,新根节点将旧根节点作为右子节点,但是新根节点原来已有右子节点,需要将原有的右子节点重新定位;原有的右子节点D改到旧根节点E的左子节点,同样,E的左子节点在旋转后一定有空。
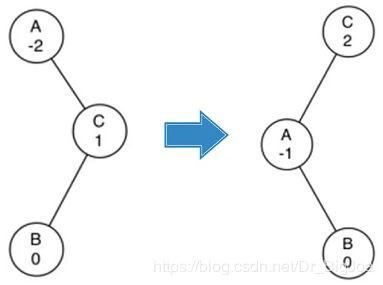
- 左旋转对平衡因子的影响:
- 下图右重子树,单纯的左旋转无法实现平衡,左旋转后变成左重了,左重再右旋转,还回到右重。
- 所以,在左旋转之前检查右子节点的因子,如果右子节点左重的话,先对它进行右旋转,再实施原来的左旋转;同样,在右旋转之前检查左子节点的因子,如果左子节点右重的话,先对它进行左旋转,再实施原来的右旋转。
AVL树算法代价:
- 经过复杂的put方法,AVL树始终维持平衡,get方法也始终保持O(logn)高性能。
- 将AVL树的put方法分为两个部分:需要插入的新节点是叶节点,更新其所有父节点和祖先节点的代价最多为O(logn),如果插入的新节点引发了不平衡,重新平衡最多需要两次旋转,但旋转的代价与问题规模无关,旋转代价是常数O(1)。所以整个put方法的时间复杂度还是O(logn)。
七、ADT Map实现方法小结
推荐使用散列表和AVL树。
==================================================================
以上均为个人学习笔记总结,学习代码见week18
课程名称:数据结构与算法Python版_北京大学_中国大学MOOC(慕课)
课程主页: http://gis4g.pku.edu.cn/course/pythonds/