自动驾驶之无人驾驶车辆与模型预测控制
无人驾驶车辆
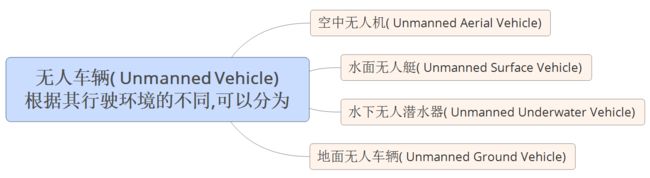
无人车辆( Unmanned Vehicle),根据其行驶环境的不同,可以分为空中无人机( Unmanned Aerial Vehicle)、水面无人艇( Unmanned Surface Vehicle)、水下无人潜水器( Unmanned Underwater Vehicle)和地面无人车辆( Unmanned Ground Vehicle)。
补充:
遥操作无人车辆不等同于完全的遥控车辆,而是在自主行驶无人车辆基础上**,增加了人在回路的任务决策、环境感知与规划、控制等功能**,是一种提升自主无人车辆控制能力的人机交互方式,或者被称为人在回路的决策、规划与控制方法
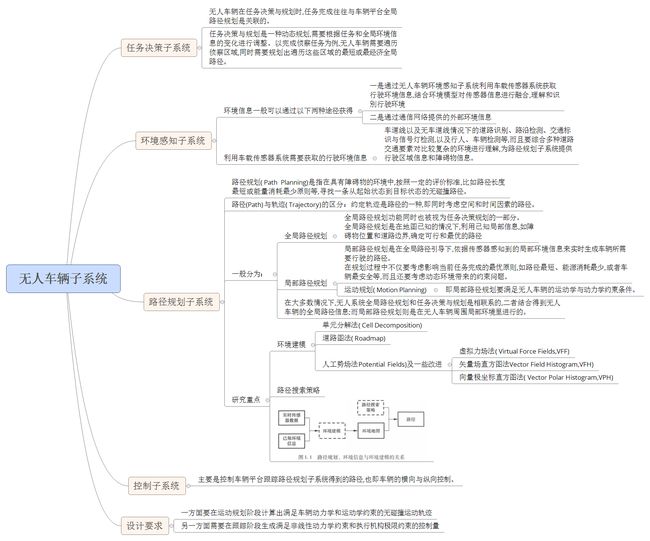
无人车辆系统分为任务决策、环境感知、路径规划,以及车辆控制与平台4个子系统。
(1)任务决策子系统
无人车辆在任务决策与规划时,任务完成往往与车辆平台全局路径规划是关联的。
任务决策与规划是一种动态规划,需要根据任务和全局环境信息的变化进行调整。以完成侦察任务为例,无人车辆需要遍历侦察区域,同时需要规划出遍历这些区域的最短或最经济全局路径。
(2)环境感知子系统
环境信息一般可以通过以下两种途径获得:一是通过无人车辆环境感知子系统利用车载传感器系统获取行驶环境信息,结合环境模型对传感器信息进行融合,理解和识別行驶环境;二是通过通信网络提供的外部环境信息,例如车联网给无人驾驶车辆提供的前方道路拥堵情况和周围车辆行驶趋势,路基交通设施发送的路口交通信号灯情况和变化趋势,或者地面指挥系统给无人机提供的大范围空域环境信息。
环境感知是无人车辆可靠行驶的关键。
以行驶在城市环境的无人驾驶车辆为例,如果不依赖外部网络提供的环境信息,独立的无人驾驶车辆需要识别行驶道路及与交通规则相关的各类环境信息,包括车道线以及无车道线情况下的道路识别、路沿检测、交通标识与信号灯检测,以及行人、车辆检测等,而且要综合多种道路交通要素对比较复杂的环境进行理解,为路径规划子系统提供行驶区域信息和障碍物信息。
(3)路径规划子系统
路径规划( Path Planning)是指在具有障碍物的环境中,按照一定的评价标准,比如路径长度最短或能量消耗最少原则等,寻找一条从起始状态到目标状态的无碰撞路径。
一般分为全局路径规划和局部路径规划。
全局路径规划功能同时也被视为任务决策规划的一部分。在大多数情况下,无人系统全局路径规划和任务决策与规划是相联系的,二者结合得到无人车辆的全局路径信息;而局部路径规划则是在无人车辆周围局部环境里进行的。全局路径规划是在地图已知的情况下,利用已知局部信息,如障碍物位置和道路边界,确定可行和最优的路径;但是当环境发生变化,如出现未知障碍物时,就必须通过局部路径规划来生成无人车辆的局部行驶路径或轨迹。
局部路径规划是在全局路径引导下,依据传感器感知到的局部环境信息来实时生成车辆所需要行驶的路径。在规划过程中不仅要考虑影响当前任务完成的最优原则,如路径最短、能源消耗最少,或者车辆最安全等,而且还要考虑动态环境带来的约束问题。
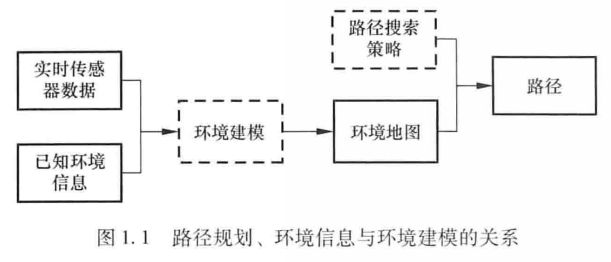
路径规划技术的研究重点主要包括环境建模和路径搜索策略两个子问题,如图1.1所示。
路径规划与障碍物环境信息密切相关,因此障得物环境的建模方法是路径规划问题研究中的一个关键问题。目前,最常用的3种环境建模方法是单元分解法( Cell Decomposition)、道路图法( Roadmap)和人工势场法Potential Fields)。
其中人工势场法在实时避障方面具有独特优势。在此基础上,又提出了虚拟力场法( Virtual Force Fields,VFF)、矢量场直方图法Vector Field Histogram,VFH)和向量极坐标直方图法( Vector Polar Histogram,VPH)。这些方法在机器人和无人车辆障得规避方面得到大量应用。
局部路径规划过程中,还需要考虑的一个重要问题是运动规划( Motion Planning),即局部路径规划要满足无人车辆的运动学与动力学约束条件。
文献[16]提出的满足无人车辆运动微分约束的纵横向协同规划算法就是一种典型的局部路径规划的运动规划方法。
[16]姜岩,龚建伟,熊光明,陈慧岩.基于运动微分约束的无人车辆纵横向协同规划算法的研究[J].自动化学报,2013,39(12):2012-2020
将模型预测控制理论应用在无人车辆运动规划时,也将重点探索该方法在处理运动学和动力学约束的途径。
(4)车辆平台控制子系统
车辆控制主要是控制车辆平台跟踪路径规划子系统得到的路径,也即车辆的横向与纵向控制。
和机器人控制一样,无人车辆也存在着路径(Path)与轨迹( Trajectory)的区分。约定轨迹是路径的一种,即同时考虑空间和时间因素的路径。
路径跟踪实质是通过控制车辆的运动来减少车辆与参考路径之间的空间上的误差。如果考虑轨迹,则还包括时间误差。因模型预測控制重点应用在跟踪控制方法中,后续章节将继续对这一点进行详细说明。
设计要求
车辆平台是无人车辆的重要组成部分。环境感知、决策规划及控制必须与车辆平台进行一体化设计。各种无人车辆在行驶环境中,以较高速度行驶时,都会与环境发生相互作用,这时车辆动力学与运动学特性就会影响到环境感知、决策规刘和控制效果。以最为复杂的地面无人车辆为例,高速行驶的车辆执行机构的控制输入、轮胎与地面摩擦引起的滑移、横向加速度引起的侧倾等动力学非线性约束条件比低速时更加苛刻。
因此,无人车辆一方面要在运动规划阶段计算出满足车辆动力学和运动学约束的无碰撞运动轨迹,另一方面需要在跟踪阶段生成满足非线性动力学约束和执行机构极限约束的控制量。
考虑乘坐舒适性的无人驾驶车辆
选择有人乘坐的无人驾驶车辆( Self-driving Vehicle)的原因:这类车辆的运动学模型和动力学模型都比较成熟,在仿真软件 Carsim和 Adams中都有相应的模型,便于我们重点介绍模型预測控制理论在无人驾驶车辆控制中的应用。
路径跟踪( Path Following)与轨迹跟踪( Trajectory Tracking)
路径规划和轨迹规划
无人车辆也存在着路径(
Path)与轨迹(Trajectory)的区分。约定轨迹是路径的一种,即同时考虑空间和时间因素的路径。
路径与轨迹延续了机器人控制的概念。
对于无人车辆来说,全局路径点只要包含空间位置信息即可,也可以包含姿态信息,而不需要与时间相关,但局部规划时,则可以考虑时间信息。
这里规定轨迹点也是一种路径点,即当路径点信息中加入了时间约束,就可以被称为轨迹点。
从这个角度理解,轨迹规划就是一种路径规划,当路径规划过程要满足无人车辆的纵向和横向动力学约束时,就成为轨迹规划。
路径规划与轨迹规划既可以在状态空间中表示,也可以在笛卡尔坐标系中表示。
状态空间中表示:
[15]张浩杰,龚建伟,姜岩,熊光明,陈慧岩.基于变维度状态空间的增量启发式路径规划方法研究「J].自动化学报,2013,39(10):1602-1610
笛卡尔坐标系中表示:
[16]姜岩,龚建伟,熊光明,陈慧岩.基于运动微分约束的无人车辆纵横向协同规划算法的研究[J].自动化学报,2013,39(12):2012-2020
文献[16]提出一种基于运动微分约束的无人车辆纵、横向协同规划算法,实际上考虑了无人车辆通过某一路径点的速度要求,是一种轨迹规划算法。
无人车辆纵向速度规划与时间密切相关,而车辆横向动力学对纵向速度的影响非常大。
路径跟踪和轨迹跟踪
路径跟踪过程中,参考路径( Reference Path)曲线可与时间参数无关,跟踪控制时,可以假设无人车辆以当前速度匀速前进,以一定的代价规则形成行驶路径趋近于参考路径;
而轨迹跟踪时,参考路径曲线与时间和空间均相关,并要求无人车辆在规定的时间内到达某一预先设定好的参考路径点。
路径跟踪不同于轨迹跟踪,不受制于时间约束,只需要在一定误差范围内跟踪期望路径。路径跟踪中的运动控制就是寻找一个有界的控制输入序列,以使无人车辆从一个初始位形到设定的期望位形。
文献「26]指出,无人车辆系统是一个欠驱动的非完整约束系统,同时也是一个零动力学系统。轨迹跟踪问题会受限于这种不稳定的零动力学约束。
[ 26 ] Hilgert J , Hirsch K , Bertram T , et al . Emergency Path Planning for Autonomous Vehicles Using Elastic Band Theory [ C ] . IEEE / ASME International Conference on Advanced Intelligent Mechatronics , 2003 ( 2 ) : 1390-1395
模型预测控制在无人驾驶车辆运动规划与控制中的应用
车辆动力学模型分析对于解决无人驾驶车辆运动规划与控制问题的作用:
- 首先,在规划与控制系统中引入动力学模型可以通过模型的等效约束转化减少规划与控制的计算量,提高系统的实时性。
- 其次,以准确的动力学模型作为预测模型,可以提高控制器对车辆未来行为的预测能力,进而在保证车辆稳定运行的同时,充分发挥车辆的机动潜能,比如高速运行状况下的主动危险规避运动规划与控制,充分体现车辆平台运动学与动力学约束条件的影响。
模型预测控制最明显的优点是能在控制过程中增加多种约束。
无人车辆在低速时,车辆平台运动学约束影响较大,而随着速度的增加,动力学特性对运动规划与控制的影响就越明显,带来多种模式的约束。这正是模型预测控制在无人车辆运动规划控制方面的应用优势。
运动规划算法的模型约束
一旦轨迹被确定了,车辆沿着路径的运动形式也就被确定了。轨迹规划既可以是在路径规划后的二次规划,也可以根据感知信息一次规划获得。
(1)路径规划算法约束条件
无人驾驶车辆的局部路径规划算法不同于一般移动机器人的路径规划问题。为满足车辆转向过程中的平稳性以及安全性需求,车辆运动微分约束和动力学特性约束是需要考虑的重要特征,同时还需要考虑车辆操纵稳定性及舒适性问题带来的控制约束。
文献[26]利用弹性带理论( Elastic Band Theory)对无人驾驶车辆的紧急避障路径进行规划,在规划时提出将路径的局部曲率变化最小作为约束条件,从而提高车辆紧急避障时的操纵稳定性。
[26]Hilgert J , Hirsch K , Bertram T , et al . Emergency Path Planning for Autonomous Vehi -les Using Elastic Band Theory [ C ] . IEEE / ASME International Conference on AdvancedIntelligent Mechatronics , 2003 ( 2 ) : 1390-1395
文献[27]讨论了非结构化环境下基于滚动窗口的无人车辆路径规划问题,并在规划过程中考虑了车辆的安全约束。
[27]Schouwenaars T , How J , FERON E . Receding Horizon Path Planning with Implicit SafetyGuarantees [ C ] . Proceedings of the American Control Conference , 2004 ( 1 ) : 55765583
局部路径规划算法中考虑约束的一种思路是对车辆行驶曲线进行描全局或局部环境参考路径述,通过设计评价函数选取不同工况下的行驶曲线完成规划。
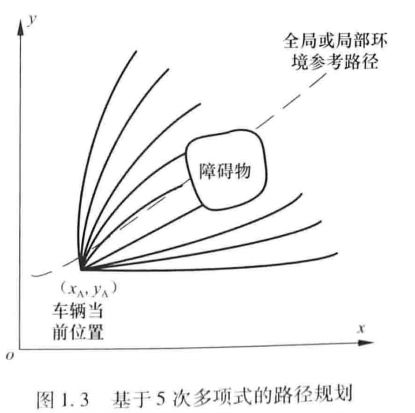
文献[16]利用5次多项式描述行驶曲线,将障碍物题变为求取连接两个确定的目标点之间的曲线,并且满足目标点处有固定的航向角和固定曲率的要求,如图1.3所示;
同时,在全局或者局部环车辆当境中的参考路径上用不同预瞄距离确前位置定若干个预瞄位姿,对于每个预瞄位姿沿其法线方向按照不同横向位置图1.3基于5次多项式的路径规划差再确定若干个目标位姿,各目标位姿航向与预瞄位姿相同,计算当前车辆位交和各目标位姿之间的行驶曲线作为候选曲线集合,行驶曲线需要满足车辆运动微分约束。
候选曲线集合包含了用不同预瞄距离生成的行驶曲线,而对于同预瞄距离处的多条行驶曲线,其目标位姿相对于期望路径是对称分布的。首先对各条行驶曲线进行碰撞分析,在行驶曲线上的每一位姿处增加车辆的宽度和长度信息,与构形空间中的障碍物检測结果进行对比,判断行驶曲线与障碍物发生碰撞的位置,仅保留此位置以前的行驶曲线。
然后,在具有相同横向位置偏差的行驶曲线中保留最长的一条用于路径评价。经过碰撞安全性分析,在每个横向位置偏差仅保留了一条满足横向安全和路径跟踪要求的行驶曲线。车辆的实际驾驶行为,如跟随或超车,则由选择哪一条行驶曲线作为待执行路径实现。
[16]姜岩,龚建伟,熊光明,陈慧岩.基于运动微分约束的无人车辆纵横向协同规划算法的研究[J].自动化学报,2013,39(12):2012-2020
文献[28]德国卡尔斯鲁厄大学在 DARPA可行驶触须 Urban Challenge的参赛车辆AnieWAY上采用了基于触须原理的局部路径规划算法(,利用多组不同半径的圆弧描述不同车速下的行驶路径,如图1.4所示。
[28] Von Hundelshausen F , Himmelsbach M . Hecker F . et al . Driving with Tentacles : Integral Structures for Sensing and Motion [J]. Journal of Field Robotics. 200825(9)640-673
文献[18]对该算法进行了改进,使之适用于全局环境未知的智能车自主行驶,但由于它在进图1.4基于触须的路径规划触须生成时采用圆弧曲线,而忽略了车辆转弯半径的变化,故在车速较快时容易发生跟踪失败的情况。这也说明在高速时还需要进一步考虑车辆动力学特性的约束。
[18]Yu H, Gong J, lagnemma K, Jiang Y, Duan J. Robotic Wheeled Vehicle Ripple Tenta-cles Motion Planning Method [ C]. IEEE Intelligent Vehicles Symposium, 2012(6)1156-1161.
文献[29]结合预测控制理论进行无人车辆的局部路径规划。借鉴预測控制的滚动优化原理,提出了基于滚动窗口的移动机器人路径规划方法。该方法在全局环境未知吋能够充分利用已探知的局部信息,有效地结合优化与反馈机制,不仅使局部规划的计算量保持在较低水平,而且保证了全局的收敛性,获得了较好的规划效果。
[29]张纯刚,席裕庚,动态未知环境下移动机器人的滚动路径规划[J].机器人,2002,24(1):71-75
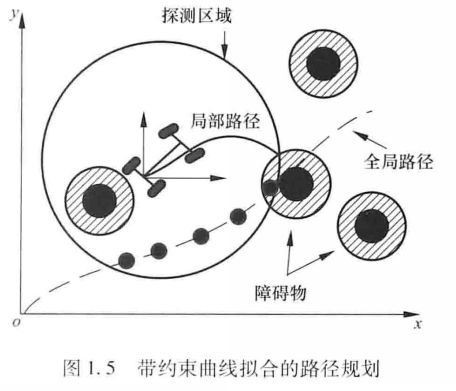
文献[30]同样借鉴了滚动优化的原理,提出了一种带约束曲线拟合的路径规划方式,如图1.5所示。该方法通过在规划中引入几何约束,如起始位姿约束、最小转弯半径约束等,有效地避免了在跟踪过程中同时考虑位置和航向误差的问题。
[30]从岩峰,安向京,陈虹,等.基于滚动优化原理的类车机器人路径跟踪控制[J吉林大学学报:工学版,2012,42(1):182-187
(2)轨迹规划算法约束条件
轨迹规划问题一般是在考虑系统某项性能最优的同时,加入边界约束、环境几何约束以及系统的动力学约束等非线性约束,最终构成一个非线性最优化问题。
因此,轨迹规划的主要研究方向集中在非线性最优求解和约束条件等价转换上。
轨迹规划问题一般无法找到显式解,普遍的做法就是将这一优化问题转换为非线性规划问题,进而通过相应的非线性规划求解器求解。
文献[31]采用直接法,利用多项式直接对系统状态进行参数化,进而将轨迹规划问题转换为数学规划问题。
文献[32]在借鉴样条法原理的基础上,通过局部近似的方法构建全局连续的优化轨迹。虽然这种转换解决了在轨迹空间优化的难题,但是其优化的速度依赖于参数空间的维度。
文献[33]为此, Fahroo等人在对非线性系统平坦性研究的基础上,给出了平坦系统的轨迹规划方法。其主要优点就是通过系统的平坦性将高维度空间的参数优化问题降为低维度参数空间的优化问题,从而提高了优化速度。
文献[34,35]吉林大学陈虹等也应用微分平坦理论对不同形式的机器人进行了轨迹规划方面的研究。
侧倾约束下的运动规划也是高速运动车辆需要考虑的一个重要约束。侧倾主要采用横向载荷转移率(LTR)、侧倾角和横向加速度作为判断标准。
Tahirovic在被动侧翻控制基础上进行了模型预测改进运动规划;
lagneia在机器人车辆运动轨迹规划时**,设计车辆动力学参数值窗口,采用速度一曲率轨迹方法计算运动轨迹**。由于采用窗口值只考虑曲率,所以其计算速度快,但并不具备车辆控制稳定的最优性。
在约束条件处理方面,基于简化运动学模型满足车辆非完整约束的方法比较普遍。假设车辆在运动过程中没有滑移,那么就是非完整( Nonholonomic)动力学约束,但是这种方法不适用于高速行驶车辆,因为此时车辆的约束已经不再局限于非完整约束,车辆的横向动力学成为规划中必须考虑的因素。
文献[39]和[40]在考虑车辆动力学约束情况下对车辆的行驶轨迹进行了规划,实现了连续曲率的轨迹规划。
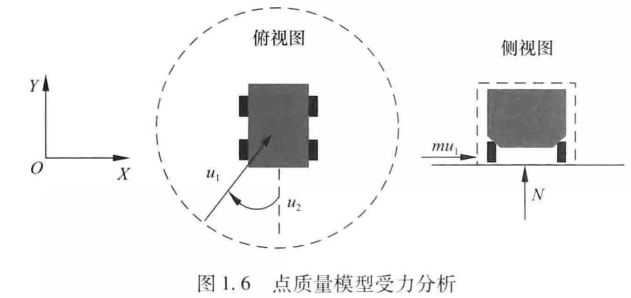
为了减少动力学约束的复杂程度**,忽略车辆尺寸信息简化而来的点质量模型**也在轨迹规划中得到了应用。其受力分析如图1.6所示。从图1.6中可以看出,该模型考虑了车辆的側向受力,并且将约束条件转换为加速度圆( Acceleration Circle Constraint)。应用该模型能够顺利完成避障任务。点质量模型相比于普通自行车模型计算量更小,可以有效地减少车辆非线性动力学模型的复杂性。将车辆动力学模型近似为点质量模型,同时轮胎摩擦圆约束也被映射到加速度约束上,以及其他的一些技巧均可用于简化计算。
(3)运动规划算法及存在的问题小结
从上面可以看出,轨迹规划方面的研究一般都按照局部路径规划方法进行,然后在考虑多种约束条件的情况下对其进行轨迹化。与低速行驶的移动机器人不同的是,无人驾驶车辆的路径和轨迹规划更多采用多项式行驶曲线的方式进行拟合,同时考虑了执行机构的约束。这种规划的特点是能够保证车辆平顺行驶,不会出现突然转向。为了进一步提高系统的实时性,微分平坦、点质量模型等相关理论也被应用在了轨迹规划的过程中。
普通规划方法在高速无人车辆运动规划中普遍存在的问题是实时性达不到要求,特别是紧急情形下的危险规避运动规划对实时性要求更高。基于动力学优化模型的规划方法均考虑了轮胎摩擦圆约束,采用受加速度约束的点质量模型来近似轮胎摩擦圆约束,但没有对高速车辆动力学模型结合运动规划做深入的最优分析。
侧倾约束下的运动规划方法研究较少,且主要集中在越野环境,仅仅是根据阈值窗口范围进行运动规划,也同样没有根据车辆动力学理论的稳定性最优原则产生运动轨迹。此外,同时考虑滑移与侧倾的研究则更少。
点质量模型最优控制特性分析也是运动规划中的一个重要因素。用加速度值有界且方向可控的点质量模型进行最优控制特性分析和证明,能保证建立在此基础上的相关算法的可靠应用。 Bryson和Ho给出了几种情形的证明并且将其应用到运载火箭的发射中,用于推力控制分析,可以供地面车辆的运动规划最优特性分析参考。
轨迹跟踪控制的模型约束
轨迹跟踪控制的主要任务是根据车辆的运动学和动力学约束输出相应的控制参数,如前轮偏角、车轮制动力等。
目前应用较多的控制算法有PID控制算法、滑模控制算法、神经网络控制算法等。
这些方法对参数和环境的依赖程度较高,当环境发生较大变化时不能很好地适应新状态下的轨迹跟踪;同时,地面无人车辆在运动过程中受到运动学约束以及执行机构的约東,在高速运动情况下还需要考虑相应的动力学约東。
上述方法对这些约束难以处理。由于基于模型预测控制的轨迹跟踪算法对未来轨迹的预测和处理多目标约束条件的能力较强,故逐渐成为研究的热点。
在应用车辆模型进行预测时,是否考虑轮胎滑移是一个非常重要的约束条件。这也是实际车辆測试的一个难点问题。轮胎滑移率也是驱动防滑系统(ASR)及防抱死制动系统(ABS)的关键参数。考虑到轮胎柔度和摩擦力饱和值.轮胎纵横向耦合摩擦力(驱动力)模型一般为滑移率的非线性函数。目前应用较广的是 Pacejka提出的魔术公式轮胎模型。
(1)非完整动力学约束轨迹跟踪
非完整( Nonholonomic)动力学约束就是假设车辆在运动过程中没有滑移。很多在平坦路面运动的无人车辆或移动机器人都用这种假设设计轨迹跟踪控制器,特别是纯跟踪算法( Pure Pursuit),已经被成功地应用在很多机器人轨迹跟踪控制中,包括获得2005年 DAPAR沙漠挑战赛冠军的斯坦福大学的Stanlev赛车“
(2)摩擦力与滑移率非线性约束轨迹跟踪
带有纵横向耦合滑移的非线性轮胎模型在轨迹跟踪控制器中一般利用数值优化计算方法进行解算。
文献[46]应用凸二次锥规划优化数值计算方法,而且在控制中使用了非线性耦合模型的简化模型。
文献[47]用预测控制方法为自主车辆设计适应轮胎摩擦极限的轨迹跟踪控制器,应用了耦合非线性轮胎模型。该模型较复杂。 Velenis和 Razzoli通过推导出无人驾驶车辆在转弯时的速度、轮胎侧偏角、横摆角速度等参数,在仿真实验中应用滑模控制方法能很好地控制车辆在漂移状态下行驶“。其主要不足是只能稳定地控制均匀漂移的运动并且还无法跟踪时变曲率轨迹。
[46] Johansson B, Gafvert M. Untripped SUV Rollover Detection and Prevention J). Pro43rd IEEE Conf. Decision and Control, 2004(5): 5461-5466
[47]Falcone P, Borrelli F, Asgari J, et al. Predictive Active Steering Control for AutonomousVehicle Systems [J. IEEE Transactions on Control Systems Technology, 2007, 15(3)
(3)车辆动力学模型简化对模型预测控制的影响
预测模型的选择也是基于模型预测控制的轨迹跟踪算法需要考虑的关键问题之一。使用复杂的模型能够更好地对车辆输出进行预测,但同时也增大了控制器的计算量,实时性难以保证;而使用简单的模型有可能导致跟踪失败。
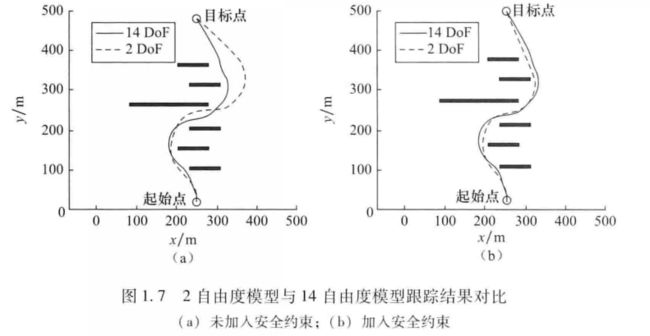
针对这个问题,文献[49]分别基于2自由度自行车模型和14自由度动力学模型设计了轨迹跟踪控制器,然后对轨迹跟踪效果进行对比,结果如图1.7所示。其中,图1.7(a)为没有考虑安全约束,而图1.7(b)中两者都加入安全约束。可以看出,基于14自由度模型的控制器能够具备更好的避障效果;但加入了14自由度模型中的安全约束之后,2自由度模型也能具备相近的效果并且计算时间优势明显。因此,复杂的预测模型并不是最好的选择,对车辆动力学模型进行合理简化并且选择满足行驶工况的约束条件オ是研究的重点。也就是说,在模型预測控制中,模型约束条件能够表达控制对象的真实物理限制即可。
[49] Liu J, Jayakumar P, Overholt J L, et al. The Role of Model Fidelity in Model PredictiveControl Based Hazard Avoidance in Unmanned Ground Vehieles Using LIDAR SensorsC). Proceedings of the ASME Dynamic Systems and Control Conference, 2013: 1-10
上面关于模型复杂度对控制效果的分析为控制过程中的模型简化提供了依据。
文献[50]通过对轮式移动机器人的运动学模型在目标轨迹点附近进行线性化,得到了离散的系统状态空间模型;采用线性模型预测控制算法进行轨迹跟踪,并通过仿真和实车实验分别验证了算法的可靠性。
[50]Kuhne F, Lages WF, et al. Model Predictive Control of a Mobile Robot Using Lineariza-tion [J]. Proceedings of Mechatronics and Robototics, 2004(4): 525-530
文献[51,52]在动力学建模方面,麻省理工学院、斯坦福大学以及韩国釜山国立大学等做了深入的研究。MIT的 Robotic Mobility Group课题组通过微分平坦理论、点质量模型对车辆动力学模型进行合理简化,应用轮胎的摩擦圆约東(如图1.8所示),提高了系统的实时性,实现在高速情况下的地面无人车辆危险规避。
[51] Peters S , Razzoli E , lagnemma K . Differential Flatness of a Front-steered Vehicle withTire Foree Control C ] . Proceedings of the IEEE International Conferenee on Roots andSystems , 2011 : 298-30
[52]Spenko M , Kuroda Y , Dubowsky S , Lagnemma K . Hazard Avoidance for High-speedMobile Robots in Rough Terrain [ J ] . Joumnal of Field Roboties , 2006 , 23 ( 5 ) : 311
轮胎摩擦圆代表轮胎与地面摩擦所能产生的最大牵引力。由于牵引力可以为任意方向,以轮胎与地面接触中心点为圆心,最大牵引力为半径得到的圆,就是轮胎摩擦圆。
**摩擦圆约束是指轮胎与地面摩擦时纵向与横向产生的耦合力必须位于摩擦圆内。车辆转弯、加速、减速时,如果耦合力超出了摩擦圆,车辆就会产生滑移。**轮胎摩擦圆会因为路面的状况、轮胎的接地负荷或者轮胎的性能而改变。例如在冰雪或湿滑的路面,轮胎摩擦圆比在常规路面行驶时小。
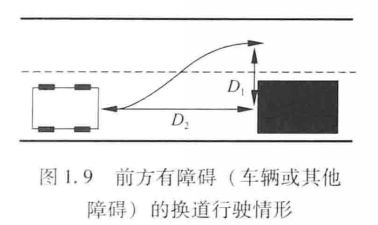
在如图1.9所示的高速车辆换道避障运和特征的摩擦系数F轮胎法向作用力动轨迹规划中, D 2 D_{2} D2是车辆与前方障碍的纵向距离, D 1 D_{1} D1是本车道与旁车道的距离,那么危险规避运动规划问题可表述为:首先计算在满足各轮胎摩擦圆约束和障碍约束的条件下,车辆能够安全换到距离为 D 1 D_{1} D1的车道的最小纵向距离, D 2 m i n D_{2 min} D2min。当调整到 D 2 > D 2 m i n D_{2} > D_{2 min} D2>D2min时,计算车辆换道运动轨迹。
文献53]利用二次锥规划方法来确定作用在车辆上的最优力和力矩。车辆用刚体表示,图1.9前方有障碍(车辆或其他障碍)的换道行驶情形并用由两步优化方法得到的转向和制动命令来控制高阶车辆模型跟踪期望轨迹。
[ 53 ] Hattori Y , Ono E , Hosoe S . Optimum Vehicle Trajectory Control for Obstacle Avoidance
文献[54]Stanford的Crag等在二自由度自行车模型基础上提出了仿射力矩输入模型( Affine Force Input),并将橫摆角速度和轮胎侧偏角约束以包线的形式纳入控制器(如图1.10所示),使车辆能够在极限情况下完成轨迹跟踪,实现车辆性能的最大化利用。
文献[55]则在动力学建模时考虑了车轮转角函数随速度的变化,提高了车辆在高速行驶情况下的控制精度。
[54] Beal C E, Gerdes J C. Model Predictive Control for Vehicle Stabilization at the Iimits ofHandling [J]. IEEE Transactions on Control Systems Technology, 2012: 1-12
[55]Lee J H, Yoo W S. An Improved Model-based Predictive Control of Vehicle Trajectory bUsing Nonlinear Function [J]. Journal of Mechanical Scienee and Technology, 200(4):918-922
(4)微分平坦方法在非线性运动控制模型简化中的应用
微分平坦在无人(空中或地面)车辆或者机器人轨迹跟踪控制中得到了定的关注。微分平坦是一个优化控制问题。从理论上分析,它与全状态反馈线性优化是等价的。
微分平坦系统的定义:如果一个系统能找到平坦输出,使系统的状态和输入都可以用平坦输出及其有限阶导数表示,则该系统被称为平坦系统。
平坦系统的一个好处就是能将非线性系统的微分约束映射为平滑几何约束,有效减少优化空间的维数。对于车辆非线性系统,利用微分平坦输出,能将同时满足运动学约東(速度)和动力学约束(加速度)的 Kinodynamic规划与控制问题简化为计算光滑轨迹的几何规划与控制问题。另外,微分平坦简化模型轨迹跟踪的控制稳定性非常重要。这是滚动优化评价的基础。
文献[51]完成了固定加速度横摆动力学模型在跟踪固定曲率轨迹的控制稳定性分析,但没有涉及时变加速度模型及时变曲率轨迹。
[51] Peters S , Razzoli E , lagnemma K . Differential Flatness of a Front-steered Vehicle withTire Foree Control C ] . Proceedings of the IEEE International Conferenee on Roots andSystems , 2011 : 298-30
(5)侧倾约束对轨迹跟踪控制的影响
原理主要是综合前轮偏角与差动制动方法输入控制量、主动悬架控制技术调整重心位置、发动机扭矩控制与ABS系统结合使用等方法达到防侧倾的目的。
对于在越野环境中运行的车辆或者高速车辆紧急避险转向时侧倾与滑移约束相结合的轨迹跟踪控制稳定性分析是非常重要的。
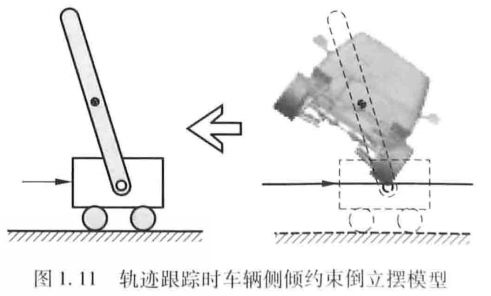
文献[57] lagneia采用能量成形控制( Energy Shaping Control)分析了近似成倒立摆的车辆模型侧倾控制稳定性,借鉴了倒立摆的控制稳定性分析(如图1.11所示)。虽然忽略了横摆滑移非线性,但能量成形控制稳定性方法体现了较好的易用性。
[ 57 ] Peters S , Bobrow J . Lagnemma K . Stabilizing a Vehicle Near Rollover : an Analogy toCart-pole Stabilization [ C ) . IEEE International Conference on Robotics and Automation2010 ( 5 ) : 5194-5200
(6)模型预测控制算法实时性
基于模型预测控制的轨迹跟踪控制器实时性问题:一方面受到所采用动力学模型的影响,另外一方面则是自身计算方式的影响。
目前模型预测控制的基本思想都是在线求解序列二次规划问题,而当系统较为复杂或者约束量比较多时,计算速度不能满足实时控制的需求。
- 提高计算速度的一类方法是将二次规划问题完全用控制量表示,并假定在某一段控制时域内控制量不变。这样可以大大减少优化过程中的变量,从而提高计算速度。
- 另外一种重要的方法被称为“暖启动”,即在每一步开始计算的时候根据上一步的预测结果进行初始化。如果运用得当的话,这种方法将会使总计算次数减少为原来的
1/5。
有学者将前期的一些研究成果进行集成,形成了方便研究者使用的工具箱。
Fast mpc是目前应用较为普遍的快速求解工具箱。它的基本思想是在求解器得到符合目标精度的结果后就提前结束迭代过程,即不再要求每一步计算过程都得到最优解。实验结果表明,应用该工具箱处理含有450个变量和1284个约束条件的复杂系统时,可以达到200Hz的计算速度。- 多参数规划工具箱(
Multi-parametric toolbox,MPT)是一类快速求解线性规划或者二次规划问题的工具箱。其基本原理是通过应用多参数规划方法得到约束最优控制序列与状态之间的显式函数关系,减少规划问题求解的工作量。
(7)轨迹跟踪算法及存在的问题小结
主要突破点为:
- 对动力学模型合理简化,减少控制器的在线计算量,提高控制系统的实时性。
- 对高速情况下的动力学模型进行分析,提高控制系统在车辆高速行驶时的控制精度。
高速车辆在危险障碍规避时的运动轨迹跟踪控制过程中,为保证控制算法满足非线性约束和实时性要求,采用了车辆动力学模型的降维方法;但目前设计的运动轨迹跟踪控制器中大都采用数值优化解算非线性轮胎模型,模型的复杂性增加了计算负担。非线性系统的微分平坦输出特性能有效地将运动轨迹的动力学和运动学Kinodynamic约束映射为几何平滑约束,简化了非线性系统规划与控制计算复杂度,同时将车辆前轮附近的振动中心位置属性作为非线性自行车模型的平坦输出,在高速滑动漂移的运动轨迹跟踪控制中有很好的研究价值。
时变加速度车辆动力学模型(横摆动力学及其他约束等效模型)跟踪时变曲率轨迹的控制稳定性分析尚待突破。