目标检测 记录对AP、mAP、P-R曲线的理解

最初也是看了许多相关知识，总是不理解怎么计算AP、mAP, 借助简单的数字检测识别任务，对AP、mAP尝试计算后，总算是理解了。下面我对计算过程简单进行一个记录。

1. 获取预测结果、Ground_Truth

1.1 数据形式示例

任务：数字（0~9）检测识别

首先需要获取模型对图像的检测结果，如下列形式的数据（一幅图像）：

预测结果:  # [x0, y0, x1, y1, class, score]  
[[171, 199, 206, 252, 1, 0.9266], 
[206, 198, 242, 251, 4, 0.9749], 
[137, 198, 170, 252, 5, 0.8894]] 
Ground_Truth:  #  [x0, y0, x1, y1, class]  
[[133, 197, 168, 251, 5], 
[171, 197, 205, 251, 1],
[208, 197, 243, 251, 4]] 

1.2 检测数据示例

上面只是一幅图像检测结果的举例， 而通常对测试集进行检测，会得到许多预测值：

预测结果如下:  # [x0, y0, x1, y1, class, score]  

[[171, 199, 206, 252, 1, 0.9266], 
[206, 198, 242, 251, 4, 0.9749], 
[137, 198, 170, 252, 5, 0.8894]] 
[207, 106, 286, 198, 1, 0.8885], 
[129, 111, 204, 189, 5, 0.8616], 
[48, 106, 118, 193, 7, 0.9465],
[196, 142, 244, 224, 3, 0.1586], 
[197, 142, 244, 224, 5, 0.3782],
[236, 54, 339, 230, 0, 0.4682], 
[149, 46, 244, 227, 1, 0.21], 
[79, 54, 150, 159, 7, 0.9714], 
[162, 51, 259, 225, 7, 0.9205],
[239, 51, 341, 235, 7, 0.5342]]
...
...

2. 计算精确率P和召回率R

要计算AP先要计算出精确率P和召回率R，某一类的AP就是P-R曲线下的面积。mAP则是所有类别AP的平均值。AP一定是对某一个类别来说的，在以计算类别‘9’的AP为例进行详细计算（测试集中对类别9的框进行提取，结果共有35个检测框）。在得到检测结果后，首先利用预测出来的分类为‘9’的box与其相应Ground_Truth的box计算出交并比Iou。这时，对于每个分类为‘9’的预测框都有了一个交并比Iou值。接下来设定一个交并比阈值th（0.5）,预测框的交并比大于阈值th，则归于正样本，否则归为负样本。

2.1 计算交并比Iou

利用预测出来的分类为‘9’的box与其相应Ground_Truth的box计算出交并比Iou

# 计算IoU例程
# intersection
ixmin = np.maximum(box_gt[0], box_pd[0])
iymin = np.maximum(box_gt[1], box_pd[1])
ixmax = np.minimum(box_gt[2], box_pd[2])
iymax = np.minimum(box_gt[3], box_pd[3])
iw = np.maximum(ixmax - ixmin + 1., 0.)
ih = np.maximum(iymax - iymin + 1., 0.)
inters = iw * ih
# union
uni = ((box_pd[2] - box_pd[0] + 1.) * (box_pd[3] - box_pd[1] + 1.) +
     (box_gt[2] - box_gt[0] + 1.) *
     (box_gt[3] - box_gt[1] + 1.) - inters)
overlaps = inters / uni

2.2 重新划分正负样本

对类别9的35个检测框，计算Iou后并根据阈值th重新划分正负样本，结果如下：
Score：检测框分类为9的置信度
label：根据Iou重新划分的正负样本

2.3 根据预测框的Score排序

进一步根据Score进行排序（由大到小， 如下），此时Iou数据已经用不上了。

2.4 了解基本概念及公式

这时就可以对Score和label数据进行分析了。要计算精确率P和召回率R，得明白下面这些基础概念。

TP(true positive):分类正确，把原本属于正类的样本分成正类。
TN(true negative):分类正确，把原本属于负类的样本分成负类。
FP(false positive):分类错误，把原本属于负类的错分成了正类。
FN(false negative):分类错误，把原本属于正类的错分成了负类。

TP+FP+TN+FN：样本总数。
TP+FN：实际正样本数。
TP+FP：预测结果为正样本的总数，包括预测正确的和错误的。
FP+TN：实际负样本数。
TN+FN：预测结果为负样本的总数，包括预测正确的和错误的。

Recall 即当前被分到正样本类别中，真实的正样本占所有正样本的比例，即召回率（召回了多少正样本比例）；
Precision就是当前划分到正样本类别中，被正确分类的比例（即正式正样本所占比例），就是我们一般理解意义上所关心的正样本的分类准确率；
准确率P就是找得对，召回率R就是找得全

2.5 绘制P-R曲线并计算AP

设定Score阈值为0.6， 这样将类别‘9’的35个检测框结果分为两部分，
第一部分Score>0.6：

第二部分Score<0.6：

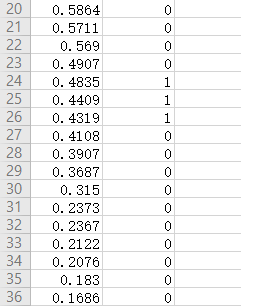
由以上两部分就可以统计出TP、FN、FP、TN，如下表：

精确率P=TP/（TP+FP）=15/（15+3）=0.8333
召回率R=TP/（TP+FN）=15/（15+3）=0.8333

真是巧了，两者相等，举例不太恰当凑合看吧，哈哈，下面是计算单个类别AP的代码

#!/usr/bin/env python
# -*- coding:utf-8 -*- 
# Author: Hren
import csv
import numpy as np
import matplotlib.pyplot as plt

# C9.csv是对检测结果重新划分正负样本后的数据，例：[Score, label]
new_gt_label = []
with open('C9.csv', 'r') as f:
    data = csv.reader(f)
    for i in data:
        new_gt_label.append(i)

score_th = sorted(np.linspace(0.0, 0.999, 50), reverse=True)
pred = []
rec = []
AP = 0
for th in score_th:
    TP = 0
    P_sample = []
    for i in range(len(new_gt_label)):
        if float(new_gt_label[i][0]) > th:
            P_sample.append(new_gt_label[i])
    for i in range(len(P_sample)):
        if float(P_sample[i][1]) == 1.:
            TP +=1
    precision = TP/len(P_sample)

    T = 0
    for i in range(len(new_gt_label)):
        if float(new_gt_label[i][1]) == 1.:
            T +=1
    recall = TP/T
    pred.append(precision)
    rec.append(recall)
    print(TP, len(P_sample), T, precision, recall)
    AP += precision*0.02
print(AP*100)
plt.plot(rec, pred, 'r')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.show()

测试集中类别‘9’的P-R曲线如下图：

曲线下的面积就是类别‘9’的AP值，积分算得结果为73.07285589187525

2.6 各类别P-R曲线绘制及AP分析

所有类别的P-R曲线如图：

可以看出，模型对数字3、8、9检测性能较高，而对数字1、7、0的检测性能就比较低。

2.7 计算mAP

mAP，就是算出所有类别的AP值，取平均即为mAP。

# [类别， AP值]  按AP值由大到小
[[3, 100.0], 
[7, 99.79166666666667], 
[4, 98.8562091503268],
[5, 95.48391002936457], 
[9, 95.37272926643774], 
[8, 89.34690037631213], 
[6, 85.63968009952173], 
[0, 84.14080459770115], 
[2, 83.99250649250651], 
[1, 73.01194135976743]]

mAP: 90.56363480386048

文中若有理解不当之处，感谢指正。

3. 参考资料

1.https://blog.csdn.net/cdknight_happy/article/details/86553058
2.https://blog.csdn.net/willa_pudding/article/details/47056403
3.https://blog.csdn.net/u011956147/article/details/78967145