大话数据结构笔记(1)-线性表
目录
1.线性表的定义
2.线性表顺序存储结构
3.顺序存储结构的插入与删除
4.线性表顺序存储结构优缺点
5.线性表的链式存储结构
6.单链表的读取
7.单链表的插入与删除
8.单链表与顺序存储结构的优缺点
1.线性表的定义
线性表,从名字上就能了解到,是像线一样的性质的表。在广场上分散着很多人,有大人,小孩,宠物,大家都分散在各地,这样不能称之为线性表;但是像学校里面,大家在操场上做广播体操的时候,排着的单列纵队,有一个打头,一个收尾,中间的同学都知道他前面的是谁,后面的是谁,像一根线串联起来,这样就能称之为线性表。
线性表:零个或多个数据元素的有限序列。
这里需要强调几个关键的地方。
- 首先它是一个序列。也就是说,元素之间是顺序的,每个元素只能有一个前驱,一个后继。(第一个元素无前驱,最后一个元素无后继)
- 其次它是有限的,一个班级的人数是有限的,那种无限的数列,只存在与数学的概念中。
2.线性表顺序存储结构
2.1 顺序存储定义
线性表的顺序存储结构,指的是用一段地址连续的存储单元一次存储线性表的数据元素。
如图:
| a1 | a2 | ......... | a(i-1) | ai | ....... | an |
2.2 顺序存储方式
线性表的顺序存储结构,说白了,就是在内存中找一块地址连续的空间,然后把相同数据类型的元素依次存放到这块空间中。既然线性表的每个数据元素类型都相同,所以可以使用Java语言(其他语言也相同)的一维数组来实现,把第一个元素存放到数组下标为0的位置上,接着把其他元素存储在数组中相邻的位置上。
举个例子:
大学宿舍一共8个人,还有一个星期要期末考试了,大家都准备去图书馆学习学习,其中小王起的比较早,然后其他同学都让小王帮忙抢个座;小王到图书馆后,找了一排空座位,自己坐在第一个,然后拿书依次在自己右边占了七个座,宿舍其他人到了后,依次按序入座。这里的图书馆可以理解为内存,小王加上自己一个占了八个座,可以理解为在内存中申请了一块地址连续的,长度为八的空间,如果小王占少了,那么其他人自然坐不下了,如果占多了,那么座位就有剩余,相对的,也就造成内存空间一定的浪费。
来看看Java语言是怎么申请一个数组的。
/**
* 定义了一个长度为8的字符串数组,用于存放学生的名字
*/
String[] studentNames = new String[8];
2.3 地址计算方法
我们平时计数都是从1开始,不过在Java语言中,数组却是从0开始计数的,如果想要找第i个元素,则该元素在数组中的下标为i-1的位置,如图:
| 元素: | a1 | a2 | ....... | ai | a(i+1) | ...... | an |
| 下标 | 0 | 1 | ..... | i-1 | i | ...... | n-1 |
/**
* 表示获取小王的名字,小王坐在第一位,对应的下标为0
*/
String xiaoWang = studentNames[0];
/**
* 表示获取小赵的名字,小赵坐在最后一位,对应的下标为7
*/
String xiaoZhao = studentNames[7];另外,在计算机内存中,每块空间都会标注具体的地址,就像电影院中,每个座位都会有一个唯一的编号(x排y座),当我们拿着电影票进场后,根据5排3座,我们就能立刻找到自己的座位,而不用在电影院里面指着座位问服务员这个是不是5排3座,然后再指着另外一个座位问一遍,直到找到自己的座位。
所以当我们直接使用studengNames[0]的时候,计算机就能立刻找到存放学生的名字数组的存储空间,然后根据下标0取出存放在第一位的数据元素,使用studengNames[7]来获取最后一个数据元素的时候,耗时是一样的,因此我们得出结论,对于数组,我们获取其中任意一个元素的时间都是一样的,其时间复杂度为O(1)【常数阶】,而对于上面提到的需要每次都要询问一下座位是否是自己的场景,随着电影院里面的座位的增加,耗时也会增加,我们称其时间复杂度为O(n)【线性阶】。
3.顺序存储结构的插入与删除
3.1 插入操作
上面我们已经知道怎么从数组中获取元素了,下面我们来看下怎么往数组中插入元素。
/**
* 我们定义一个数组,用于存放食堂打饭排队的人名
*/
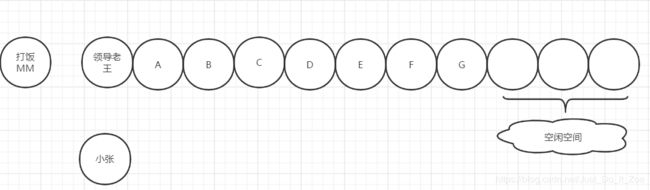
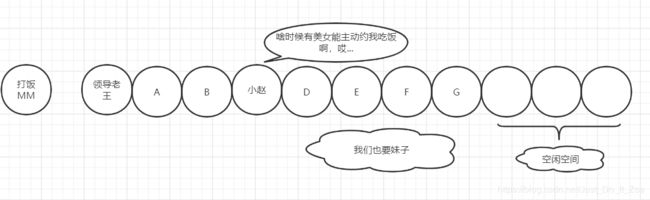
String[] rice = new String[100];举个例子,公司有自己的食堂,员工中午吃饭的时候就需要到食堂排队打饭,小张平时经常锻炼,所以体格又壮,跑的又快,今天中午小张凭借自身过硬的身体素质,意料之中排到了打饭队伍的第一位,正想着今天吃点啥的时候,旁边小张的领导老王慢慢的走了过来,老王今天有点忙,一会还有会议要开,看着这长长的队伍,眉头紧锁,想着只能买点面包对付下了,此时正好看到了大块头小张,顿时眉头舒展,走过去跟小张商量了下,“小张啊,我一会还有个重要的会议,来不及排队了,是否可以让我先打饭。”,小张虽然也很饿,不过领导有事相求,肯定得答应啊,于是小张把第一位给了老王。
如图:
插队前
插队后
这种情况,相当于直接把数组中排第一的元素“小张”替换为“领导老王”,此时数组长度不变,这里需要注意,这种操作属于元素替换,并不是元素插入,我们看一下使用java语言如何描述
/**
* 直接将数组中的第一个元素替换为“领导老王”
*/
rich[0] = "领导老王";此时饥肠辘辘的小张有三个选择
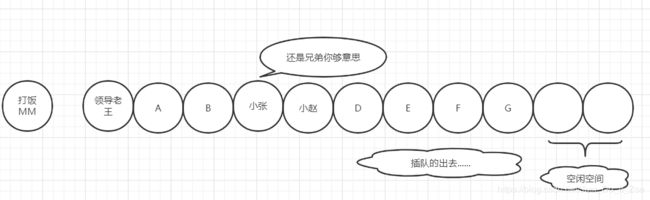
- 看能不能找到认识的同事插队
这次小张运气很好,一下就碰到了铁哥们小赵
插队后
使用Java语言实现
/** 队伍长度为8,下标对应0-7,因为要加一个人进来,所以下标要从8开始 */
for (int i = 8; i >= 3; i--) {
/** 从下标8开始,将前面以为元素往后移动一位,当到下标3,即原来小赵的位置结束 */
rice[i] = rice[i - 1];
}
/** 将小赵的位置,设置为小张 */
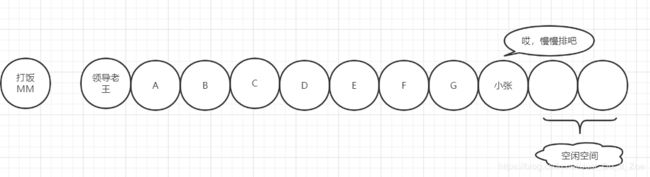
rice[3] = "小张";- 排到队伍最后面慢慢等
- 不等了,直接去外面买 面包吃
针对最后一种情况,相当于元素“小张”从数组中移除,而空下来的位置,正好被“领导老王”占用。
3.2 删除操作
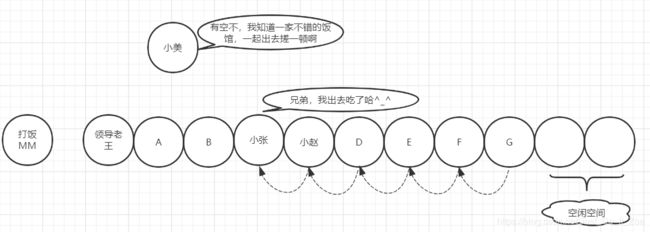
还是接着刚才的例子,话说小张终于插队成功,可是后面排队的人不干,大家都饿的很,怎么能这样随便插队呢,太没素质了,最终小张在舆论的压力下,准备离开队伍,此时逛了一圈发现没啥喜欢吃的小美正好看到了小张,小张这个人,平时为人实在,长的帅,因为经常锻炼身材保持的也不不错,所以小美对小张印象不错,正好灵机一动,就邀约小张一起出去吃午饭,对于小张自然是乐意的很,能跟美女一同共进午餐的机会可不是啥时候都有的,在同事羡慕的目光中,跟小美走出了食堂。
离开前
离开后
使用Java语言实现
/**
* 小张插队后的队伍长度为9,下标对应0-8,小张插队的下标为3,
* 所以从下标4开始,所有元素往前移动一位
*/
for (int i = 3; i <= 8; i++) {
/** 从小张的下标3开始,将后面的元素移动到自己的位置上 */
rice[i] = rice[i + 1];
}4.线性表顺序存储结构优缺点
优点
- 可以快速地获取表中任意位置的元素
缺点
- 插入和删除操作,需要涉及到大量的元素位移,耗时多
5.线性表的链式存储结构
5.1 顺序存储结构不足的解决办法
前面提到,顺序存储结构的缺点主要是在插入和删除的时候,需要移动大量元素,比较耗费时间。那么如何解决这个问题?
要解决这个问题,需要考虑以下几个问题,为什么插入删除时候需要移动元素?怎么才能不移动元素也能插入和删除?
针对第一个问题,我们发现,顺序存储结构初始化的时候,就在内存中申请了一块连续的空间,由于是连续的,所以在相邻的两个元素之间插入的时候,必须把后面的元素后移一位。
针对第二个问题,如果我们给两个元素之间预留足够的空间,能解决移动问题,但是会带来巨大的空间浪费,另外这个足够的空间到底要给多大也不好定义。所以我们换种思考模式,假设不需要连续的空间,当我们要把元素B插入相邻的AC两者之间时,我们在内存中任意找一个空闲的空间存放这个插入的元素B,然后我们只要解决当访问第二个元素的时候能知道怎么找到插入的B元素,而不是以前的C元素就能解决第二个问题。
5.2 链式存储结构定义
为了表示每个数据元素a(i)与其直接后继数据元素a(i+1)之间的关系,对于数据元素a(i)来说,除了存储自身的数据信息外,还需要存储一个指示其直接后继的信息(即直接后继在内存中的地址)。我们把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称作指针或链。这两部分信息组成数据元素a(i),称为节点(Node)。链表中的第一个Node称为头结点,头结点的数据域不存储数据,只有指针域中会存放链表第一个节点的地址。
从上述的定义中我们可以看到,使用链式存储结构就能解决移动元素的问题,因为每个Node中都会存放指向下一个Node的地址(通常叫指针,但是在Java语言中不再使用指针概念,因此我们称之为地址),所以我们只要通过遍历整个链表,就能找到任意的一个元素,大家注意遍历这个词,想想电影院不给座位标号,通过不断询问工作人员找座位的场景,所以链表的时间复杂度为O(n)【线性阶】,每次找元素都要从头开始遍历,随着链表的长度增加,耗时也会不断增加。
在Java语言中,每个节点的定义如下:
Node{
/** 存储具体的元素,T为定义存储元素的数据类型 **/
T element;
/** 存储前驱节点,如果是第一个节点,则前驱节点为空 **/
Node pre;
/** 存储后继节点,如果是最后一个节点,则后继节点为空 **/
Node next;
}6.单链表的读取
在顺序存储结构中,要获取某个位置的元素很容易,直接根据下标就能获取到。但是单链表中就没那么简单了,当我们要获取第i个节点的数据时,没办法一下子就知道,必须得从头节点开始,一个一个的往后遍历。
/** 初始化一个链表,链表中的存储的元素类型是字符串类型 **/
LinkedList students = new LinkedList<>(Arrays.asList("老王", "小刘", "小明", "老张"));
/** 在java语言中,所有的下标都是从0开始 **/
for (int i = 0; i < students.size(); i++) {
/** 从头节点开始遍历每个元素,如果元素是小刘,则输出元素所在的节点 **/
if (students.get(i).equals("小刘")) {
/** 这里最终输出 “小刘在下标为1的节点”,即第二个节点 **/
System.out.println(students.get(i) + "在下标为" + i + "的节点");
}
} 7.单链表的插入与删除
7.1 插入
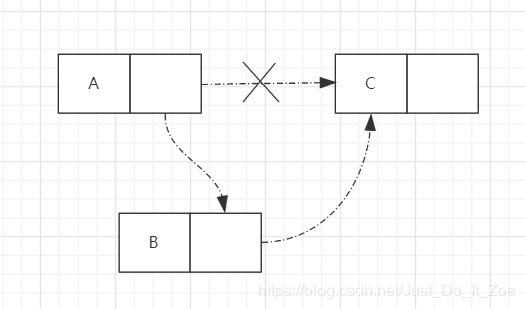
假设需要我们需要A,C两个节点之间,插入一个B节点,我们只需要将把A指向C节点的指针删除,然后重新指向B节点,同时再把B节点的下个节点指向C节点,如下图。
使用Java代码描述
LinkedList students = new LinkedList<>(Arrays.asList("A", "C"));
/** 在AC之间插入B,那插入的下标就是1 **/
students.add(1, "B"); Java语言已经对底层的各种操作做了封装,所以直接使用add方法就能实现把B插入AC之间,具体的底层实现逻辑如下
add(LinkedList list,int index,String element){
/** 获取要插入位置的节点,例子中的话就是节点C **/
Node originalNode = list.get(index);
/** 获取对应节点的前驱节点,例子中的节点A **/
Node preNode = originalNode.pre;
/** 创建一个要插入的节点B,element为B,前驱节点为A,后继节点为C **/
Node newNode = new Node(element,preNode,originalNode);
/** 把节点C的前驱节点设置为新创建的节点B **/
originalNode.pre = newNode;
/** 把以前后继节点指向C的A节点的后继节点重新指向新创建的B **/
preNode.next = newNode;
} 7.2 删除
现在我们来看删除,假设链表有A,B,C三个节点,需要删除B节点,那么我们只要把AB合BC直接的连接删除,然后直接把A指向C即可,如图
使用Java语言描述
LinkedList students = new LinkedList<>(Arrays.asList("A", "B", "C"));
/** 使用封装好的方法,直接删除下标为1的B元素 **/
students.remove(1); 具体的实现逻辑
remove(LinkedList list,int index){
/** 获取要删除的节点B,对应下标为1 **/
Node removeNode = list.get(index);
/** 获取节点B的前驱节点A **/
Node pre = removeNode.pre;
/** 获取节点B的后继节点C **/
Node next = removeNode.next;
/** 把A节点的后继节点直接指向C **/
pre.next = next;
/** 把C节点的前驱节点直接指向A **/
next.pre = pre;
}
8.单链表与顺序存储结构的优缺点
存储分配方式
- 顺序存储结构需要使用一段连续的物理地址来存储元素
- 链表使用链式存储结构,对物理地址的连续性没有要求,可以是内存中任意一块空闲地址
时间性能
- 顺序存储结构,查找为常数级O(1),链表为线性级O(n)
- 插入和删除,顺序存储结构需要涉及元素位移,时间为O(n),链表只需要修改节点的指向地址,不涉及元素位移,时间为O(1)
空间性能
- 顺序存储节点,需要提前分配合适的空间,大了浪费,小了容易溢出(超过申请的空间的长度)
- 单链表不需要,只有在每次插入元素的时候才会动态申请一块空间加入链表
结论:如果读取多,插入删除少,则使用顺序存储结构;如果插入删除多,读取少,则使用链式存储结构。