机器学习入门(python实现逻辑回归二分类)
文章目录
- 数据准备
- 文件数据转矩阵
- 数据初始化
- 逻辑回归函数
- 训练数据
- 测试
- 完整代码
数据准备
在前面一篇文章中已经为大家介绍了逻辑回归的原理,以及损失函数的推导,今天我们先来练练手,不借助任何机器学习库,用python实现逻辑回归的二分类。
这里数据是一份标准化后的男生女生身高体重的部分数据,最后一列是标签
data.txt
-0.017612 -14.053064 0.0
-1.395634 -4.662541 1.0
-0.752157 -6.53862 0.0
-1.322371 -7.152853 0.0
0.423363 -11.054677 0.0
0.406704 -7.067335 1.0
0.667394 -12.741452 0.0
-2.46015 -6.866805 1.0
0.569411 -9.548755 0.0
-0.026632 -10.427743 0.0
0.850433 -6.920334 1.0
1.347183 -13.1755 0.0
1.176813 -3.16702 1.0
-1.781871 -9.097953 0.0
-0.566606 -5.749003 1.0
0.931635 -1.589505 1.0
-0.024205 -6.151823 1.0
-0.036453 -2.690988 1.0
-0.196949 -0.444165 1.0
1.014459 -5.754399 1.0
1.985298 -3.230619 1.0
-1.693453 0.55754 1.0
-0.576525 -11.778922 0.0
-0.346811 1.67873 1.0
-2.124484 -2.672471 1.0
1.217916 -9.597015 0.0
-0.733928 -9.098687 0.0
-3.642001 1.618087 1.0
0.315985 -3.523953 1.0
1.416614 -9.619232 0.0
-0.386323 -3.989286 1.0
0.556921 -8.294984 1.0
1.224863 -11.58736 0.0
-1.347803 2.406051 1.0
1.196604 -4.951851 1.0
0.275221 -9.543647 0.0
0.470575 -9.332488 0.0
-1.889567 -9.542662 0.0
-1.527893 -12.150579 0.0
-1.185247 -11.309318 0.0
-0.445678 -3.297303 1.0
1.042222 -6.105155 1.0
-0.618787 -10.320986 0.0
1.152083 -0.548467 1.0
0.828534 -2.676045 1.0
-1.237728 -10.549033 0.0
-0.683565 2.166125 1.0
0.229456 -5.921938 1.0
-0.959885 -11.555336 0.0
0.492911 -10.993324 0.0
0.184992 -8.721488 0.0
-0.355715 -10.325976 0.0
-0.397822 -8.058397 0.0
0.824839 -13.730343 0.0
1.507278 -5.027866 1.0
0.099671 -6.835839 1.0
-0.344008 -10.717485 0.0
1.785928 -7.718645 1.0
-0.918801 -11.560217 0.0
-0.364009 -4.7473 1.0
-0.841722 -4.119083 1.0
0.490426 -1.960539 1.0
-0.007194 -9.075792 0.0
0.356107 -12.447863 0.0
0.342578 -12.281162 0.0
-0.810823 1.466018 1.0
2.530777 -6.476801 1.0
1.296683 -11.607559 0.0
0.475487 -12.040035 0.0
-0.783277 -11.009725 0.0
0.074798 -11.02365 0.0
-1.337472 -0.468339 1.0
-0.102781 -13.763651 0.0
-0.147324 -2.874846 1.0
0.518389 -9.887035 0.0
1.015399 -7.571882 0.0
-1.658086 0.027255 1.0
1.319944 -2.171228 1.0
2.056216 -5.019981 1.0
-0.851633 -4.375691 1.0
-1.510047 -6.061992 0.0
-1.076637 3.181888 1.0
1.821096 -10.28399 0.0
3.01015 -8.401766 1.0
-1.099458 -1.688274 1.0
-0.834872 1.733869 1.0
-0.846637 -3.849075 1.0
1.400102 -12.628781 0.0
1.752842 -5.468166 1.0
0.078557 -0.059736 1.0
0.089392 0.7153 1.0
1.825662 -12.693808 0.0
0.197445 -9.744638 0.0
0.126117 -0.922311 1.0
-0.679797 -1.22053 1.0
0.677983 -2.556666 1.0
0.761349 -10.693862 0.0
-2.168791 -0.143632 1.0
1.38861 6.341997 1.0
0.317029 10.739025 1.0
文件数据转矩阵
# 数据文件转矩阵
# delimiter: 文件分隔符
def file2matrix(self,delimiter):
with open(self.data,"r") as fp:
content = fp.read()
rowlist = content.splitlines() # 按行转换为一维表
# 逐行遍历
# 结果按分隔符分割为行向量
recordlist = [row.split(delimiter) for row in rowlist if row.strip()]
return mat(recordlist).astype(float) # 返回转换后的矩阵形式
可能有人会对最后一行代码不理解,这里我解释一下,因为文件读取时候是以字符串的格式讲数据存在列表里,而后面这些数据要用于计算,需要转换成数据格式,而astype()是numpy库中的方法,他可以转换数组的数据类型,而后面的float是python的内置类型,但是numpy是可以使用的,会将python类型映射到等价的dtype上。
数据初始化
def initdata(self,matdata):
target = matdata[:, -1] # 获取分类标签列表
[m, n] = shape(matdata)
weights = ones((n, 1)) # 初始化权重向量
dataMat = self.buildMat(matdata) # 构建x+b 系数矩阵:b这里默认为1
return target,weights,dataMat#返回标签列表,初始化权重,系数矩阵
在训练过程中我们需要拿到数据的标签,对权重给个初始化值,这里我们都将其设置为1。强调一下我们这里权重是三个,身高,体重,以及偏置b。
另外,在前面的文章中,大家应该记得
f ( x i , w , , b ) = [ x i 1 . . . x i j ] [ w 1 ⋮ w j ] + b = [ x i 1 . . . x i j 1 ] [ w 1 ⋮ w j b ] = w i ~ x i ~ f(x_i,w,,b) = [x_{i1} ...x_{ij}]\begin{bmatrix} w_1 \\ \vdots\\ w_j \end{bmatrix}+b=[x_{i1} ...x_{ij} \space\space1]\begin{bmatrix} w_1 \\ \vdots\\ w_j\\ b \end{bmatrix}=\widetilde{w_i}\widetilde{x_i} f(xi,w,,b)=[xi1...xij]⎣⎢⎡w1⋮wj⎦⎥⎤+b=[xi1...xij 1]⎣⎢⎢⎢⎡w1⋮wjb⎦⎥⎥⎥⎤=wi xi
这个公式的变化吧
dataMat[:, 0] = 1
dataMat[:, 1:] = dataSet[:, :-1] # 取原始数据前两列
这两行代码上述公式的变化的实现,现在相信已经明白为什么要这样处理数据了吧
逻辑回归函数
# Logistic函数
def logistic(self,wx):
return 1.0 / (1.0 + exp(-wx))
这个就是我们前面所说的sigmod函数。这里我就不多说了
训练数据
下面就进入到我们的重头戏了,先附上代码为敬
def train(self,dataMat, target,weights):
for k in range(self.steps):
# wx
gradient = dataMat * mat(weights)
# sigmoid(wx)
output = self.logistic(gradient) # logistic function
errors = target - output # 计算误差
weights = weights + self.alpha * dataMat.T * errors
return weights
dataMat就是我们训练数据矩阵X,mat(weights)就是已经初始化为1的三个权重,然后拿真实的结果和通过逻辑回归预测的结果做误差分析,进而得到一个新的权重.
weights = weights + self.alpha * dataMat.T * errors
∇ L ( w ) = ∑ i ( y i − η ( w x i ) ) ∗ x i \nabla L(w)=\sum_i(y_i-\eta(wx_i))*x_i ∇L(w)=i∑(yi−η(wxi))∗xi
这行代码就是前面我们推导出来的损失函数的一个实现
现在我们先来看一下结果
logic = Logistic("data.txt",alpha = 0.001,steps=500)
input = logic.file2matrix("\t")
target, weights, dataMat=logic.initdata(input)
#print(target,weights,dataMat)
logic.drawScatterbyLabel(plt,input)
weight = logic.train(dataMat, target,weights)
print(weight)
#ouput
[[4.17881308]
[0.50489874]
[0.61980264]]
得到三个权重的值,这个就是我们训练的结果,也可以称之为模型
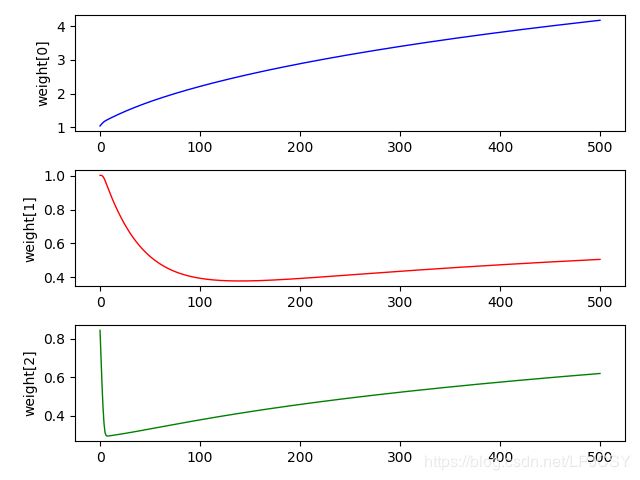
我们再来看一下这三个权重的变化曲线,我们在train()函数代码最后一行添加一行代码
weightlist.append(weight)
把每次迭代的权重都存在列表里
fig = plt.figure()
axes1 = plt.subplot(311)
axes2 = plt.subplot(312)
axes3 = plt.subplot(313)
weightmat = mat(zeros((steps,n)))
i=0
for weight in weightlist:
weightmat[i,:]=weight.T
i+= 1
X =linspace(0,steps,steps)
axes1.plot(X,weightmat[:,0],color = 'blue', linewidth=1, linestyle="-")
axes1.set_ylabel('weight[0]')
axes2.plot(X,weightmat[:,1],color = 'red', linewidth=1, linestyle="-")
axes2.set_ylabel('weight[1]')
axes3.plot(X,weightmat[:,2],color = 'green', linewidth=1, linestyle="-")
axes3.set_ylabel('weight[2]')
plt.show()
测试
上面我们得到的权重就可以看作是算法的模型,接下来我们就用训练出来模型来预测一下数据,首先来看一下分类函数
# 分类函数
def classifier(self,testData, weights):
prob = self.logistic(sum(testData * weights))
print(prob)
if prob > 0.5:
return 1.0 # prob>0.5 返回为1
else:
return 0.0 # prob<=0.5 返回为0
这里的prob就是我们设置的一个阈值,这个阈值是人工自己设置的,阈值设置的改变可能会改变算法模型的效果,所以一般情况下需要根据自己需求多次的测试才能找到一个合适的阈值
现在我们从前面的数据中找一组来试一下
#-1.237728 -10.549033 0.0
testdata = logic.buildMat(mat([-1.237728, -10.549033, 0.0]))
print(logic.classifier(testdata, weight))
#output
0.048134123711533014 0.0
#-0.851633 -4.375691 1.0
testdata = logic.buildMat(mat([-0.851633, -4.375691, 1.0]))
print(logic.classifier(testdata, weight))
#output
0.7382243224119601 1.0
我们再试一下把分类函数里面的阈值设置为0.8,再用上面两组数据做预测,然后分类结果就都是0.0,阈值的作用在这里就可以体现出来了,可以人工干预分类结果
这里强调一下,工作中我们的数据是有三部分,训练数据,测试数据,验证数据,原则上是不能拿训练数据做测试的
完整代码
import matplotlib.pyplot as plt
from numpy import *
class Logistic():
def __init__(self,datafile,alpha,steps):
self.data = datafile
self.alpha = alpha
self.steps = steps
# 数据文件转矩阵
# delimiter: 文件分隔符
def file2matrix(self,delimiter):
with open(self.data,"r") as fp:
content = fp.read()
rowlist = content.splitlines() # 按行转换为一维表
# 逐行遍历
# 结果按分隔符分割为行向量
recordlist = [row.split(delimiter) for row in rowlist if row.strip()]
return mat(recordlist).astype(float) # 返回转换后的矩阵形式
def initdata(self,matdata):
target = matdata[:, -1] # 获取分类标签列表
[m, n] = shape(matdata)
weights = ones((n, 1)) # 初始化权重向量
dataMat = self.buildMat(matdata) # 构建x+b 系数矩阵:b这里默认为1
return target,weights,dataMat#返回标签列表,初始化权重,系数矩阵
# Logistic函数
def logistic(self,wx):
return 1.0 / (1.0 + exp(-wx))
# 取身高和体重数据
def buildMat(self,dataSet):
m, n = shape(dataSet)
dataMat = zeros((m, n))
dataMat[:, 0] = 1
dataMat[:, 1:] = dataSet[:, :-1] # 取原始数据前两列
return dataMat
# 绘制分类点
def drawScatterbyLabel(self,plt, Input):
m, n = shape(Input)
target = Input[:, -1]
for i in range(m):
if target[i] == 0.0:
plt.scatter(Input[i, 0], Input[i, 1], c='blue', marker='o')
else:
plt.scatter(Input[i, 0], Input[i, 1], c='red', marker='s')
def train(self,dataMat, target,weights):
for k in range(self.steps):
# wx
gradient = dataMat * mat(weights)
# sigmoid(wx)
output = self.logistic(gradient) # logistic function
errors = target - output # 计算误差
weights = weights + self.alpha * dataMat.T * errors
return weights
# 分类函数
def classifier(self,testData, weights):
prob = self.logistic(sum(testData * weights))
print(prob)
if prob > 0.8:
return 1.0 # prob>0.5 返回为1
else:
return 0.0 # prob<=0.5 返回为0
if __name__=="__main__":
logic = Logistic("data.txt",alpha = 0.001,steps=500)
input = logic.file2matrix("\t")
target, weights, dataMat=logic.initdata(input)
#print(target,weights,dataMat)
logic.drawScatterbyLabel(plt,input)
weightmat = logic.train(dataMat, target,weights)
# print(weight)
testdata = logic.buildMat(mat([-1.237728, -10.549033, 0.0]))
print(logic.classifier(testdata, weightmat))
testdata = logic.buildMat(mat([-0.851633, -4.375691, 1.0]))
print(logic.classifier(testdata, weightmat))
```