一文理解Ranking Loss/Contrastive Loss/Margin Loss/Triplet Loss/Hinge Loss

一文理解Ranking Loss/Contrastive Loss/Margin Loss/Triplet Loss/Hinge Loss

翻译自FesianXu， 2020/1/13, 原文链接 https://gombru.github.io/2019/04/03/ranking_loss/

前言

ranking loss在很多不同的领域，任务和神经网络结构（比如siamese net或者Triplet net）中被广泛地应用。其广泛应用但缺乏对其命名标准化导致了其拥有很多其他别名，比如对比损失Contrastive loss，边缘损失Margin loss，铰链损失hinge loss和我们常见的三元组损失Triplet loss等。

本文翻译自https://gombru.github.io/2019/04/03/ranking_loss/，如有谬误，请提出指正，谢谢。

ranking loss函数：度量学习

不像其他损失函数，比如交叉熵损失和均方差损失函数，这些损失的设计目的就是学习如何去直接地预测标签，或者回归出一个值，又或者是在给定输入的情况下预测出一组值，这是在传统的分类任务和回归任务中常用的。ranking loss的目的是去预测输入样本之间的相对距离。这个任务经常也被称之为度量学习(metric learning)。

在训练集上使用ranking loss函数是非常灵活的，我们只需要一个可以衡量数据点之间的相似度度量就可以使用这个损失函数了。这个度量可以是二值的（相似/不相似）。比如，在一个人脸验证数据集上，我们可以度量某个两张脸是否属于同一个人（相似）或者不属于同一个人（不相似）。通过使用ranking loss函数，我们可以训练一个CNN网络去对这两张脸是否属于同一个人进行推断。（当然，这个度量也可以是连续的，比如余弦相似度。）

在使用ranking loss的过程中，我们首先从这两张（或者三张，见下文）输入数据中提取出特征，并且得到其各自的嵌入表达(embedded representation，译者：见[1]中关于数据嵌入的理解)。然后，我们定义一个距离度量函数用以度量这些表达之间的相似度，比如说欧式距离。最终，我们训练这个特征提取器，以对于特定的样本对（sample pair）产生特定的相似度度量。

尽管我们并不需要关心这些表达的具体值是多少，只需要关心样本之间的距离是否足够接近或者足够远离，但是这种训练方法已经被证明是可以在不同的任务中都产生出足够强大的表征的。

ranking loss的表达式

正如我们一开始所说的，ranking loss有着很多不同的别名，但是他们的表达式却是在众多设置或者场景中都是相同的并且是简单的。我们主要针对以下两种不同的设置，进行两种类型的ranking loss的辨析

1. 使用一对的训练数据点（即是两个一组）
2. 使用三元组的训练数据点（即是三个数据点一组）

这两种设置都是在训练数据样本中进行距离度量比较。

成对样本的ranking loss

Fig 2.1 成对样本ranking loss用以训练人脸认证的例子。在这个设置中，CNN的权重值是共享的。我们称之为Siamese Net。成对样本ranking loss还可以在其他设置或者其他网络中使用。

在这个设置中，由训练样本中采样到的正样本和负样本组成的两种样本对作为训练输入使用。正样本对$(x_a,x_p)$由两部分组成，一个锚点样本$x_a$ 和 另一个和之标签相同的样本$x_p$ ，这个样本$x_p$与锚点样本在我们需要评价的度量指标上应该是相似的（经常体现在标签一样）；负样本对$(x_a,x_n)$由一个锚点样本$x_a$和一个标签不同的样本$x_n$组成，$x_n$在度量上应该和$x_a$不同。（体现在标签不一致）

现在，我们的目标就是学习出一个特征表征，这个表征使得正样本对中的度量距离$d$尽可能的小，而在负样本对中，这个距离应该要大于一个人为设定的超参数——阈值$m$。成对样本的ranking loss强制样本的表征在正样本对中拥有趋向于0的度量距离，而在负样本对中，这个距离则至少大于一个阈值。用$r_a,r_p,r_n$分别表示这些样本的特征表征，我们可以有以下的式子：
$$L=\{\begin{array}{ll}\mathrm{d}(r_a,r_p)& 正样本对(x_a,x_p)\\ \max (0,m-\mathrm{d}(r_a,r_n))& 负样本对(x_a,x_n)\end{array}\text{\hspace{1em}(2.1)}$$
对于正样本对来说，这个loss随着样本对输入到网络生成的表征之间的距离的减小而减少，增大而增大，直至变成0为止。

对于负样本来说，这个loss只有在所有负样本对的元素之间的表征的距离都大于阈值$m$的时候才能变成0。当实际负样本对的距离小于阈值的时候，这个loss就是个正值，因此网络的参数能够继续更新优化，以便产生更适合的表征。这个项的loss最大值不会超过$m$，在$\mathrm{d}(r_a,r_n)=0$的时候取得。这里设置阈值的目的是，当某个负样本对中的表征足够好，体现在其距离足够远的时候，就没有必要在该负样本对中浪费时间去增大这个距离了，因此进一步的训练将会关注在其他更加难分别的样本对中。

假设用$r_0,r_1$分别表示样本对两个元素的表征，$y$是一个二值的数值，在输入的是负样本对时为0，正样本对时为1，距离$d$是欧式距离，我们就能有最终的loss函数表达式：
$$L(r_0,r_1,y)=y||r_0-r_1||+(1-y)\max (0,m-||r_0-r_1||)\text{\hspace{1em}(2.2)}$$

三元组样本对的ranking loss

三元组样本对的ranking loss称之为triplet loss。在这个设置中，与二元组不同的是，输入样本对是一个从训练集中采样得到的三元组。这个三元组$(x_a,x_p,x_n)$由一个锚点样本$x_a$，一个正样本$x_p$，一个负样本$x_n$组成。其目标是锚点样本与负样本之间的距离$\mathrm{d}(r_a,r_n)$ 与锚点样本和正样本之间的距离$\mathrm{d}(r_a,r_p)$之差大于一个阈值$m$，可以表示为：
$$L(r_a,r_p,r_n)=\max (0,m+\mathrm{d}(r_a,r_p)-\mathrm{d}(r_a,r_n))\text{\hspace{1em}(2.3)}$$

Fig 2.2 Triplet loss的例子，其中的CNN网络的参数是共享的。

在训练过程中，对于一个可能的三元组，我们的triplet loss可能有三种情况：

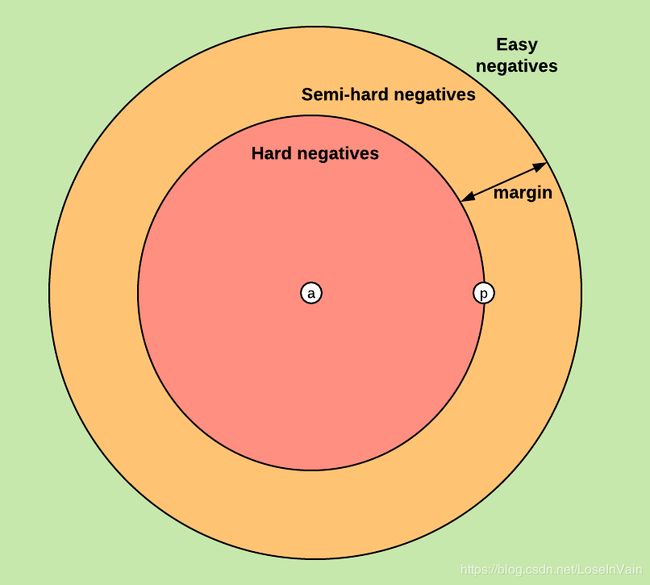
• “简单样本”的三元组(easy triplet)：$\mathrm{d}(r_a,r_n)>\mathrm{d}(r_a,r_p)+m$。在这种情况中，在嵌入空间（译者：指的是以嵌入特征作为表征的欧几里德空间，空间的每个基底都是一个特征维，一般是赋范空间）中，对比起正样本来说，负样本和锚点样本已经有足够的距离了（即是大于$m$）。此时loss为0，网络参数将不会继续更新。
• “难样本”的三元组(hard triplet)：$\mathrm{d}(r_a,r_n)<\mathrm{d}(r_a,r_p)$。在这种情况中，负样本比起正样本，更接近锚点样本，此时loss为正值（并且比$m$大），网络可以继续更新。
• “半难样本”的三元组(semi-hard triplet)：$\mathrm{d}(r_a,r_p)<\mathrm{d}(r_a,r_n)<\mathrm{d}(r_a,r_p)+m$。在这种情况下，负样本到锚点样本的距离比起正样本来说，虽然是大于后者，但是并没有大于设定的阈值$m$，此时loss仍然为正值，但是小于$m$，此时网络可以继续更新。

Fig 2.3 三元组可能的情况。

负样本的挑选

在训练中使用Triplet loss的一个重要选择就是我们需要对负样本进行挑选，称之为负样本选择（negative selection）或者三元组采集（triplet mining）。选择的策略会对训练效率和最终性能结果有着重要的影响。一个明显的策略就是：简单的三元组应该尽可能被避免采样到，因为其loss为0，对优化并没有任何帮助。

第一个可供选择的策略是离线三元组采集（offline triplet mining），这意味着在训练的一开始或者是在每个世代（epoch）之前，就得对每个三元组进行定义（也即是采样）。第二种策略是在线三元组采集（online triplet mining），这种方案意味着在训练中的每个批次（batch）中，都得对三元组进行动态地采样，这种方法经常具有更高的效率和更好的表现。

然而，最佳的负样本采集方案是高度依赖于任务特性的。但是在本篇文中不会在此深入讨论，因为本文只是对ranking loss的不同别名的综述并且讨论而已。可以参考[2]以对负样本采样进行更深的了解。

ranking loss的别名们~名儿可真多啊

ranking loss家族正如以上介绍的，在不同的应用中都有广泛应用，然而其表达式都是大同小异的，虽然他们在不同的工作中名儿并不一致，这可真让人头疼。在这里，我尝试对为什么采用不同的别名，进行解释：

• ranking loss：这个名字来自于信息检索领域，在这个应用中，我们期望训练一个模型对项目（items）进行特定的排序。比如文件检索中，对某个检索项目的排序等。
• Margin loss：这个名字来自于一个事实——我们介绍的这些loss都使用了边界去比较衡量样本之间的嵌入表征距离，见Fig 2.3
• Contrastive loss：我们介绍的loss都是在计算类别不同的两个（或者多个）数据点的特征嵌入表征。这个名字经常在成对样本的ranking loss中使用。但是我从没有在以三元组为基础的工作中使用这个术语去进行表达。
• Triplet loss：这个是在三元组采样被使用的时候，经常被使用的名字。
• Hinge loss：也被称之为max-margin objective。通常在分类任务中训练SVM的时候使用。他有着和SVM目标相似的表达式和目的：都是一直优化直到到达预定的边界为止。

Siamese 网络和 Triplet网络

Siamese网络（Siamese Net）和Triplet网络（Triplet Net）分别是在成对样本和三元组样本 ranking loss采用的情况下训练模型。

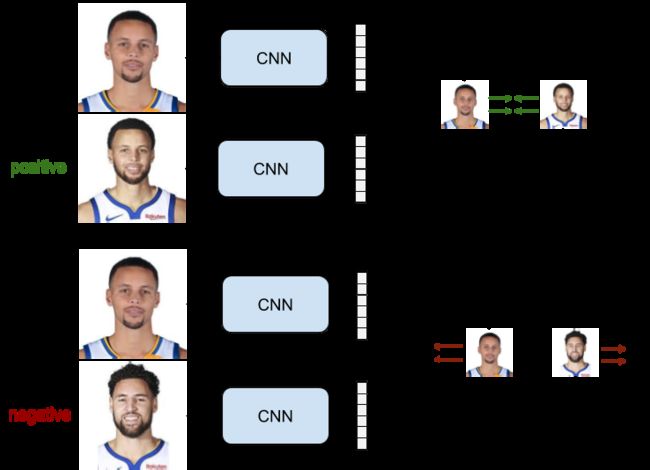
Siamese网络

这个网络由两个相同并且共享参数的CNN网络（两个网络都有相同的参数）组成。这些网络中的每一个都处理着一个图像并且产生对于的特征表达。这两个表达之间会进行比较，并且计算他们之间的距离。然后，一个成对样本的ranking loss将会作为损失函数进行训练模型。

我们用$f(x)$表示这个CNN网络，我们有Siamese网络的损失函数如：
$$L(x_0,x_1,y)=y||f(x_0)-f(x_1)||+(1-y)\max (0,m-||f(x_0)-f(x_1)||)\text{\hspace{1em}(4.1)}$$

Triplet网络

这个基本上和Siamese网络的思想相似，但是损失函数采用了Triplet loss，因此整个网络有三个分支，每个分支都是一个相同的，并且共享参数的CNN网络。同样的，我们能有Triplet网络的损失函数表达为：
$$L(x_a,x_p,x_n)=\max (0,m+||f(x_a)-f(x_p)||-||f(x_a)-f(x_n)||)\text{\hspace{1em}(4.2)}$$

在多模态检索中使用ranking loss

根据我的研究，在涉及到图片和文本的多模态检索任务中，使用了Triplet ranking loss。训练数据由若干有着相应文本标注的图片组成。任务目的是学习出一个特征空间，模型尝试将图片特征和相对应的文本特征都嵌入到这个特征空间中，使得可以将彼此的特征用于在跨模态检索任务中（举个例子，检索任务可以是给定了图片，去检索出相对应的文字描述，那么既然在这个特征空间里面文本和图片的特征都是相近的，体现在距离近上，那么就可以直接将图片特征作为文本特征啦~当然实际情况没有那么简单）。为了实现这个，我们首先从孤立的文本语料库中，学习到文本嵌入信息（word embeddings），可以使用如同Word2Vec或者GloVe之类的算法实现。随后，我们针对性地训练一个CNN网络，用于在与文本信息的同一个特征空间中，嵌入图片特征信息。

具体来说，实现这个的第一种方法可以是：使用交叉熵损失，训练一个CNN去直接从图片中预测其对应的文本嵌入。结果还不错，但是使用Triplet ranking loss能有更好的结果。

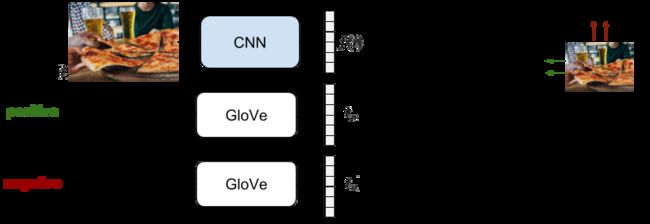
使用Triplet ranking loss的设置如下：我们使用已经学习好了文本嵌入（比如GloVe模型），我们只是需要学习出图片表达。因此锚点样本$a$是一个图片，正样本$p$是一个图片对应的文本嵌入，负样本$n$是其他无关图片样本的对应的文本嵌入。为了选择文本嵌入的负样本，我们探索了不同的在线负样本采集策略。在多模态检索这个问题上使用三元组样本采集而不是成对样本采集，显得更加合乎情理，因为我们可以不建立显式的类别区分（比如没有label信息）就可以达到目的。在给定了不同的图片后，我们可能会有需要简单三元组样本，但是我们必须留意与难样本的采样，因为采集到的难负样本有可能对于当前的锚点样本，也是成立的（虽然标签的确不同，但是可能很相似。）

在该实验设置中，我们只训练了图像特征表征。对于第$i$个图片样本，我们用$f(i)$表示这个CNN网络提取出的图像表征，然后用$t_p,t_n$分别表示正文本样本和负文本样本的GloVe嵌入特征表达，我们有：
$$L(i,t_p,t_n)=\max (0,m+||f(i)-t_p||-||f(i)-t_n||)\text{\hspace{1em}(5.1)}$$
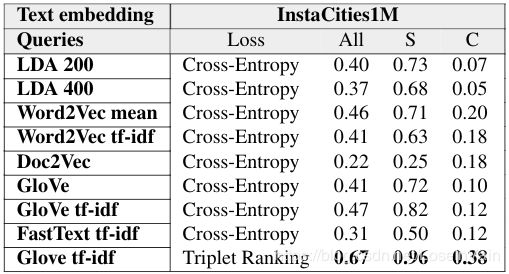
在这种实验设置下，我们对比了triplet ranking loss和交叉熵损失的一些实验的量化结果。我不打算在此对实验细节写过多的笔墨，其实验细节设置和[4,5]一样。基本来说，我们对文本输入进行了一定的查询，输出是对应的图像。当我们在社交网络数据上进行半监督学习的时候，我们对通过文本检索得到的图片进行某种形式的评估。采用了Triplet ranking loss的结果远比采用交叉熵损失的结果好。

深度学习框架中的ranking loss层

Caffe

• Constrastive loss layer
• pycaffe triplet ranking loss layer

PyTorch

• CosineEmbeddingLoss
• MarginRankingLoss
• TripletMarginLoss

TensorFlow

• contrastive_loss
• triplet_semihard_loss

Reference

[1]. https://blog.csdn.net/LoseInVain/article/details/88373506

[2]. https://omoindrot.github.io/triplet-loss

[3]. https://github.com/adambielski/siamese-triplet

[4]. https://arxiv.org/abs/1901.02004

[5]. https://gombru.github.io/2018/08/01/learning_from_web_data/