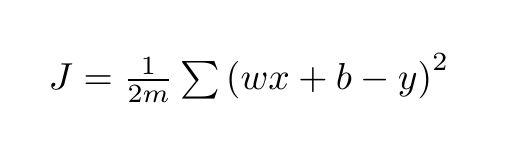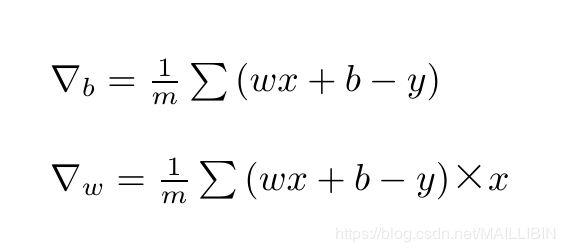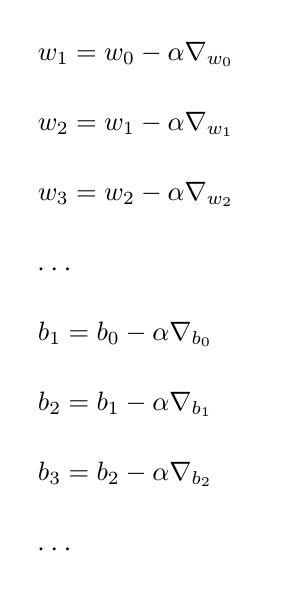梯度下降法实例

import numpy as np
import matplotlib.pyplot as plt
import random

#数据个数
M=10

#用于学习的数据x
x=np.array(range(10))

y0=np.random.rand(10)*5
y1=np.array(range(10,59,5))

#用于学习的数据y
y=y0+y1

#学习率
LEARNING_RATE = 0.01
w = 0
b = 0

#假定拟合函数:y=b+wx
def hypothesis(x):
    global b,w
    return b + w * x

#学习过程
def learn(x,y,alpha):
    global b,w
    bSum=0
    wSum=0
    
	#分别计算b和w的梯度
    for i in range(M):
        bSum+=(hypothesis(x[i])-y[i])
        wSum+=(hypothesis(x[i])-y[i])*x[i]
		
    #利用梯度下降寻找到最拟合的b和w值
    b=b-(alpha/M)*bSum
    w=w-(alpha/M)*wSum

#学习迭代次数
MAX_ITER=10000

for i in range(MAX_ITER):
    learn(x,y,LEARNING_RATE)
    print(i,"b:",b,"w:",w)

#绘图可视化学习的效果
y_learned=b+w*x

plt.scatter(x,y,color="red")
plt.plot(x,y_learned)
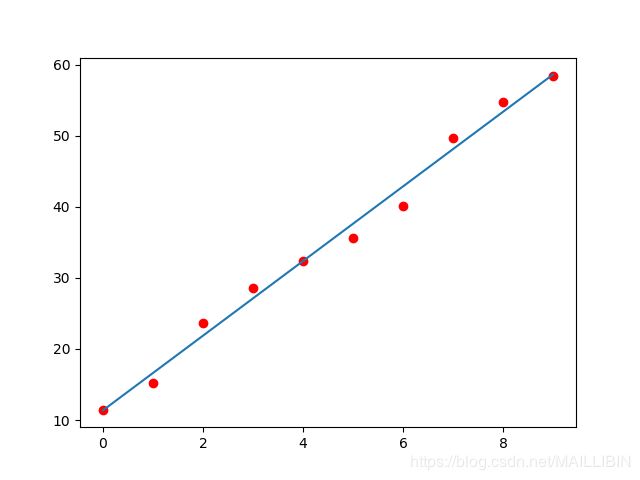
plt.show()

此例中数据拟合的效果如图：

红色的是开始观测到的数据，蓝色直线是通过数据学习后生成的拟合函数。

 

相关公式

 

梯度下降的目标就是求解出使以下方差最小的w和b值

 上述函数中的w和b的梯度其实就是对w和b进行求导

 初始设定一个随机的w和b值，然后以梯度乘以学习率的步长逐步迭代求得期望的w和b值