红黑树的插入和删除
本文转载于:https://blog.csdn.net/v_JULY_v/article/details/6105630
1、红黑树介绍
(1)二叉查找树
二叉查找树,也称有序二叉树(ordered binary tree),或已排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树。
- 没有键值相等的节点(no duplicate nodes)。
因为一棵由n个结点随机构造的二叉查找树的高度为lgn,所以顺理成章,二叉查找树的一般操作的执行时间为O(lgn)。但二叉查找树若退化成了一棵具有n个结点的线性链后,则这些操作最坏情况运行时间为O(n)。
(2)红黑树
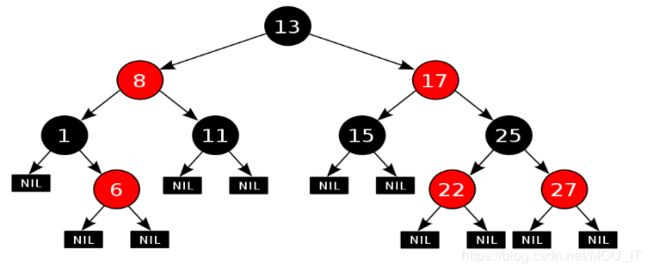
红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。但它是如何保证一棵n个结点的红黑树的高度始终保持在logn的呢?这就引出了红黑树的5个性质:
- 每个结点要么是红的要么是黑的。
- 根结点是黑的。
- 每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。
- 如果一个结点是红的,那么它的两个儿子都是黑的。
- 对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。
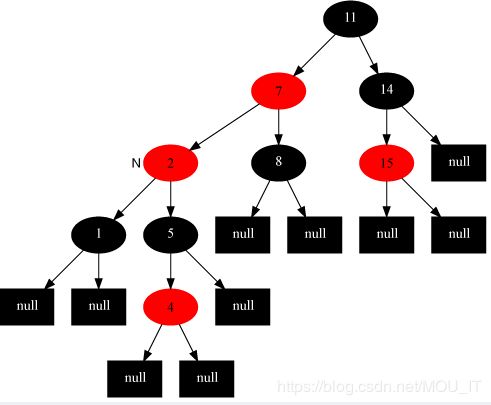
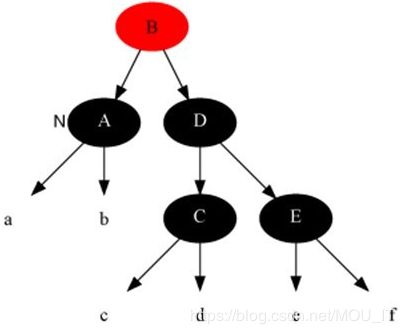
正是红黑树的这5条性质,对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。使一棵n个结点的红黑树始终保持了logn的高度,从而也就解释了上面所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)”这一结论成立的原因。如下图为一颗红黑树:
2、红黑树的插入
红黑树的插入节点总是设为红节点,当在对红黑树进行插入和删除等操作时,对树做了修改可能会破坏红黑树的性质。为了继续保持红黑树的性质,可以通过对结点进行重新着色,以及对树进行相关的旋转操作,即通过修改树中某些结点的颜色及指针结构,来达到对红黑树进行插入或删除结点等操作后继续保持它的性质或平衡的目的。
(1)如果插入的是根结点,由于原树是空树,此情况只会违反性质2,因此直接把此结点涂为黑色;
(2)如果插入的结点的父结点是黑色,由于此不会违反性质2和性质4,红黑树没有被破坏,所以此时什么也不做;
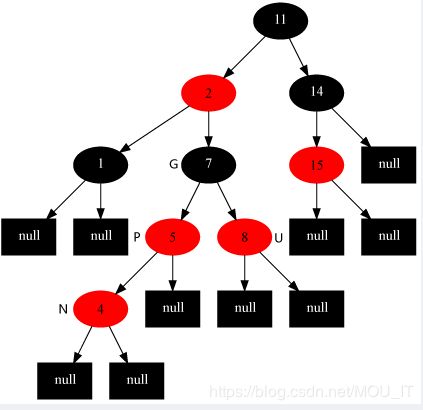
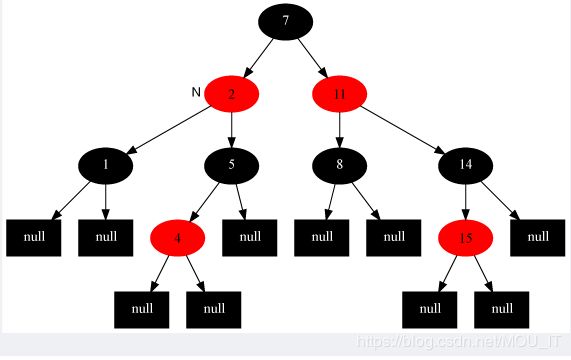
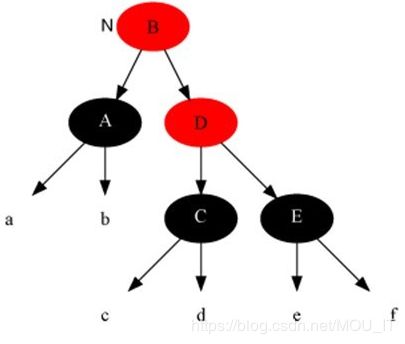
(3)插入修复情况1:如果当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色:
此时父结点的父结点一定存在,否则插入前就已不是红黑树。与此同时,又分为父结点是祖父结点的左孩子还是右孩子,根据对称性,我们只要解开一个方向就可以了。这里只考虑父结点为祖父左孩子的情况,如下图所示(勘误:图中15节点应改为13,特此说明,下同)。 对此,我们的解决策略是:将当前节点的父节点和叔叔节点涂黑,祖父结点涂红,把当前结点指向祖父节点,从新的当前节点重新开始算法。
于是,插入修复情况1转换成了插入修复情况2。
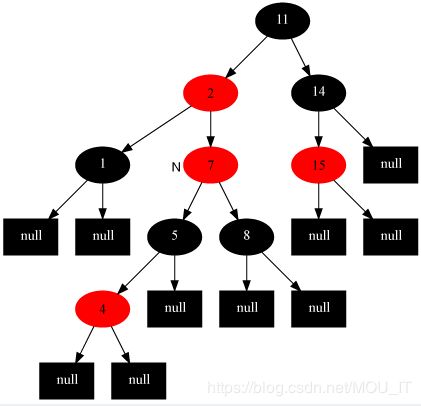
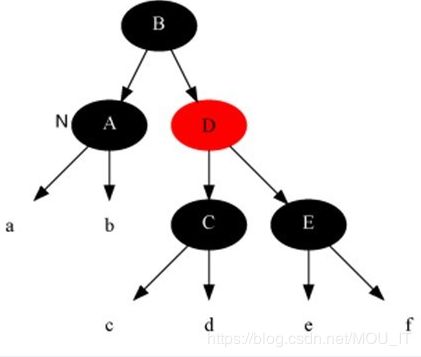
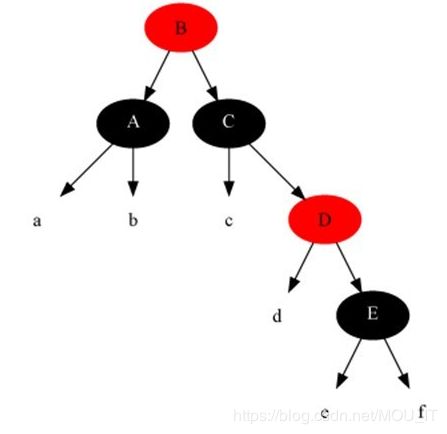
(4)插入修复情况2:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子:
此时,解决对策是:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
从而插入修复情况2转换成了插入修复情况3。
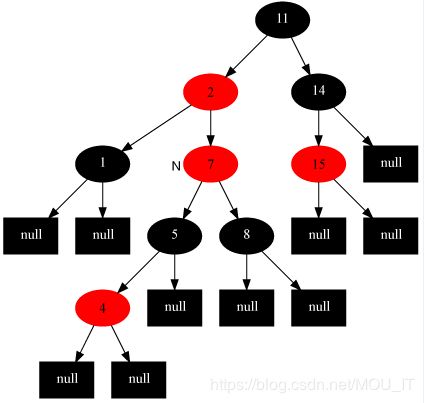
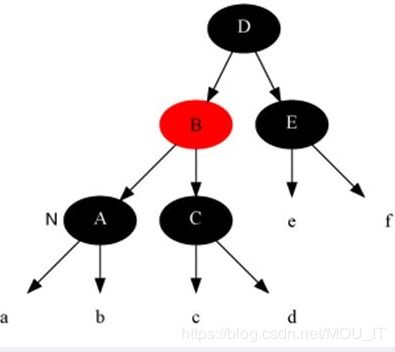
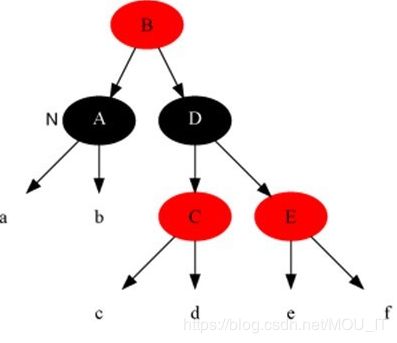
(5)插入修复情况3:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子:
解决对策是:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋,最后,把根结点涂为黑色,整棵红黑树便重新恢复了平衡。
3、红黑树的删除
在删除节点后,原红黑树的性质可能被改变,如果删除的是红色节点,那么原红黑树的性质依旧保持,此时不用做修正操作,如果删除的节点是黑色节点,原红黑树的性质可能会被改变,我们要对其做修正操作。那么哪些树的性质会发生变化呢,如果删除节点不是树唯一节点,那么删除节点的那一个支的到各叶节点的黑色节点数会发生变化,此时性质5被破坏。如果被删节点的唯一非空子节点是红色,而被删节点的父节点也是红色,那么性质4被破坏。如果被删节点是根节点,而它的唯一非空子节点是红色,则删除后新根节点将变成红色,违背性质2。
我们从被删节点后来顶替它的那个节点开始调整,并认为它有额外的一重黑色。这里额外一重黑色是什么意思呢,我们不是把红黑树的节点加上除红与黑的另一种颜色,这里只是一种假设,我们认为我们当前指向它,因此空有额外一种黑色,可以认为它的黑色是从它的父节点被删除后继承给它的,它现在可以容纳两种颜色,如果它原来是红色,那么现在是红+黑,如果原来是黑色,那么它现在的颜色是黑+黑。有了这重额外的黑色,原红黑树性质5就能保持不变。现在只要恢复其它性质就可以了,做法还是尽量向根移动和穷举所有可能性。
(1)当前节点是红+黑色,解法:直接把当前节点染成黑色,结束,此时红黑树性质全部恢复;
(2)当前节点是黑+黑且是根节点, 解法:什么都不做,结束;
(3)删除修复情况1:当前节点是黑+黑且兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑):
解法:把父节点染成红色,把兄弟结点染成黑色,之后重新进入算法(我们只讨论当前节点是其父节点左孩子时的情况)。此变换后原红黑树性质5不变,而把问题转化为兄弟节点为黑色的情况(注:变化前,原本就未违反性质5,只是为了把问题转化为兄弟节点为黑色的情况)。
(4)删除修复情况2:当前节点是黑加黑且兄弟是黑色且兄弟节点的两个子节点全为黑色:
解法:把当前节点和兄弟节点中抽取一重黑色追加到父节点上,把父节点当成新的当前节点,重新进入算法。(此变换后性质5不变):
(5)删除修复情况3:当前节点颜色是黑+黑,兄弟节点是黑色,兄弟的左子是红色,右子是黑色:
解法:把兄弟结点染红,兄弟左子节点染黑,之后再在兄弟节点为支点解右旋,之后重新进入算法。此是把当前的情况转化为情况4,而性质5得以保持,
(6)删除修复情况4:当前节点颜色是黑-黑色,它的兄弟节点是黑色,但是兄弟节点的右子是红色,兄弟节点左子的颜色任意:
解法:把兄弟节点染成当前节点父节点的颜色,把当前节点父节点染成黑色,兄弟节点右子染成黑色,之后以当前节点的父节点为支点进行左旋,此时算法结束,红黑树所有性质调整正确:
参考:https://blog.csdn.net/v_JULY_v/article/details/6105630