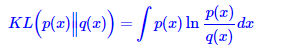- 国外7个最佳大语言模型 (LLM) API推荐
程序员后端
大型语言模型(LLM)API将彻底改变我们处理语言的方式。在深度学习和机器学习算法的支持下,LLMAPI提供了前所未有的自然语言理解能力。通过利用这些新的API,开发人员现在可以创建能够以前所未有的方式理解和响应书面文本的应用程序。下面,我们将比较从Bard到ChatGPT、PaLM等市场上顶级LLMAPI。我们还将探讨整合这些LLM的潜在用例,并考虑其对语言处理的影响。什么是大语言模型(LLM)
- Ubuntu22.4.03服务器版安装及搭建深度学习环境的问题总结
蜡笔小祎在线学习
问题集合深度学习人工智能
Ubuntu22.4.03服务器版安装流程整个流程已经有很多分享帖了,这里概述一下:下载iso制作启动U盘,按f2进入安装,选择语言,键盘布局english,ubuntuserver安装,DHCP自动配置网络(问题1),代理服务器我们没填,配置阿里云镜源http://mirrors.aliyun.com/ubuntu/,磁盘分区(问题2),设置服务器密码,安装ssh远程工具,重启reboot。可参
- 第26篇:pFedLoRA: Model-Heterogeneous Personalized Federated Learning with LoRA使用lora微调的模型异构个性化联邦学习
还不秃顶的计科生
联邦学习深度学习人工智能开发语言
第一部分:解决的问题联邦学习(FederatedLearning,FL)是一种分布式机器学习方法,允许客户端在本地数据上训练模型,同时通过中心服务器共享学习成果。传统FL框架假设客户端使用相同的模型结构(模型同构),但在实际中可能面对:统计异质性:客户端的数据分布不均(non-IID)。资源异质性:客户端硬件资源有限。模型异质性:客户端可能拥有不同的模型结构。模型异构的个性化联邦学习(MHPFL)
- 零基础学会asp.net做AI大模型网站/小程序十六:专栏总结
借雨醉东风
asp.net小程序后端
本专栏以实战为主,轻理论。如果哪里有不太懂的,可关注博主后加个人微信(平台规定文章中不能贴联系方式,需先关注博主,再加微信),后续一起交流学习。-------------------------------------正文----------------------------------------目录本专栏总结后续方向项目简介项目结构使用方法项目地址关键特点LLaMA机器学习简介使用LLaMA
- 【深度学习目标检测|YOLO算法5-1-1】YOLO家族进化史:从YOLOv1到YOLOv11的架构创新、性能优化与行业应用全解析...
985小水博一枚呀
论文解读深度学习目标检测YOLO人工智能算法架构网络
【深度学习目标检测|YOLO算法5-1-1】YOLO家族进化史:从YOLOv1到YOLOv11的架构创新、性能优化与行业应用全解析…【深度学习目标检测|YOLO算法5-1-1】YOLO家族进化史:从YOLOv1到YOLOv11的架构创新、性能优化与行业应用全解析…文章目录【深度学习目标检测|YOLO算法5-1-1】YOLO家族进化史:从YOLOv1到YOLOv11的架构创新、性能优化与行业应用全解
- Python从0到100(三十九):数据提取之正则(文末免费送书)
是Dream呀
pythonmysql开发语言
前言:零基础学Python:Python从0到100最新最全教程。想做这件事情很久了,这次我更新了自己所写过的所有博客,汇集成了Python从0到100,共一百节课,帮助大家一个月时间里从零基础到学习Python基础语法、Python爬虫、Web开发、计算机视觉、机器学习、神经网络以及人工智能相关知识,成为学习学习和学业的先行者!欢迎大家订阅专栏:零基础学Python:Python从0到100最新
- 深度学习环境配置——Anaconda安装
tyyhmtyyhm
深度学习环境配置深度学习人工智能
目录Ⅰ.Windows系统安装Anaconda1.1下载安装Ⅱ.Linux系统安装Anaconda(适用于服务器安装)2.1下载2.2安装操作系统:windows11/ubuntu20/ubuntu18更新时间:20240221Ⅰ.Windows系统安装Anaconda1.1下载安装https://www.anaconda.com/download默认安装即可。Ⅱ.Linux系统安装Anacond
- 深度学习工厂的蓝图:拆解CUDA驱动、PyTorch与OpenCV的依赖关系
时光旅人01号
深度学习pytorchopencv
想象一下,你正在建造一座深度学习工厂,这座工厂专门用于高效处理深度学习任务(如训练神经网络)和计算机视觉任务(如图像处理)。为了让工厂顺利运转,你需要搭建基础设施、安装设备、设置生产线,并配备控制台来管理整个生产过程。以下是这座工厂的详细构建过程:1.工厂的基础设施:Ubuntu比喻:Ubuntu是工厂所在的土地和建筑,提供了基础设施和运行环境。作用:提供操作系统环境,支持安装和运行各种工具和框架
- (九万字)面向2025年BOSS直聘人工智能算法工程师高频面试题解析
快撑死的鱼
人工智能回归pythonpytorch
面向2025年BOSS直聘人工智能算法工程师高频面试题解析1.机器学习(ML)理论解析机器学习是让计算机从数据中学习规律的一套方法论,包含监督学习、无监督学习和强化学习等范式。在监督学习中,给定带标签的数据,算法尝试学习从输入到输出的映射关系;无监督学习则在缺乏标签的情况下挖掘数据内在结构;强化学习则让智能体通过与环境交互、依据奖赏反馈来改进策略(Q-learning-Wikipedia)。机器学
- Centos7 搭建 Jupyter + Nginx 服务
某龙兄
pythonnginxlinuxcentos
JupyterNotebook(此前被称为IPythonnotebook)是一个交互式笔记本,支持运行40多种编程语言。JupyterNotebook的本质是一个Web应用程序,便于创建和共享文学化程序文档,支持实时代码,数学方程,可视化和markdown。用途包括:数据清理和转换,数值模拟,统计建模,机器学习等等。本文讲述如何搭建Jupyter+Nginx服务,仅供学习与交流,请勿用于商业用途一
- 人工智能与机器学习入门:基尼系数(Gini Index)和基于熵(Entropy)
基尼系数基于熵机器学习入门
在决策树应用一文中,在构建决策分类树应用决策算法时,介绍了基尼系数(GiniIndex)和基于熵(Entropy)两种算法。本文通过实例来更加深入的介绍一下这两个算法。仍然以简单的数据为例:id喜欢颜色是否有喉结身高性别1绿否165女2蓝是170男3粉否172女4绿是175男基尼系数分别对喜欢颜色是否有喉结求基尼系数如下:喜欢的颜色id喜欢颜色性别1绿女2蓝男3粉女4绿男对于姓别女分类而言,数据如
- FakeApp 技术浅析(一)
爱研究的小牛
AIGC—深度伪造虚拟现实人工智能AIGC深度学习机器学习
FakeApp是一款早期的深度伪造(Deepfake)工具,最初于2018年发布,用于生成和编辑换脸视频。尽管FakeApp已经不再更新,但它在深度伪造技术的发展中起到了重要作用。1.技术背景与理论基础1.1生成对抗网络(GANs)生成对抗网络(GANs)是深度学习领域中的一种重要模型,由生成器(Generator)和判别器(Discriminator)组成。生成器负责生成逼真的数据(如图像、视频
- DeepSeek 赋能工业软件之全流程方案
爱吃青菜的大力水手
人工智能自动化持续部署语言模型开源
deepseek赋能工业软件之全流程方案之侧重半导体FABdeepseek在工业软件中的应用场景“deepseek”大模型在工业软件领域拥有广泛的应用场景,包括以下几个方面:智能调度:利用深度学习和优化算法,根据实时数据动态调整生产计划和资源分配。它可以综合考虑订单需求、设备状态和产能限制,智能生成最优的生产排程方案,减少等待时间和切换成本。例如在汽车制造工厂,deepseek可根据订单需求和设备
- 深度学习之目标检测的常用标注工具
铭瑾熙
人工智能机器学习深度学习深度学习目标检测目标跟踪
1LabelImgLabelImg是一款开源的图像标注工具,标签可用于分类和目标检测,它是用Python编写的,并使用Qt作为其图形界面,简单好用。注释以PASCALVOC格式保存为XML文件,这是ImageNet使用的格式。此外,它还支持COCO数据集格式。2labelmelabelme是一款开源的图像/视频标注工具,标签可用于目标检测、分割和分类。灵感是来自于MIT开源的一款标注工具Label
- 34、深度学习-自学之路-深入理解-NLP自然语言处理-RNN一个简单的程序,可以从程序中理解RNN的基本思想。
小宇爱
深度学习-自学之路深度学习自然语言处理rnn
importsys,random,mathfromcollectionsimportCounterimportnumpyasnpf=open('tasks_1-20_v1/en/qa1_single-supporting-fact_train.txt','r')raw=f.readlines()f.close()tokens=list()forlineinraw[0:1000]:tokens.ap
- DeepSeek-R1 技术全景解析:从原理到实践的“炼金术配方” ——附多阶段训练流程图与核心误区澄清...
雪停时偶遇一叶春
流程图
合集-人工智能(5)1.如何改进AI模型在特定环境中的知识检索2024-09-242.深度学习与统计学中的时间序列预测2024-10-033.《使用coze搭建一个会搜索、写ppt、思维导图的Agent》2024-10-294.深入浅出:Agent如何调用工具——从OpenAIFunctionCall到CrewAI框架01-145.DeepSeek-R1技术全景解析:从原理到实践的“炼金术配方”—
- 利用Beautiful Soup和Pandas进行网页数据抓取与清洗处理实战
傻啦嘿哟
pandas
目录一、准备工作二、抓取网页数据三、数据清洗四、数据处理五、保存数据六、完整代码示例七、总结在数据分析和机器学习的项目中,数据的获取、清洗和处理是非常关键的步骤。今天,我们将通过一个实战案例,演示如何利用Python中的BeautifulSoup库进行网页数据抓取,并使用Pandas库进行数据清洗和处理。这个案例不仅适合初学者,也能帮助有一定经验的朋友快速掌握这两个强大的工具。一、准备工作在开始之
- 鸢尾花分类项目 GUI
编织幻境的妖
分类数据挖掘人工智能
1.机器学习的定义机器学习是一门人工智能的分支,专注于开发算法和统计模型,使计算机能够在没有明确编程的情况下从数据中自动学习和改进。通过识别数据中的模式和规律,机器学习系统可以做出预测或决策。常见的应用包括图像识别、语音识别、推荐系统等。2.为什么使用鸢尾花数据集(Irisdataset)鸢尾花数据集是一个经典的多类分类问题数据集,由英国统计学家和遗传学家RonaldFisher在1936年引入。
- 《神经网络与深度学习》(邱锡鹏) 内容概要【不含数学推导】
code_stream
#机器学习神经网络
第1章绪论基本概念:介绍了人工智能的发展历程及不同阶段的特点,如符号主义、连接主义、行为主义等。还阐述了深度学习在人工智能领域的重要地位和发展现状,以及其在图像、语音、自然语言处理等多个领域的成功应用。术语解释人工智能:旨在让机器模拟人类智能的技术和科学。深度学习:一种基于对数据进行表征学习的方法,通过构建具有很多层的神经网络模型,自动从大量数据中学习复杂的模式和特征。第2章机器学习概述基本概念:
- 图像识别与应用
狂踹瘸子那条好脚
python
图像识别作为人工智能领域的重要分支,近年来取得了显著进展,其中卷积神经网络(CNN)功不可没。CNN凭借其强大的特征提取能力,在图像分类、目标检测、人脸识别等任务中表现出色,成为图像识别领域的核心技术。一、卷积神经网络:图像识别的利器CNN是一种专门处理网格状数据的深度学习模型,其结构设计灵感来源于生物视觉系统。与全连接神经网络不同,CNN通过卷积层、池化层等结构,能够有效提取图像的局部特征,并逐
- 大模型如何改变教育?典型应用场景的探究与展望!
AGI大模型学习
大模型应用人工智能AI产品经理llama大模型AI大模型教程
目前,大模型在教育领域的应用主要体现在个性化学习助手、智能问答系统、内容生成与创作辅助、智能写作评估、跨语言学习支持、数学解题辅助等几个方面。大模型技术在教育领域凭借卓越的数据处理能力和深度学习技术,极大推动了教育质量的提升与教育公平的实现。分级分类的教育数据助力大模型发展在构建与优化大模型的过程中,教育数据能够帮助我们更精准地理解教育现象,更有质量地辅助教学。教育数据涵盖广泛,包括但不限于学生的
- Python中的 redis keyspace 通知_python 操作redis psubscribe(‘__keyspace@0__ ‘)
2301_82243733
程序员python学习面试
最后Python崛起并且风靡,因为优点多、应用领域广、被大牛们认可。学习Python门槛很低,但它的晋级路线很多,通过它你能进入机器学习、数据挖掘、大数据,CS等更加高级的领域。Python可以做网络应用,可以做科学计算,数据分析,可以做网络爬虫,可以做机器学习、自然语言处理、可以写游戏、可以做桌面应用…Python可以做的很多,你需要学好基础,再选择明确的方向。这里给大家分享一份全套的Pytho
- DeepSeek原理介绍以及对网络安全行业的影响
AI拉呱
Deepseek人工智能
大家好,我是AI拉呱,一个专注于人工智领域与网络安全方面的博主,现任资深算法研究员一职,兼职硕士研究生导师;热爱机器学习和深度学习算法应用,深耕大语言模型微调、量化、私域部署。曾获多次获得AI竞赛大奖,拥有多项发明专利和学术论文。对于AI算法有自己独特见解和经验。曾辅导十几位非计算机学生转行到算法岗位就业。关注评审分享一起学习更多知识。1.DeepSeek公司介绍1.1DeepSeek是什么:wh
- auto-gptq安装以及不适配软硬件环境可能出现的问题及解决方式
IT修炼家
大模型部署大模型auto-gptqcuda
目录1、auto-gptq是什么?2、auto-gptq安装3、auto-gptq不正确安装可能会出现的问题(1)爆出:`CUDAextensionnotinstalled.`(2)没有报错但是推理速度超级慢1、auto-gptq是什么?Auto-GPTQ是一种专注于量化深度学习模型的工具库。它的主要目标是通过量化技术(Quantization)将大型语言模型(LLM)等深度学习模型的大小和计算复
- 【deepseek与chatGPT辩论】辩论题: “人工智能是否应当具备自主决策能力?”
海宁不掉头发
软件工程人工智能人工智能chatgptdeepseek
探讨辩论题这个提案涉及创建一个精确的辩论题目,旨在测试deepseek的应答能力。创建辩论题目提议设计一个辩论题目以测试deepseek的应答能力。希望这个题目具有挑战性并能够测量其回应质量。好的,来一道适合深度学习的辩论题:辩论题:“人工智能是否应当具备自主决策能力?”这个话题涉及到人工智能的发展、伦理以及未来应用,可以从以下几个方面展开辩论:支持方:认为人工智能的自主决策能力能够加速科技进步,
- FOKS-TROT: 一个高效、易用的全功能开源知识图谱生成工具
柳旖岭
FOKS-TROT:一个高效、易用的全功能开源知识图谱生成工具项目简介FOKS-TROT是一个基于Python的全功能开源知识图谱生成工具,旨在帮助研究人员和开发者快速构建具有丰富信息的知识图谱。该项目由hkx3upper在GitCode上开发并维护。通过FOKS-TROT,您可以轻松地将各种数据源(如文本文件、数据库、API)转换为结构化的知识图谱,并对其进行可视化分析和机器学习任务。此外,该工
- 基于python深度学习遥感影像地物分类与目标识别、分割实践技术应用
xiao5kou4chang6kai4
深度学习遥感勘测python深度学习分类
专题一:深度学习发展与机器学习深度学习的历史发展过程机器学习,深度学习等任务的基本处理流程梯度下降算法讲解不同初始化,学习率对梯度下降算法的实例分析从机器学习到深度学习算法专题二深度卷积网络、卷积神经网络、卷积运算的基本原理池化操作,全连接层,以及分类器的作用BP反向传播算法的理解一个简单CNN模型代码理解特征图,卷积核可视化分析专题三TensorFlow与keras介绍与入门TensorFlow
- LLM与知识图谱融合:智能运维知识库构建
AI天才研究院
DeepSeekR1&大数据AI人工智能大模型AI大模型企业级应用开发实战AI实战计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
1.背景介绍随着信息技术的飞速发展,IT运维管理面临着越来越大的挑战。海量的设备、复杂的网络环境、日益增长的数据量,使得传统的运维方式难以满足需求。为了提高运维效率和质量,智能运维应运而生。智能运维的核心是将人工智能技术应用于运维领域,通过机器学习、深度学习等算法,实现自动化、智能化的运维管理。其中,大语言模型(LLM)和知识图谱是两个重要的技术方向。LLM能够理解和生成自然语言,可以用于构建智能
- 机器学习·文本数据读写处理
AAA顶置摸鱼
python深度学习机器学习人工智能数据处理
前言在自然语言处理的第一步,需要面对的是各种各样以不同形式表现的文本数据,比如,txt、Excel中的表格数据,还有无法直接打开的pkl文件等。针对这些不同类型的数据,可以基于Python中的基本功能函数或者调用某些库进行读写以及作一些基本的处理。一、文本数据读写方法1.读写TXT文件读取方法:read():读取整个文件,返回字符串。readline():逐行读取,返回字符串。readlines(
- 深度应用场景:DeepSeek —— 探索AI赋能的智慧未来
人工智能专属驿站
人工智能
深度应用场景:DeepSeek——探索AI赋能的智慧未来随着人工智能的迅猛发展,数据的价值已不再局限于简单的存储与处理,它们正变得更加智能与高效。DeepSeek,这一创新的AI技术平台,正以其独特的深度学习能力,开启了各行各业的智能化变革。让我们走进一个由DeepSeek打造的深度应用场景,探索它如何推动未来的发展。1.智能医疗:精准诊断,拯救生命想象一下,医生们不再是唯一的诊断专家,而是与AI
- Nginx负载均衡
510888780
nginx应用服务器
Nginx负载均衡一些基础知识:
nginx 的 upstream目前支持 4 种方式的分配
1)、轮询(默认)
每个请求按时间顺序逐一分配到不同的后端服务器,如果后端服务器down掉,能自动剔除。
2)、weight
指定轮询几率,weight和访问比率成正比
- RedHat 6.4 安装 rabbitmq
bylijinnan
erlangrabbitmqredhat
在 linux 下安装软件就是折腾,首先是测试机不能上外网要找运维开通,开通后发现测试机的 yum 不能使用于是又要配置 yum 源,最后安装 rabbitmq 时也尝试了两种方法最后才安装成功
机器版本:
[root@redhat1 rabbitmq]# lsb_release
LSB Version: :base-4.0-amd64:base-4.0-noarch:core
- FilenameUtils工具类
eksliang
FilenameUtilscommon-io
转载请出自出处:http://eksliang.iteye.com/blog/2217081 一、概述
这是一个Java操作文件的常用库,是Apache对java的IO包的封装,这里面有两个非常核心的类FilenameUtils跟FileUtils,其中FilenameUtils是对文件名操作的封装;FileUtils是文件封装,开发中对文件的操作,几乎都可以在这个框架里面找到。 非常的好用。
- xml文件解析SAX
不懂事的小屁孩
xml
xml文件解析:xml文件解析有四种方式,
1.DOM生成和解析XML文档(SAX是基于事件流的解析)
2.SAX生成和解析XML文档(基于XML文档树结构的解析)
3.DOM4J生成和解析XML文档
4.JDOM生成和解析XML
本文章用第一种方法进行解析,使用android常用的DefaultHandler
import org.xml.sax.Attributes;
- 通过定时任务执行mysql的定期删除和新建分区,此处是按日分区
酷的飞上天空
mysql
使用python脚本作为命令脚本,linux的定时任务来每天定时执行
#!/usr/bin/python
# -*- coding: utf8 -*-
import pymysql
import datetime
import calendar
#要分区的表
table_name = 'my_table'
#连接数据库的信息
host,user,passwd,db =
- 如何搭建数据湖架构?听听专家的意见
蓝儿唯美
架构
Edo Interactive在几年前遇到一个大问题:公司使用交易数据来帮助零售商和餐馆进行个性化促销,但其数据仓库没有足够时间去处理所有的信用卡和借记卡交易数据
“我们要花费27小时来处理每日的数据量,”Edo主管基础设施和信息系统的高级副总裁Tim Garnto说道:“所以在2013年,我们放弃了现有的基于PostgreSQL的关系型数据库系统,使用了Hadoop集群作为公司的数
- spring学习——控制反转与依赖注入
a-john
spring
控制反转(Inversion of Control,英文缩写为IoC)是一个重要的面向对象编程的法则来削减计算机程序的耦合问题,也是轻量级的Spring框架的核心。 控制反转一般分为两种类型,依赖注入(Dependency Injection,简称DI)和依赖查找(Dependency Lookup)。依赖注入应用比较广泛。
- 用spool+unixshell生成文本文件的方法
aijuans
xshell
例如我们把scott.dept表生成文本文件的语句写成dept.sql,内容如下:
set pages 50000;
set lines 200;
set trims on;
set heading off;
spool /oracle_backup/log/test/dept.lst;
select deptno||','||dname||','||loc
- 1、基础--名词解析(OOA/OOD/OOP)
asia007
学习基础知识
OOA:Object-Oriented Analysis(面向对象分析方法)
是在一个系统的开发过程中进行了系统业务调查以后,按照面向对象的思想来分析问题。OOA与结构化分析有较大的区别。OOA所强调的是在系统调查资料的基础上,针对OO方法所需要的素材进行的归类分析和整理,而不是对管理业务现状和方法的分析。
OOA(面向对象的分析)模型由5个层次(主题层、对象类层、结构层、属性层和服务层)
- 浅谈java转成json编码格式技术
百合不是茶
json编码java转成json编码
json编码;是一个轻量级的数据存储和传输的语言
在java中需要引入json相关的包,引包方式在工程的lib下就可以了
JSON与JAVA数据的转换(JSON 即 JavaScript Object Natation,它是一种轻量级的数据交换格式,非
常适合于服务器与 JavaScript 之间的数据的交
- web.xml之Spring配置(基于Spring+Struts+Ibatis)
bijian1013
javaweb.xmlSSIspring配置
指定Spring配置文件位置
<context-param>
<param-name>contextConfigLocation</param-name>
<param-value>
/WEB-INF/spring-dao-bean.xml,/WEB-INF/spring-resources.xml,
/WEB-INF/
- Installing SonarQube(Fail to download libraries from server)
sunjing
InstallSonar
1. Download and unzip the SonarQube distribution
2. Starting the Web Server
The default port is "9000" and the context path is "/". These values can be changed in &l
- 【MongoDB学习笔记十一】Mongo副本集基本的增删查
bit1129
mongodb
一、创建复本集
假设mongod,mongo已经配置在系统路径变量上,启动三个命令行窗口,分别执行如下命令:
mongod --port 27017 --dbpath data1 --replSet rs0
mongod --port 27018 --dbpath data2 --replSet rs0
mongod --port 27019 -
- Anychart图表系列二之执行Flash和HTML5渲染
白糖_
Flash
今天介绍Anychart的Flash和HTML5渲染功能
HTML5
Anychart从6.0第一个版本起,已经逐渐开始支持各种图的HTML5渲染效果了,也就是说即使你没有安装Flash插件,只要浏览器支持HTML5,也能看到Anychart的图形(不过这些是需要做一些配置的)。
这里要提醒下大家,Anychart6.0版本对HTML5的支持还不算很成熟,目前还处于
- Laravel版本更新异常4.2.8-> 4.2.9 Declaration of ... CompilerEngine ... should be compa
bozch
laravel
昨天在为了把laravel升级到最新的版本,突然之间就出现了如下错误:
ErrorException thrown with message "Declaration of Illuminate\View\Engines\CompilerEngine::handleViewException() should be compatible with Illuminate\View\Eng
- 编程之美-NIM游戏分析-石头总数为奇数时如何保证先动手者必胜
bylijinnan
编程之美
import java.util.Arrays;
import java.util.Random;
public class Nim {
/**编程之美 NIM游戏分析
问题:
有N块石头和两个玩家A和B,玩家A先将石头随机分成若干堆,然后按照BABA...的顺序不断轮流取石头,
能将剩下的石头一次取光的玩家获胜,每次取石头时,每个玩家只能从若干堆石头中任选一堆,
- lunce创建索引及简单查询
chengxuyuancsdn
查询创建索引lunce
import java.io.File;
import java.io.IOException;
import org.apache.lucene.analysis.Analyzer;
import org.apache.lucene.analysis.standard.StandardAnalyzer;
import org.apache.lucene.document.Docume
- [IT与投资]坚持独立自主的研究核心技术
comsci
it
和别人合作开发某项产品....如果互相之间的技术水平不同,那么这种合作很难进行,一般都会成为强者控制弱者的方法和手段.....
所以弱者,在遇到技术难题的时候,最好不要一开始就去寻求强者的帮助,因为在我们这颗星球上,生物都有一种控制其
- flashback transaction闪回事务查询
daizj
oraclesql闪回事务
闪回事务查询有别于闪回查询的特点有以下3个:
(1)其正常工作不但需要利用撤销数据,还需要事先启用最小补充日志。
(2)返回的结果不是以前的“旧”数据,而是能够将当前数据修改为以前的样子的撤销SQL(Undo SQL)语句。
(3)集中地在名为flashback_transaction_query表上查询,而不是在各个表上通过“as of”或“vers
- Java I/O之FilenameFilter类列举出指定路径下某个扩展名的文件
游其是你
FilenameFilter
这是一个FilenameFilter类用法的例子,实现的列举出“c:\\folder“路径下所有以“.jpg”扩展名的文件。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
- C语言学习五函数,函数的前置声明以及如何在软件开发中合理的设计函数来解决实际问题
dcj3sjt126com
c
# include <stdio.h>
int f(void) //括号中的void表示该函数不能接受数据,int表示返回的类型为int类型
{
return 10; //向主调函数返回10
}
void g(void) //函数名前面的void表示该函数没有返回值
{
//return 10; //error 与第8行行首的void相矛盾
}
in
- 今天在测试环境使用yum安装,遇到一个问题: Error: Cannot retrieve metalink for repository: epel. Pl
dcj3sjt126com
centos
今天在测试环境使用yum安装,遇到一个问题:
Error: Cannot retrieve metalink for repository: epel. Please verify its path and try again
处理很简单,修改文件“/etc/yum.repos.d/epel.repo”, 将baseurl的注释取消, mirrorlist注释掉。即可。
&n
- 单例模式
shuizhaosi888
单例模式
单例模式 懒汉式
public class RunMain {
/**
* 私有构造
*/
private RunMain() {
}
/**
* 内部类,用于占位,只有
*/
private static class SingletonRunMain {
priv
- Spring Security(09)——Filter
234390216
Spring Security
Filter
目录
1.1 Filter顺序
1.2 添加Filter到FilterChain
1.3 DelegatingFilterProxy
1.4 FilterChainProxy
1.5
- 公司项目NODEJS实践0.1
逐行分析JS源代码
mongodbnginxubuntunodejs
一、前言
前端如何独立用nodeJs实现一个简单的注册、登录功能,是不是只用nodejs+sql就可以了?其实是可以实现,但离实际应用还有距离,那要怎么做才是实际可用的。
网上有很多nod
- java.lang.Math
liuhaibo_ljf
javaMathlang
System.out.println(Math.PI);
System.out.println(Math.abs(1.2));
System.out.println(Math.abs(1.2));
System.out.println(Math.abs(1));
System.out.println(Math.abs(111111111));
System.out.println(Mat
- linux下时间同步
nonobaba
ntp
今天在linux下做hbase集群的时候,发现hmaster启动成功了,但是用hbase命令进入shell的时候报了一个错误 PleaseHoldException: Master is initializing,查看了日志,大致意思是说master和slave时间不同步,没办法,只好找一种手动同步一下,后来发现一共部署了10来台机器,手动同步偏差又比较大,所以还是从网上找现成的解决方
- ZooKeeper3.4.6的集群部署
roadrunners
zookeeper集群部署
ZooKeeper是Apache的一个开源项目,在分布式服务中应用比较广泛。它主要用来解决分布式应用中经常遇到的一些数据管理问题,如:统一命名服务、状态同步、集群管理、配置文件管理、同步锁、队列等。这里主要讲集群中ZooKeeper的部署。
1、准备工作
我们准备3台机器做ZooKeeper集群,分别在3台机器上创建ZooKeeper需要的目录。
数据存储目录
- Java高效读取大文件
tomcat_oracle
java
读取文件行的标准方式是在内存中读取,Guava 和Apache Commons IO都提供了如下所示快速读取文件行的方法: Files.readLines(new File(path), Charsets.UTF_8); FileUtils.readLines(new File(path)); 这种方法带来的问题是文件的所有行都被存放在内存中,当文件足够大时很快就会导致
- 微信支付api返回的xml转换为Map的方法
xu3508620
xmlmap微信api
举例如下:
<xml>
<return_code><![CDATA[SUCCESS]]></return_code>
<return_msg><![CDATA[OK]]></return_msg>
<appid><
![]() 通过一个编码器(Encoder)输入到一个分布隐变量(latent variable)空间上去,这个隐变量空间猛地一听有点唬人,其实可以把它当成一个分布,比如正态分布。然后从这个隐空间上采样一个数据,再通过解码器(Decoder)输出
通过一个编码器(Encoder)输入到一个分布隐变量(latent variable)空间上去,这个隐变量空间猛地一听有点唬人,其实可以把它当成一个分布,比如正态分布。然后从这个隐空间上采样一个数据,再通过解码器(Decoder)输出 ![]() ,使得
,使得 ![]() 与
与 ![]() 尽可能的一样。
尽可能的一样。,是不是还对应着原来的
。
![]() ,我们希望在给定
,我们希望在给定 ![]() 的条件下去推出
的条件下去推出 ![]() 的分布,即
的分布,即 ![]() 。
。![]() 无法计算,因为
无法计算,因为 ![]() 无法计算。所以我们用一个我们可求解的分布
无法计算。所以我们用一个我们可求解的分布 ![]() 去近似这个
去近似这个 ![]() 。
。![]() 和
和 ![]() 近似,KL散度公式就变成了,
近似,KL散度公式就变成了,![]() 是已经给定的,所以虽然我不知道
是已经给定的,所以虽然我不知道 ![]() 是多少,但它的确肯定是个定值,于是最小化
是多少,但它的确肯定是个定值,于是最小化![]() 相当于最小化后两项
相当于最小化后两项![]()
![]() ,等于最大化
,等于最大化![]() ,也就是说最大化
,也就是说最大化![]()
![]() 与原始样本
与原始样本 ![]() 的最接近。
的最接近。![]() 和先验分布
和先验分布 ![]() 尽量接近,这里的后验分布是我们可求解的,先验分布
尽量接近,这里的后验分布是我们可求解的,先验分布 ![]() 和 一开始的
和 一开始的![]() 不是一回事,一开始的
不是一回事,一开始的![]() 我们是没办法知道的,而这个先验分布
我们是没办法知道的,而这个先验分布![]() 我们是可以人为定义的,在论文中将这个先验分布定义为标准正态分布
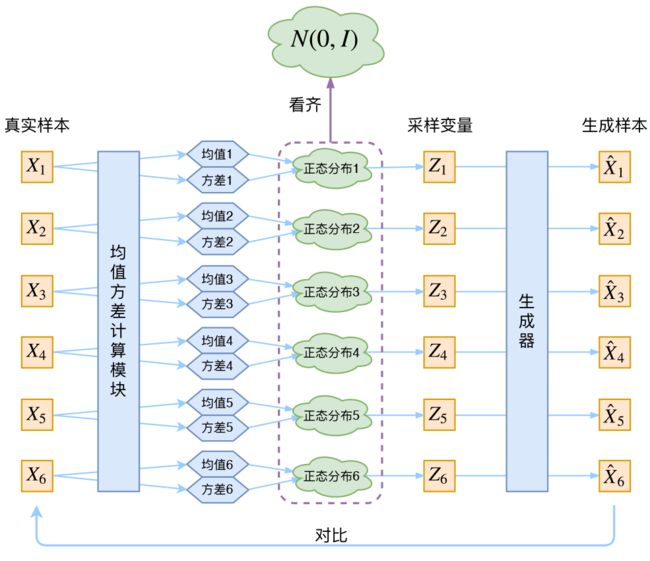
我们是可以人为定义的,在论文中将这个先验分布定义为标准正态分布 ![]() ,而 后验分布
,而 后验分布 ![]() 其实就是图二当中的这一部分,如下图,它是可以通过神经网络得到的。
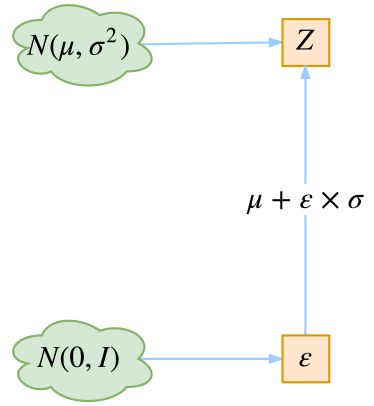
其实就是图二当中的这一部分,如下图,它是可以通过神经网络得到的。![]() 都是采样得到的,但是 “采样” 这个操作是不可导的,而采样的结果是可导的。所以利用
都是采样得到的,但是 “采样” 这个操作是不可导的,而采样的结果是可导的。所以利用![]() 中采样一个Z,相当于从
中采样一个Z,相当于从![]() 中采样一个ε,然后让
中采样一个ε,然后让 ![]() 。
。![]() 采样变成了从
采样变成了从![]() 中采样,然后通过参数变换得到从
中采样,然后通过参数变换得到从![]() 中采样的结果。这样一来,“采样” 这个操作就不用参与梯度下降了,改为采样的结果参与,使得整个模型可训练了。
中采样的结果。这样一来,“采样” 这个操作就不用参与梯度下降了,改为采样的结果参与,使得整个模型可训练了。