动手学深度学习PyTorch版 | （1）线性回归、softmax与分类、多层感知机

一、线性回归

线性回归输出是一个连续值，因此适用于回归问题。回归问题在实际中很常见，如预测房屋价格、⽓温、销售额等连续值的问题。与回归问题不同，分类问题中模型的最终输出是⼀个离散值。我们所说的图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题都属于分类问题的范畴。softmax回归则适用于分类问题。

-线性回归的基本要素

以一个简单的房屋价格预测作为例子来解释线性回归的基本要素。⽬标是预测一栋房⼦的售出价格(元)。这个价格取决于很多因素，如房屋状况、地段、市场行情等。为了简单起见，这里假设价格只取决于房屋状况的两个因素，即⾯积(平⽅米)和房龄(年)。

-线性回归的从零实现

先引用必须的包

import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random  

—生成数据集

生成一个1000样本的数据集，下面是用来生成数据的线性关系：

num_inputs = 2
num_examples = 1000
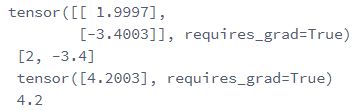
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
# print(labels)
print(labels.shape)
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                       dtype=torch.float32)
# print(labels)
print(labels.shape)

我们构造了一个简单的⼈工训练数据集，能够直观比较学到的参数和真实的模型参数的区别。设训练数据集样本数为1000，输入个数(特征数)为2。给定随机⽣成的批量样本特征x,我们使用线性回归模型真实权重w = [2, -3.4],和偏差 b=4.2，以及一个随机噪声项来生成标签：

其中噪声项服从均值为0、标准差为0.01的正态分布。噪声代表了数据集中无意义的干扰。
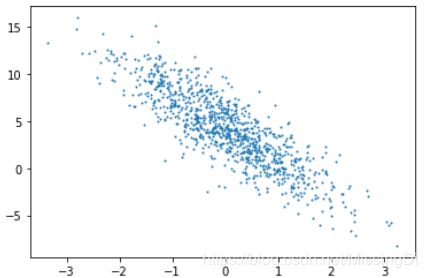
通过⽣成第一个特征features[:,0]和标签labels的散点图，可以更直观地观察两者间的线性关系:

plt.scatter(features[:,0].numpy(), labels.numpy(),1)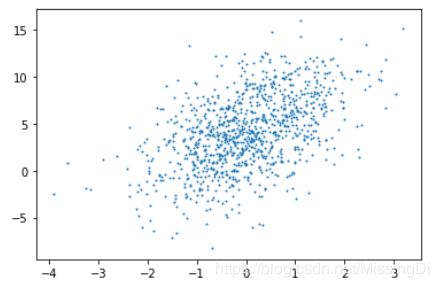

生成第二个特征 features[:,1]和标签labels的散点图：

plt.scatter(features[:,1].numpy(), labels.numpy(),1)

—读取数据集

def data_iter(batch_size,features,labels):   #这里batch_size：10  features：（1000，2）的矩阵 labels是经过线性回归公式计算得到的预测值，labels=X*w+b
    num_examples = len(features)  # # features:(1000,2)  len(features):1000
    print(num_examples) # 1000
    indices = list(range(num_examples))  # [0,1,2...,999]
    random.shuffle(indices) # 打乱顺序
    for i in range(0,num_examples,batch_size):   # 0-1000，step=10  [0,10,20,...,999]
        j = torch.LongTensor(indices[i:min(i + batch_size, num_examples)])  # 取indice值，并且返回成一个tensor。最后一次可能不足一个batch，i + batch_size 肯定小于 num_examples,故用min函数
        yield features.index_select(0,j),labels.index_select(0,j)  # 0代表按行取值，1代表按列取值；这里（0，j）代表按行取行索引为j的features元素

yield的理解请参见：https://blog.csdn.net/mieleizhi0522/article/details/82142856
很好理解的，感谢博主大大！
index_select( )的理解请参见：https://www.yzlfxy.com/jiaocheng/python/337619.html

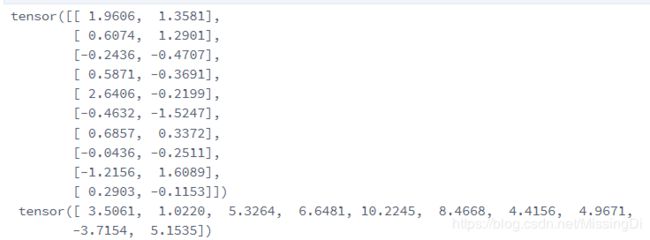
接着读取第一个⼩批量数据样本并打印。每个批量特征的形状为(10, 2)，分别对应批量⼤小10和特征个数2;标签形状为批量值⼤小。

batch_size = 10
for X, y in data_iter(batch_size,features,labels):
    print(X,'\n',y)
    break

—初始化模型参数

我们将权值初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0。

w = torch.tensor(np.random.normal(0,0.01,(num_inputs,1)),dtype=torch.float32) # num_inputs是特征个数2
b = torch.zeros(1,dtype=torch.float32)

之后模型训练中，后向传播需要对这些参数求梯度来迭代参数的值，因此我们要让它们的requires_grad=True

w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

所有的tensor都有.requires_grad属性,可以设置这个属性.为True或者False。如果想改变这个属性，就调用tensor.requires_grad_()方法
requires_grad的详细介绍请见：
https://blog.csdn.net/Xs_55555/article/details/79742276

—定义模型

下⾯是线性回归的⽮量计算表达式的实现。我们使⽤ mm 函数做矩阵乘法：

def linreg(X,w,b):
    return torch.mm(X,w) + b # mm 即为矩阵相乘，两个矩阵的维度需满足(i,n) * (n,j)，最终得到的矩阵维度为i*j 

pytorch的常见乘法：
PyTorch 对应点相乘、矩阵相乘

—定义损失函数

使用均方误差损失函数：

在实现中，我们需要把真实值y变形成预测值y_hat的形状。以下函数返回的结果也将和预测值y_hat的形状相同

def squared_loss(y_hat,y):
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

view()函数是将y的形状和y_hat的size一样，详解见：
torch.view()详解及-1参数是什么意思

—定义优化函数

以下的sgd函数实现了上一节中介绍的⼩批量随机梯度下降算法。它通过不断迭代模型参数来优化损失 函数。这⾥自动求梯度模块计算得来的梯度是一个批量样本的梯度和。我们将它除以批量⼤小来得到平均值。

def sgd(params,lr,batch_size):
    for param in params:
        param.data -= lr * param.grad / batch_size

—训练模型

在训练中，我们将多次迭代模型参数。在每次迭代中，我们根据当前读取的⼩批量数据样本(特征X和标签y)，通过调⽤反向函数backward计算小批量随机梯度，并调用优化算法sgd迭代模型参数。由于我们之前设批量⼤小 batch_size为10，每个小批量量的损失loss的形状为(10, 1)。由于变量l并不是一个标量，所以我们可以调⽤.sum()将其求和得到⼀一个标量，再运行l.backward()得到该变量有关模型参数的梯度。注意在每次更新完参数后不要忘了将参数的梯度清零。

在⼀个迭代周期(epoch)中，我们将完整遍历⼀遍data_iter函数，并对训练数据集中所有样本都使⽤一次(假设样本数能够被批量⼤小整除)。这里的迭代周期个数 num_epochs和学习率lr都是超参数，分别设3和0.03。在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得 越⼤模型可能越有效，但是训练时间可能过长。而有关学习率对模型的影响，我们会在后面详细介绍。

lr = 0.03 # 学习率
num_epochs = 5
net = linreg
loss = squared_loss

# training
for epoch in range(num_epochs):  # 训练模型一共需要num_epochs个迭代周期,在每一轮，数据集中所有的样本都会被用一次
    for X,y in data_iter(batch_size,features,labels):
        l = loss(net(X,w,b),y).sum()  # l是有关小批量X和y的损失
        l.backward()  # 小批量的损失对模型参数求梯度
        sgd([w,b],lr,batch_size)  # 使用小批量随机梯度下降迭代模型参数
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features,w,b),labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

backward()函数详解见博客：
PyTorch的学习笔记02 - backward( )函数
训练完成后，我们可以比较学到的参数和⽤来⽣成训练集的真实参数。它们应该很接近

print(w, '\n',true_w,'\n', b,'\n', true_b)

-线性回归使用pyTorch的简洁实现

在本节中，我们将介绍如何使用PyTorch更⽅便地实现线性回归的训练。

—生成数据集

在这里，生成数据集 和 从零实现的方法一样

num_inputs = 2
num_examples = 1000
true_w = [2,-3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)),dtype=torch.float)
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float)

—读取数据集

PyTorch提供了data包来读取数据。由于data常⽤作变量名，我们将导入的data模块⽤Data代替。在每⼀次迭代中，我们将随机读取包含10个数据样本的⼩批量。

import torch.utils.data as Data
batch_size = 10
dataset = Data.TensorDataset(features,labels)  # 将训练数据的特征和标签组合 构建dataset
data_iter = Data.DataLoader(
    dataset = dataset,
    batch_size = batch_size,
    shuffle=True,
    num_workers = 2,   # read data in multithreading
    )

这⾥的data_iter使⽤跟上⼀节中的⼀样。让我们读取并打印第一个⼩批量数据样本

for X,y in data_iter:
    print(X,'\n',y)
    break

—定义模型

之前已经导⼊模块torch.nn。实际上，“nn”是neural networks(神经网络)的缩写。顾名思义，该模块定义了⼤量神经网络的层。之前我们已经⽤过了autograd ，⽽nn就是利用autograd来定义模型。 nn的核⼼数据结构是Module ，它是⼀个抽象概念，既可以表示神经⽹络中的某个层(layer)， 也可以表示⼀个包含很多层的神经⽹络。在实际使⽤中，最常⻅的做法是继承nn.Module ，撰写⾃己的⽹络/层。⼀个nn.Module实例应该包含一些层以及返回输出的前向传播(forward)方法。下⾯先来看看如何用nn.Module实现一个线性回归模型

class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()      # call father function to init 调用父亲函数进行初始化 
        self.linear = nn.Linear(n_feature, 1)
        # function prototype: `torch.nn.Linear(in_features, out_features, bias=True)`
    def forward(self, x):
        y = self.linear(x)
        return y
net = LinearNet(num_inputs)
print(net)

# ways to init a multilayer network

# method one
net = nn.Sequential(
    nn.Linear(num_inputs,1)
    # other layers can be added here
    )

# method two
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......

#  method three
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
          ('linear', nn.Linear(num_inputs, 1))
          # ......
        ]))

print(net)
print(net[0])

—初始化模型参数

使⽤net前，我们需要初始化模型参数，如线性回归模型中的权重和偏差，Pytorch在init模块中提供了很多参数初始化方法。这⾥的init是initializer的缩写形式。我们通过init.normal_把权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。（如果不自行初始化参数，将使用net默认初始化的参数）

from torch.nn import init
init.normal_(net[0].weight,mean=0.0,std=0.01)
init.constant_(net[0].bias,val=0.0)  # 也可以直接修改bias的data: net[0].bias.data.fill_(0)

for param in net.parameters():
    print(param)

—定义损失函数

PyTorch在nn模块中提供了各种损失函数，这些损失函数可看作是⼀种特殊的层，PyTorch也将这些损失函数实现为nn.Module的子类。我们现在使⽤它提供的均⽅误差损失作为模型的损失函数。

loss = nn.MSELoss()    # nn built-in squared loss function
                       # function prototype: `torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')`

—定义优化算法

同样，我们也⽆无须⾃己实现⼩批量随机梯度下降算法。 torch.optim模块提供了很多常⽤的优化算法 ⽐如SGD、Adam和RMSProp等。下面我们创建一个⽤于优化net所有参数的优化器实例，并指定学习率为0.03的⼩批量随机梯度下降(SGD)为优化算法。

import torch.optim as optim
optimizer = optim.SGD(net.parameters(),lr=0.03)  # built-in random gradient descent function
print(optimizer)  # function prototype: `torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)`

我们还可以为不同⼦⽹络设置不同的学习率，这在finetune时经常⽤到。例:

# 为不同子网络设置不同的学习率
# optimizer =optim.SGD([
#                 # 如果对某个参数不指定学习率，就使用最外层的默认学习率
#                 {'params': net.subnet1.parameters()},  # lr=0.03
#                 {'params': net.subnet2.parameters(), 'lr': 0.01}
#             ], lr=0.03)

—训练

在使⽤Gluon训练模型时，我们通过调⽤optim实例的step()函数来迭代模型参数。按照⼩批量随机梯度下降的定义，我们在 函数中指明批量⼤小，从⽽对批量中样本梯度求平均

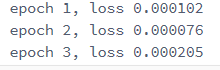
num_epochs = 3
for epoch in range(1,num_epoch + 1):
    for X,y in data_iter:
        output = net(X)
        l = loss(output,y.view(-1,1))
        optimmizer.zero_grad()  # 梯度清零，等价于net.zero_grad()
        l.backward()    # 后向传播计算梯度
        optimizer.step()  # 完成权重的更新
    print('epoch %d, loss %f' % (epoch, l.item()))  

optimizer.step()解释见：
pytorch – loss.backward()和optimizer.step()之间的连接

下⾯我们分别⽐较学到的模型参数和真实的模型参数。我们从net获得需要的层，并访问其权重weight和偏差bias，学到的参数和真实的参数很接近。

# method one
dense = net[0]
print(true_w, dense.weight.data)
print(true_b, dense.bias.data)

# method two
print(true_w, net[0].weight.data)
print(true_b, net[0].bias.data)

- 小结

1）从零实现：可以更好的理解模型，理解神经网络底层的原理
2）使⽤PyTorch可以更简洁地实现模型。
3）torch.utils.data模块提供了有关数据处理的工具，torch.nn模块定义了大量神经网络层，torch.nn.init模块定义了各种初始化方法,torch.optim模块提供了模型参数优化的各种方法。

二、Softmax与分类

内容包含：
1.softmax回归的基本概念
2.如何获取Fashion-MNIST数据集和读取数据
3.softmax回归模型的从零开始实现，实现一个对Fashion-MNIST训练集中的图像数据进行分类的模型
4.使用pytorch重新实现softmax回归模型

softmax回归的基本概念

分类问题

一个简单的图像分类问题，输入图像的高和宽均为2像素，色彩为灰度。

图像中的4像素分别记为x1,x2,x3,x4x1,x2,x3,x4。

假设真实标签为狗、猫或者鸡，这些标签对应的离散值为y1,y2,y3y1,y2,y3。

我们通常使用离散的数值来表示类别，例如y1=1,y2=2,y3=3y1=1,y2=2,y3=3。
权重矢量
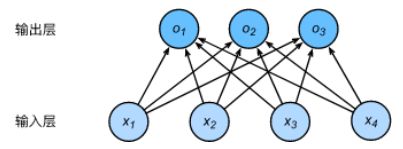
o1=x1w11+x2w21+x3w31+x4w41+b1o1=x1w11+x2w21+x3w31+x4w41+b1 o2=x1w12+x2w22+x3w32+x4w42+b2o2=x1w12+x2w22+x3w32+x4w42+b2 o3=x1w13+x2w23+x3w33+x4w43+b3o3=x1w13+x2w23+x3w33+x4w43+b3

神经网络图
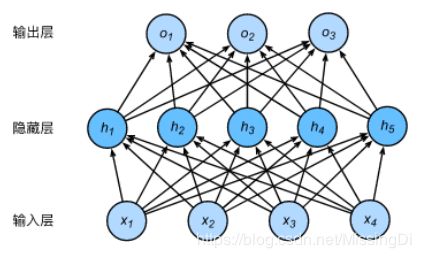
下图用神经网络图描绘了上面的计算。softmax回归同线性回归一样，也是一个单层神经网络。由于每个输出o1,o2,o3o1,o2,o3的计算都要依赖于所有的输入x1,x2,x3,x4x1,x2,x3,x4，softmax回归的输出层也是一个全连接层。

三、多层感知机

1.多层感知机的基本知识
2.使用多层感知机图像分类的从零开始的实现
3.使用pytorch的简洁实现
深度学习主要关注多层模型。在这里，我们将以多层感知机（multilayer perceptron，MLP）为例，介绍多层神经网络的概念。

隐藏层

下图展示了一个多层感知机的神经网络图，它含有一个隐藏层，该层中有5个隐藏单元。