DEEP GRAPH INFOMAX

ABSTRACT

• 从摘要得出本文特点：
  • Deep Graph Infomax (DGI)是无监督学习；
  • 用已有的GCNs来做：最大化邻近表示（patch representation）与对应的高阶图摘要（high-level summaries of graphs）之间的互信息（MI）；
  • 与之前的GCNs的不同之处是：DGI目标函数与之前的随机游走目标函数不一样。到底怎么不一样继续。。。

DGI METHODOLOGY

• 学一个编码器如下:
  

拿来用： $\mathbf{\epsilon }(X,A)=H=\{h_1,h_2,\dots ,h_N\}$：表示输入属性矩阵与邻接矩阵，输出为每个节点的高阶表示。这个编码器就是GCNs，为什么用这个呢，因为这个卷积能把邻近节点的信息汲取到这个点上，所以本文称这个点的表示$h_i$为patch representation。

• 局部-全局 互信息最大化：

  • 编码器学习需要一个目标函数，这个目标函数的目的是最大化互信息：每个节点的局部表示（也就是$h_i$）与整个图的全局信息内容（表示为向量 $s$）；这样的话每个节点的表示就能用一定的全局信息在里面了。
  • 这个$s$怎么来？用一个函数 $\mathcal{R}$ 直接映射出来， $s=\mathcal{R}(\mathbf{\epsilon }(X,A))$，$s\in R^F$,表示一个图级别的摘要。

• 还需要一个判别器$D$，拿来用：$D(h_i,s)$ 表示分配给这对pair的概率分数；注意 $h_i$ 是一个点的嵌入表示，$s$是整个图的摘要，因此每一个点都要与$s$做这么一个计算；

• 还差什么：负样本？负样本用在判别器上，负样来来源于一个假图$(\bar{X},\bar{A})$上生成的${\bar{h}}_i$结合上面的$s$来作为负样本；这样的话，这是一个二分类的判别器（二元交叉熵(BCE)损失）：
  

---

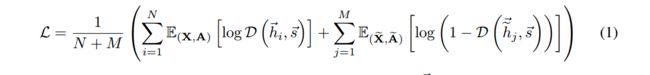
• 注：二元交叉熵：可以参考(这里)：主要是看怎么由交叉熵推出二元分类的损失函数：

其中交叉熵（cross entropy）：
$$\mathbb{H}(p,q)=-\sum _{k=1}^K{p}_k\log q_k$$
给一个例子，绿点正样本，红点负样本，用一个逻辑回归分类，拟合的分类曲线是一条sigmoid曲线如图，绿色的条代表计算这个点是正样本的概率，那么对于负样本，就是1减去这个绿色条的概率，所以负样本的概率计算后被1减去。

根据交叉熵公式，当每个点的出现是均匀时候,即$p_k=\frac{1}{K}$，有：

$$\mathbb{H}(p,q)=-\frac{1}{N}\sum _{k=1}^K\log q_k$$

据此，计算正负样本的交叉熵时，有：

$$\mathbb{H}(p,q)=-\frac{1}{N_{pos}+N_{neg}}\left[\sum _{k=1}^{N_{pos}}\log q_k+\sum _{k=1}^{N_{neg}}\log (1-q_k)\right]$$
注：上面的损失函数类似于生成对抗网络的损失函数：

$$V(D,G)=E_{x\sim p_{data}(x)}[\log D(x)]+E_{z\sim p_z(z)}[\log (1-G(z))]$$
生成对抗网络最终是两个KL散度-log(4)。
更多在这：https://blog.csdn.net/NockinOnHeavensDoor/article/details/80220692

---

THEORETICAL MOTIVATION

• 为什么使这种二元熵作为目标函数分类不错?
  引理：给定了$K$个图，每个图的节点表示集合为$X^{(k)}$，每个图从分布$p(X)$中被选中概率是均匀的；联合概率与边缘概率之间的最优分类器在类平衡的条件下，错误的上限是

$$\text{Err*}=1/2\sum _{k=1}^{|X|}p(s^{(k)}{)}^2$$

这个前提是生成图摘要$s^{(k)}$的函数$R$是单射函数。原给定如下图：

证明：${\mathcal{Q}}^{(K)}$是全部图的集合，满足${\mathcal{Q}}^{(K)}=\{X^{(j)}|R(X^{(j)})=s^{(k)}\}$，从边缘分布中采样，这个样本当做联合分布中得到的样本，有：

$$p(s^{(k)})\sum _{s}p(X^{(k)},s)=p(s^{(k)})p(X^{(k)}|s^{(k)})p(s^{(k)})$$

这是因为，从别的图如$X^{(k+j)}$也会被$R$映射为$s^{(k)}$，但是$R$单射的条件下，只能在图$X^{(k)}$上映射得到$s^{(k)}$；

后面推出结论从联合分布中采样的概率大于从边缘分布乘积中采样代替联合分布的概率。就像一个箱子里有2个红球1个蓝球，分类器分类出球为红球的概率大，也就是分类器更容易分类红球，分类正确的概率是$2/3$,但是分类是不是蓝球，正确的概率是$1/3$,那么分类器出错的概率是红球小于蓝球，这么说的话，分类器分类一个样本来自联合分布的出错概率更小。

这个分类器的错误率是从边缘分布中采样，这个样本当做联合分布中得到的样本，误差是

$$\text{Err*}=1/2\sum _{k=1}^{|X|}p(s^{(k)}{)}^2$$
这里的$1/2$是因为一个分类器对蓝球红球的分类是无偏的，都是均匀的，但是抽出来蓝球红球的概率是不一样的。

---

计算流程图：

代码解析：
（刚写完突然格式一错啥也没了重来，以后要换地方了）
对应流程图最左边的部分，图卷积的模块：

## 建立模块1
class Encoder(nn.Module):
    def __init__(self, hidden_dim):
        super(Encoder, self).__init__()
        self.conv = GCNConv(dataset.num_features, hidden_dim)
        self.prelu = nn.PReLU(hidden_dim)

    def forward(self, x, edge_index, corrupt=False):
        if corrupt:
            perm = torch.randperm(data.num_nodes)
            x = x[perm]

        x = self.conv(x, edge_index)
        x = self.prelu(x)
        return x

对应图的右边部分，每一个图摘要summary对应了一个参数矩阵相乘，之后才与特征矩阵x做连乘：

## 建立模块2
class Discriminator(nn.Module):
    def __init__(self, hidden_dim):
        super(Discriminator, self).__init__()
        self.weight = nn.Parameter(torch.Tensor(hidden_dim, hidden_dim))
        self.reset_parameters()

    def reset_parameters(self):
        size = self.weight.size(0)
        uniform(size, self.weight)

    def forward(self, x, summary):
        x = torch.matmul(x, torch.matmul(self.weight, summary))
        return x

对应整个模型，nn.BCEWithLogitsLoss()对数据做sigmoid操作之后才计算二元交叉熵损失：
这里的torch.nn.BCEWithLogitsLoss(weight=None, size_average=None, reduce=None, reduction='mean', pos_weight=None)需要说一下：

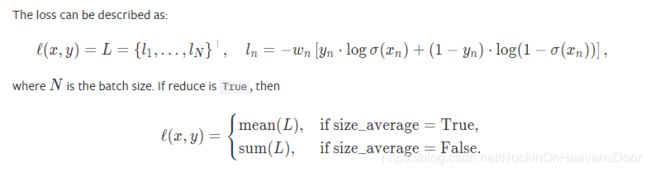
这里的size_average (bool, optional): Default: True,那么每个批样本数目作为分母得到整个$L$损失的均值作为最后的损失。
可以看到，每个样本出现的概率可以是不一样的，$p_n$对应着这样的一个正负样本比例的偏置。

## 根据模块1、模块2构建模型：1. 定义模块1、模块2的使用过程，2. 构造最终的损失函数

class Infomax(nn.Module):
    def __init__(self, hidden_dim):
        super(Infomax, self).__init__()
        self.encoder = Encoder(hidden_dim)
        self.discriminator = Discriminator(hidden_dim)
        self.loss = nn.BCEWithLogitsLoss()

    def forward(self, x, edge_index):
        positive = self.encoder(x, edge_index, corrupt=False)
        negative = self.encoder(x, edge_index, corrupt=True)
        # 隐层多少，summary就是多少大小
        summary = torch.sigmoid(positive.mean(dim=0))

        positive = self.discriminator(positive, summary)
        negative = self.discriminator(negative, summary)

        l1 = self.loss(positive, torch.ones_like(positive))
        l2 = self.loss(negative, torch.zeros_like(negative))

        return l1 + l2

---

• 我写的信息论的扩展：https://www.jianshu.com/p/e3d9ef4f3eae