数据分析--时间问题与降维
数据降维降低预测时间
使用自带的数字模型,查看使用KNN算法和逻辑回归算法的分类时间,并降低数据维度缩短预测时间
一般处理速度问题的几个方面
1. 数据量太大 (抽样)
2. 样本特征太多 (降维)
3. 样本的量级太大(归一化)
4. 算法本身的问题
一、查看KNN与lgc(逻辑回归)处理分类问题的时间
这里使用sklean自带的数据–图片数据类进行分类
1)导包
from sklearn.datasets import load_digits
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 2)获取数据并处理
digits = load_digits()
data = digits.data # 特征值
target = digits.target # 目标值3)查看图片数据
plt.imshow(data[0].reshape(8,8),cmap='gray')4)拆分数据
将数据拆分为训练集与测试机
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data,target)5)对比 knn 和 lgc逻辑回归 分类 的 时间
1、导包
from sklearn.neighbors import KNeighborsClassifier # KNN
from sklearn.linear_model import LogisticRegression # 逻辑回归2、获取模型
knn = KNeighborsClassifier() # KNN
lgc = LogisticRegression() # lgc3、模型训练
%time knn.fit(X_train,y_train)
Wall time: 5.96 msknn的训练是很快的 因为只是记录了一下各个点的位置
%time lgc.fit(X_train,y_train)
Wall time: 153 ms逻辑回归 在 训练的时候 是很慢的 因为要找规律
4、模型预测
%time knn.predict(X_test)
Wall time: 73.8 msknn在测试的时候 时间就比较长了 247 ms
%time lgc.predict(X_test) lgc在预测的时候就快了
二、数据降维 PCA 和LDA 原理
1)PCA:主成分分析
Principal Component Analysis
将本类数据的差异保存做最完整
对一类数据进行降维处理。
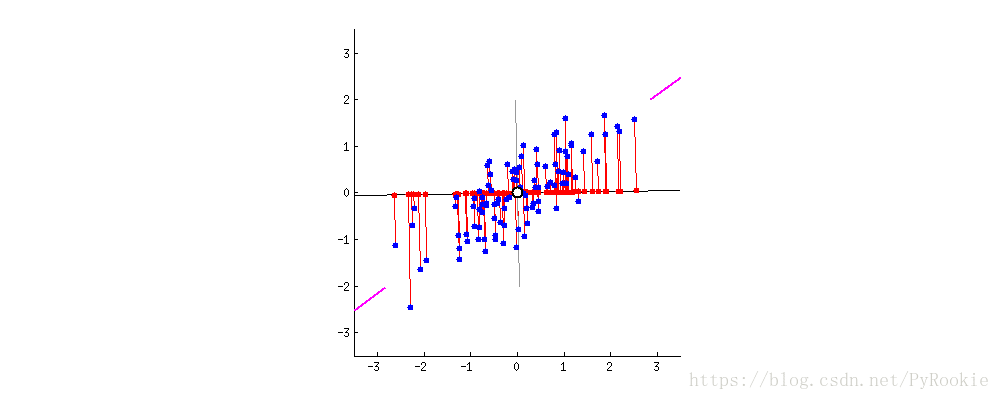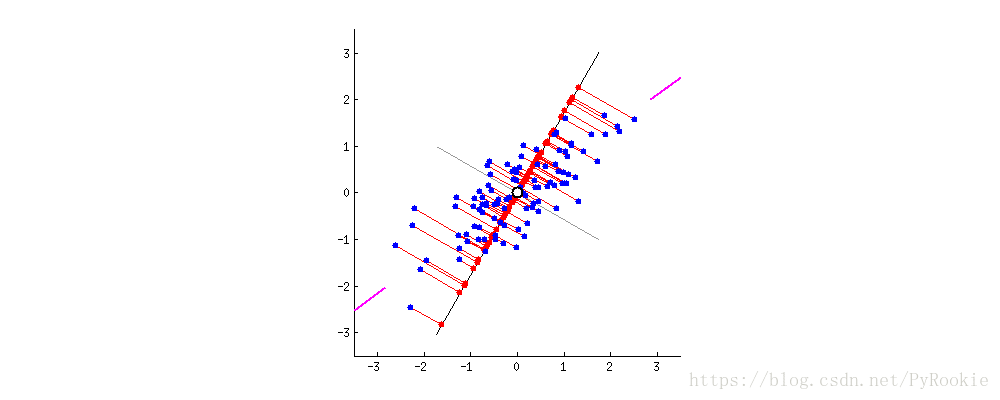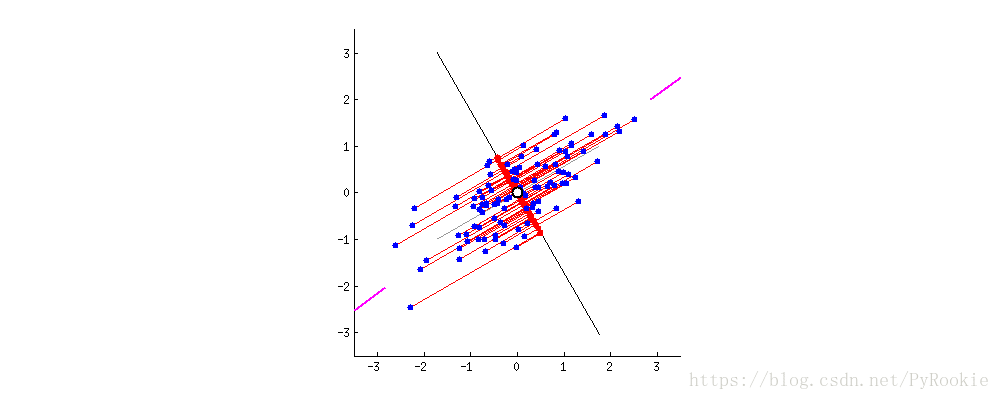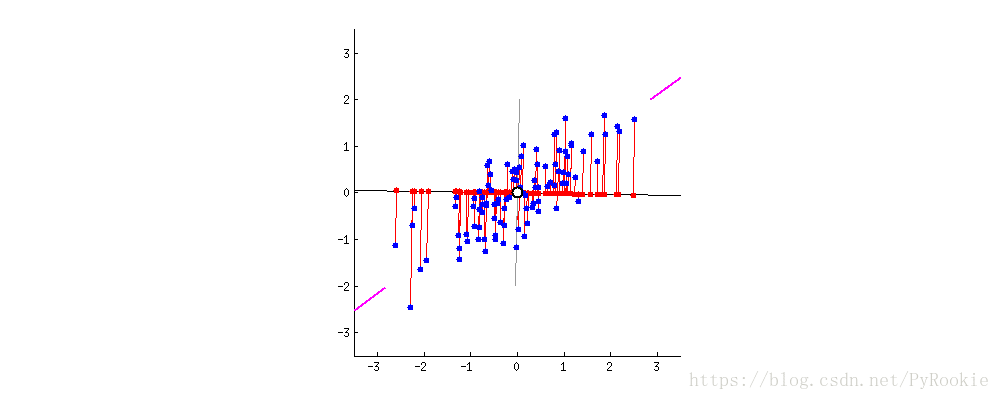
如图显示,将下面这些蓝色的点压缩到一条线上,但这条线为下面这个状态时,所取到的值最离散
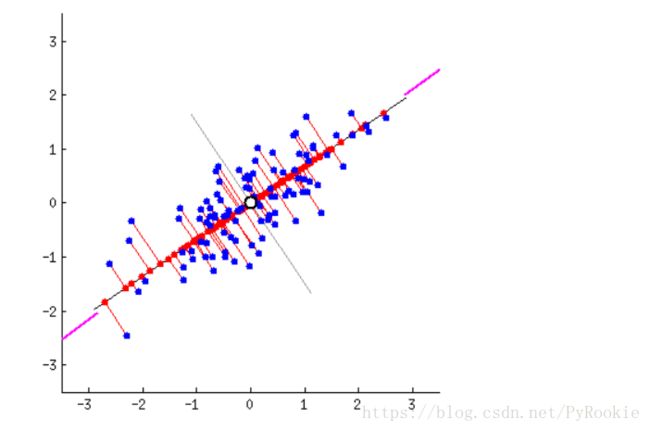
将蓝色的点这样压缩时的效果最不好,这些点都聚到一起了,不能区分开各个点。
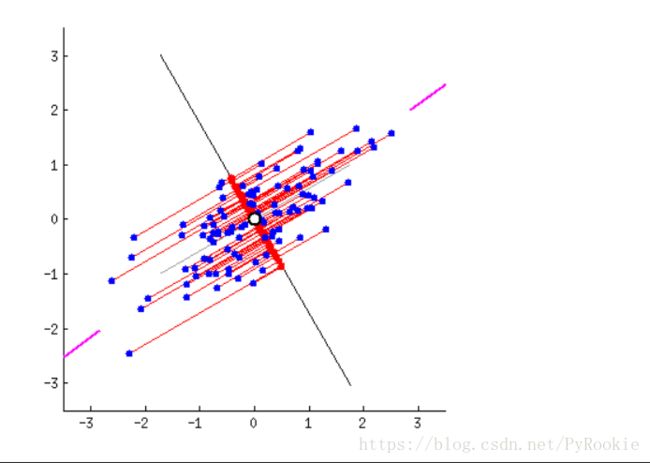
2)LDA:线性判别分析
参考两组之间的差异,保存连类之间的最大差异
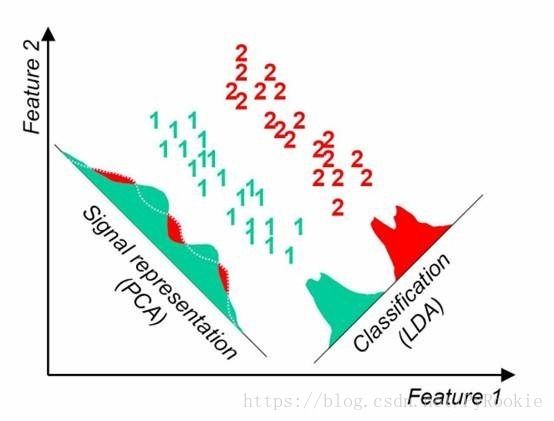
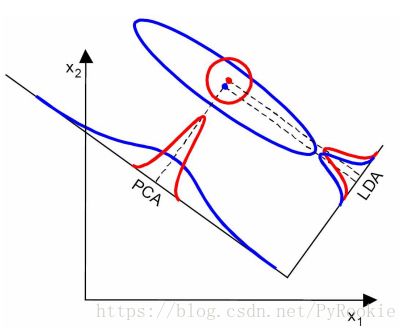
3)两种分类比较
三、数据降维
1)加载数据
这是一组图片数据
df = pd.read_csv('./data/digits.csv')
df.shape
(42000, 785) # 42000个样本, 785个 28*28的像素点2)数据处理
target = df['label'] # 目标值
data = df.iloc[:,1:] # 特征值查看图片内容
plt.imshow(data.iloc[0].values.reshape(28,28))切分训练集和数据集
X_train,X_test,y_train,y_test = train_test_split(data,target)3)使用KNN和lgc进行训练
1、KNN模型 训练数据
knn = KNeighborsClassifier()
%time knn.fit(X_train,y_train)
Wall time: 5.02 ms2、KNN模型 预测
%time y_ = knn.predict(X_test)
Wall time: 82.8 ms3、lgc模型 训练数据
lgc = LogisticRegression()
%time lgc.fit(X_train,y_train)
Wall time: 149 ms4、lgc模型 预测
%time lgc.predict(X_test)
Wall time: 0 ns4)使用PCA降维缩短时间
1、导包
from sklearn.decomposition import PCA2、训练集、测试集分离
X_train = data[:5000] # 前5000个作为测试数据
y_train = target[:5000]
X_test = data[-500:] # 最后500个作为训练数据
y_test = target[-500:]3、获取pca模型
pca = PCA(n_components=0.9)
# n_components 留下的部分(维度 特征)
# 这里的0.9不是 留下 90% 个特征4、训练pca模型
pca.fit(X_train)5、pca模型转换(降维)
pca_X_train = pca.transform(X_train)pca_X_train.shape
(5000, 85) #这里可以看到设置 为0.9降维之后剩下85个特征5)KNN预测使用pca降维后的测试集的准确率并和没有降维处理的比较
降维处理后的
knn = KNeighborsClassifier()
knn.fit(pca_X_train,y_train)
pca_X_test = pca.transform(X_test)
%time knn.score(pca_X_test,y_test)
Wall time: 1.13 s
0.94没有降维处理的
knn2 = KNeighborsClassifier()
knn2.fit(X_train,y_train)
%time knn2.score(X_test,y_test)
Wall time: 7.67 s
0.9326)lgc预测使用pca降维后的测试集的准确率并和没有降维处理的比较
降维处理后的
lgc = LogisticRegression()
%time lgc.fit(X_train,y_train)
Wall time: 1.39 s
knn.score(X_test,y_test)
Wall time: 998 µs
1.0没有降维处理的
lgc2 = LogisticRegression()
%time lgc2.fit(X_train,y_train)
Wall time: 1min 20s
knn2.score(X_test,y_test)
Wall time: 23.9 ms
0.9998四、鸢尾花数据降维
演示降维的效果 和对分类准确率的影响
1)导包
from sklearn.datasets import load_iris2)数据获取
iris = load_iris()
data = iris.data # 特征值
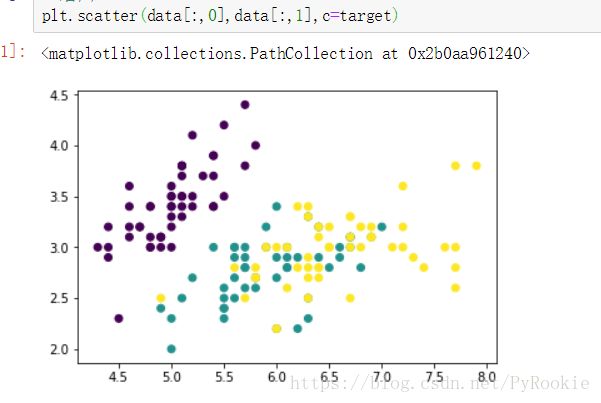
target = iris.target # 目标值降维之前 前两维度的效果
plt.scatter(data[:,0],data[:,1],c=target)3)切分数据集,查看降维前预测准确率
切分数据集,比较降维前后的数据准确率对比
1、切分数据集
from sklearn.neighbors import KNeighborsClassifier
X_train,X_test,y_train,y_test = train_test_split(data,target)2、KNN训练集训练,测试集预测
knn = KNeighborsClassifier()
knn.fit(X_train,y_train)
knn.score(X_test,y_test)
0.97368421052631583、交叉验证准确率
scores = [] # 创建一个空列表来接受预测数据
for i in [0.1,0.2,0.3]:
X_train,X_test,y_train,y_test = train_test_split(data,target,test_size=i) # 设置不同的训练集与数据集的切分比例
knn.fit(X_train,y_train)
score = knn.score(X_test,y_test)
scores.append(score) # 将不同的准确率加入到列表中
np.array(scores).mean() # 求各个切分比例的平均准确率
0.98148148148148154、定义函数查看模型预测准确率
def cross_verify(data,target,model):
scores = []
for i in [0.1,0.2,0.3]:
X_train,X_test,y_train,y_test = train_test_split(data,target,test_size=i)
model.fit(X_train,y_train)
score = model.score(X_test,y_test)
scores.append(score)
return np.array(scores).mean()5、使用lgc模型查看预测准确率
from sklearn.linear_model import LogisticRegression
cross_verify(data,target,KNeighborsClassifier())
0.9259259259259259五、PCA降维后查看准确率
1)导包
from sklearn.decomposition import PCA
# decomposition 分解2)降维模型获取
pca = PCA(n_components=2)
# n_components 传入整数:表示保留几个特征
传入小数:表示保留特征的比例3)降维模型训练
这里pca只需要特征值,不需要目标值
pca.fit(data)而lda 既需要特征值,也需要目标值,因为他需要知道那个特征是那个组的
4)模型转换
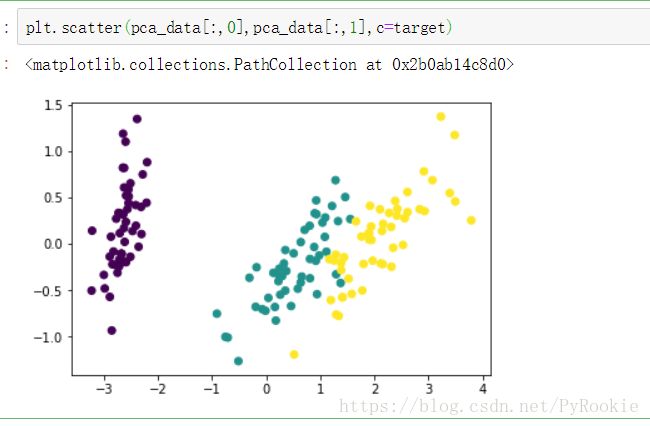
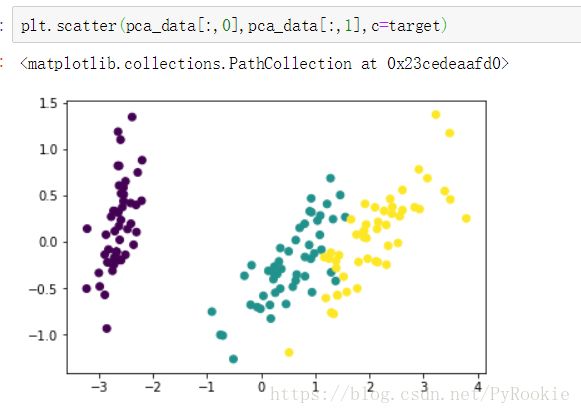
pca_data = pca.transform(data)5)使用转换后的数据进行绘图查看
plt.scatter(pca_data[:,0],pca_data[:,1],c=target)6)使用上面预测准确率的函数对pca降维后的数据进行测试
cross_verify(pca_data,target,KNeighborsClassifier())
0.9666666666666667可以看到降低了维度 准确率没有受到太大影响
7)使用LDA对鸢尾花数据进行降维
1、导包
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis2、获取模型
lda = LinearDiscriminantAnalysis(n_components=2)
# n_components 指定保留的维度3、训练模型
l da需要指定分组情况 才能找到各组直接中心距离最大的位置
lda.fit(data,target) 4、模型对数据转换
lda_data = lda.transform(data)查看lba转换后的数据
比较两者的x轴可观察出
lba找的是离中心点最远的点去绘制
pca找的是离中心点最近的去绘制
5、使用函数查看准确率
cross_verify(lda_data,target,KNeighborsClassifier())
0.99259259259259268)降维总结
总之 使用 降维算法 处理的数据 维度降低
如果数据量大 时间上会有明显提高
分类准确率并没有受到太大影响