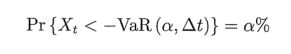Python-量化投资（一）

• 收益率=投资收益/投资成本
• 投资成=资产单价x资产数量
• 期间投资收益=期末价格-期初价格+其它收益
• 期间收益率=（期末价格-期初价格+其它收益）/期初价格
• 期间净收益率=（期末价格-期初价格+其它收益-卖出交易成本）/（期初价格+买入成本）

收益率

单期与多期

单期收益率：

import ffn
ffnSimpleret = ffn.to_returns(close)  #计算简单收益
ffnSimpleret.name="ffnSimpleret"
ffnSimpleret.head()

年化收益率：

#假定245个交易日
annualize =(1+dayret1).cumprod()[-1]**(245/311)-1
annualize  #通过某一天的收益，计算年华

#根据年月日季度计算收益

def annualizecom(returns,period):  #根据年月日季度计算收益
    if period == "day":
        annualize =(1+returns).cumprod()[-1]**(245/len(returns))-1
        return annualize
    elif period == "month":
        annualize =(1+returns).cumprod()[-1]**(12/len(returns))-1
        return annualize
    elif period == "quarter":
        annualize =(1+returns).cumprod()[-1]**(4/len(returns))-1
        return annualize
    elif period == "year":
        annualize =(1+returns).cumprod()[-1]**(1/len(returns))-1
        return annualize
    else:
        raise Exception("error")

单期连续复利收益率

lagclose =  close.shift(1) #偏移1行
comporet = np.log(close/lagclose)#计算指数收益
comporet.name="comporet"    #连续收益计算
comporet

多期连续复利收益率

comporet2 = np.log(close/close.shift(2))#计算指数收益
comporet2.name="comporet2"    #连续收益计算
comporet2

单期与多期连续复利收益率的关系

comporet=comporet.dropna()
sumcomporet = comporet + comporet.shift(1)
sumcomporet.plot()

资产风险

• 市场风险
• 利率风险
• 汇率风险
• 流动性风险
• 信用风险
• 通货膨胀风险
• 营运风险

资产风险的测度

• 方差（标准差）
  比较两个标准差的大小

returnS=ffn.to_returns(SAPower.Close).dropna()
returnD=ffn.to_returns(DalianRP.Close).dropna()
returnS.std()
returnD.std()

• 下行风险

def cal_half_dev(returns):  #下行风险
    mu=returns.mean()#平均值
    temp=returns[returns<mu]#小于平均值
    half_deviation = (sum((mu-temp)**2)/len(returns))**0.5
    return half_deviation

比较在收益均值之下的波动性

cal_half_dev(returnS)
cal_half_dev(returnD)

• 风险价值（VaR）
  数学表达式：
  

returnS.quantile(0.05)#历史模拟，下跌5%的概率
returnD.quantile(0.05)#历史模拟
from scipy.stats import norm           #历史数据评价下行风险
norm.ppf(0.05,returnS.mean(),returnS.std())  #协方差
norm.ppf(0.05,returnD.mean(),returnD.std()) 

代码	结果
returnS.quantile(0.05)	-0.043192456894806296
returnD.quantile(0.05)	-0.03408596308105866
norm.ppf(0.05,returnS.mean(),returnS.std())	-0.06621086216022148
norm.ppf(0.05,returnD.mean(),returnD.std())	-0.03274944602236822

历史模拟法的结果表明，returnS有5%的可能下跌超过4.319%，而returnD
有5%的可能下跌超过3.4085%。协方差矩阵法得到两个相似的结果。因此returnS的风险更大，这个结果与使用标准差、半离差得到的结果相一致。

• 期望亏空
  弥补VaR理论上的缺点

returnS[returnS<=returnS.quantile(0.05)].mean()
returnD[returnD<=returnD.quantile(0.05)].mean()

得到的理论结果和上述一致

• 最大回撤
  实务上经常用最大回撤（Maximun Drawdown，MDD）来衡量投资（特别是基金）的表现。最大回撤是指，某资产（或投资组合）在时刻T的回撤是指资产在（0，T）的最高峰值与现在价值Pt之间的回落值。

#模拟
import datetime
r=pd.Series([0,0.1,-0.1,-0.01,0.01,0.02],index=[datetime.date(2017,12,x) for x in range(3,9)])
value=(1+r).cumprod()#收益
D=value.cummax()-value  #差异
d = D/(D+value)
MDD = D.max()
mdd=d.max()
#验证
ffn.calc_max_drawdown(value) #最大回撤率
比，差距越大，风险越高

基于ffn包中的calc_max_drawdown（）函数来计算
实际代码：

ffn.calc_max_drawdown((1+returnS).cumprod())#最高峰的值与当下数据的对比，差距越大，风险越高
ffn.calc_max_drawdown((1+returnD).cumprod())

引用《量化投资以Python为工具 》