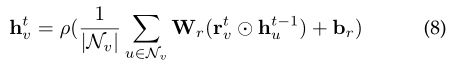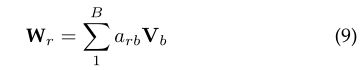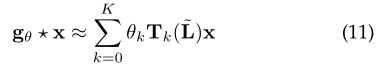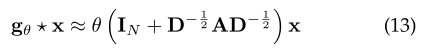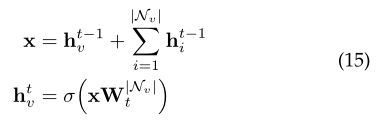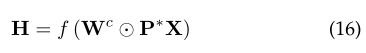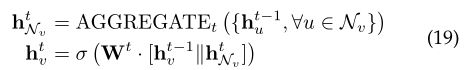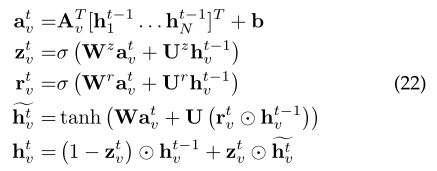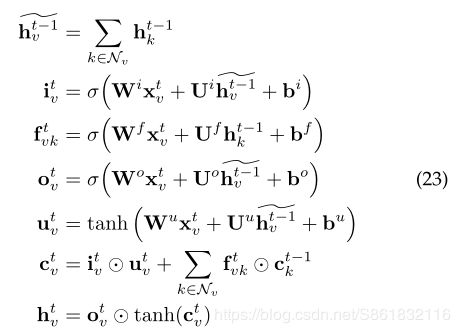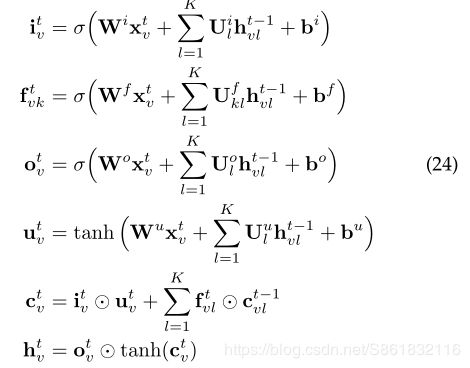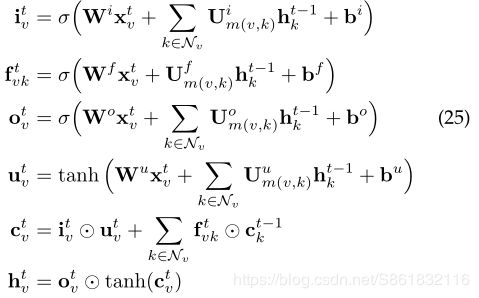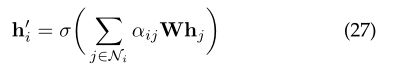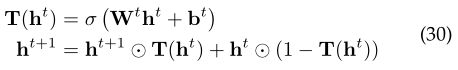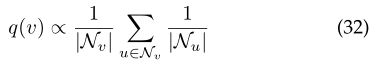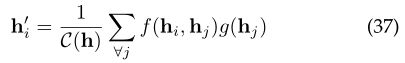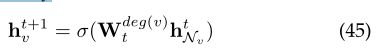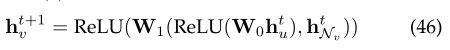Graph Neural Networks: A Review of Methods and Applications（图神经网络：方法与应用综述）

目录

摘要：

一.介绍

二.模型

2.1GNN

2.2图神经网络的变体

2.2.1Graph Types

2.2.3训练方法

2.3通用框架

2.3.1消息传递神经网络（Message Passing Neural Networks）

2.3.2非本地神经网络

2.3.3图网络

3.应用

3.1结构方案

3.1.1物理

3.1.2化学与生物

3.1.3知识图

3.2非结构性场景

3.2.1图像

3.2.2文本

3.3其他场景

3.3.1生成模型

3.3.2组合优化

4.开放的问题

5.结论

---

摘要：

许多学习任务需要处理图形数据，该图形数据包含元素之间的丰富关系信息。建模物理系统，学习分子指纹，预测蛋白质界面以及对疾病进行分类都需要一个模型来从图形输入中学习。在诸如从文本和图像之类的非结构数据中学习的其他领域中，对提取的结构的推理，例如句子的依存关系树和图像的场景图，是一个重要的研究课题，它也需要图推理模型。图神经网络（GNN）是连接器模型，可通过在图的节点之间传递消息来捕获图的依赖性。与标准神经网络不同，图神经网络保留了一种状态，该状态可以表示来自其邻域的任意深度的信息。尽管发现原始GNN难以在固定点上进行训练，但是网络体系结构，优化技术和并行计算的最新进展已使他们能够成功学习。近年来，基于图神经网络变体的系统，例如图卷积网络（GCN），图注意力网络（GAT），门控图神经网络（GGNN），已在上述许多任务上展现了突破性的性能。在本次调查中，我们对现有的图神经网络模型进行了详细的回顾，对应用程序进行了系统分类，并提出了四个未解决的问题，以供将来研究。

一.介绍

图形是一种数据结构，可对一组对象（节点）及其关系（边）进行建模（图形是对象和关系的建模）。近年来，由于图的强大表达能力，利用机器学习分析图的研究受到越来越多的关注，即图可以用作包括社会科学（社会网络）在内的各个领域的大量系统的表示[1]。]，[2]，自然科学（物理系统[3]，[4]和蛋白质-蛋白质相互作用网络[5]），知识图[6]和许多其他研究领域[7]。作为用于机器学习的独特的非欧氏数据结构，图分析着重于节点分类，链接预测和聚类。图神经网络（GNN）是在图域上运行的基于深度学习的方法。由于其令人信服的性能和高解释性，GNN最近已成为一种广泛应用的图形分析方法。在下面的段落中，我们将说明图神经网络的基本动机。

GNN的第一个动机源于卷积神经网络（CNN）[8]。CNN具有提取多尺度局部空间特征并将其组合以构建高度表达的表示的能力，这导致了几乎所有机器学习领域的突破，并开始了深度学习的新时代[9]。随着我们对CNN和图形的深入研究，我们发现了CNN的关键：本地连接，共享权重和多层[9]的使用。这些对于解决图域问题也非常重要，因为1）图是最典型的局部连接结构。2）与传统的谱图理论相比，共享权重降低了计算成本[10]。3）多层结构是处理分层模式的关键，它捕获了各种大小的特征。但是，CNN只能对诸如图像（2D网格）和文本（1D序列）之类的常规欧几里得数据进行操作，而这些数据结构可以视为图的实例。因此，直接考虑找到将CNN转换为图形的想法很简单。如图1所示，很难定义局部卷积滤波器和池化运算符，这阻碍了CNN从欧几里德域到非欧几里德域的转换。（目前的困难时CNN向非欧几里得域的转换）

图1.左:欧氏空间中的图像。右:非欧几里德空间中的图

另一个动机来自图嵌入[11] – [15]，它学会了在低维向量中表示图节点，边或子图。在图分析领域，传统的机器学习方法通​​常依赖于手工设计的功能，并且受其灵活性和高成本的限制。遵循表示学习的思想和词嵌入的成功[16]，DeepWalk [17]被认为是第一种基于表示学习的图嵌入方法，将SkipGram模型[16]应用于生成的随机游动。类似的方法，例如node2vec [18]，LINE [19]和TADW [20]也取得了突破。但是，这些方法有两个严重的缺点[12]。首先，编码器中的节点之间没有共享参数，这导致计算效率低下，因为这意味着参数的数量随节点的数量线性增长。其次，直接嵌入方法缺乏泛化能力，这意味着它们无法处理动态图或泛化为新图。

基于CNN和图嵌入，提出了图神经网络（GNN）来集合图结构中的信息。因此，他们可以对包含元素及其依存关系的输入和/或输出进行建模。此外，图神经网络可以使用RNN内核同时对图的扩散过程进行建模 。

在下面的部分中，我们解释了图神经网络值得研究的根本原因。首先，像（解释了为什么cnn和rnn不能正确处理图形的输入）CNN和RNN这样的标准神经网络无法正确处理图形输入，因为它们按特定顺序堆叠了节点的特征。但是，图中的节点没有自然顺序。为了完整地呈现图，我们应该遍历所有可能的阶数作为模型的输入，例如CNN和RNN，这在计算时非常多余。为了解决这个问题，GNN分别在每个节点上传播，而忽略节点的输入顺序。换句话说，GNN的输出对于节点的输入顺序是不变的（怎么输入的顺序就怎么输出顺序）。其次，图中的边表示两个节点之间的依存关系信息。在标准神经网络中，依赖信息仅被视为节点的特征（图结构中依赖信息更偏向于寄存在边上）。但是，GNN可以通过图结构进行传播，而不必将其用作特征的一部分。通常，GNN通过节点附近状态的加权总和来更新节点的隐藏状态。第三，推理是高级人工智能的一个非常重要的研究课题，人脑的推理过程几乎是基于从日常经验中提取的图。标准的神经网络已经显示出通过学习数据的分布来生成合成图像和文档的能力，而他们仍然无法从大型实验数据中学习推理图。但是，GNN试图从诸如场景图片和故事文档之类的非结构化数据生成图形，这可以成为进一步高级AI的强大神经模型。最近，已经证明，具有简单架构的未经训练的GNN效果也很好[21]（看效果） 。

关于图神经网络有一些全面的综述。[22]提出了一个统一的框架MoNet，将CNN架构泛化到非欧几里德域（图形和流形），并且该框架可以泛化图[2]，[23]上的几种频谱方法以及流形上的一些模型[24] ]，[25]。[26]对几何深度学习进行了全面的回顾，提出了它的问题，困难，解决方案，应用和未来方向。[22]和[26]专注于将卷积泛化为图或流形，但是在本文中，我们仅关注图上定义的问题，我们还研究了图神经网络中使用的其他机制，例如门机制，注意力机制和跳过连接。[27]提出了消息传递神经网络（MPNN），它可以推广几种图神经网络和图卷积网络的方法。[28]提出了一种非本地神经网络（NLNN），它统一了几种“自我注意”式的方法。但是，该模型未在原始论文的图形上明确定义。着眼于特定的应用领域，[27]和[28]仅给出了如何使用其框架来概括其他模型的示例，并且未提供对其他图神经网络模型的评论。[29]（要看）提供了对图注意力模型的综述。[30]提出了图网络（GN）框架，它具有很强的泛化其他模型的能力。然而，图网络模型是高度抽象的，[30]仅给出了应用的粗略分类。

[31]和[32]是有关GNN的最新调查论文，它们主要关注GNN模型。[32]将GNN分为五类：图卷积网络，图注意力网络，图自动编码器，图生成网络和图时空网络。我们的论文与[32]有不同的分类法。我们在第2.2.2节中介绍图卷积网络和图注意力网络，因为它们有助于传播步骤。我们在第2.2.1节中介绍图时空网络，因为模型通常用于动态图。我们在第2.2.3节中介绍图形自动编码器，因为它们是以无人监督的方式进行训练的。最后，我们在图生成的应用中介绍图生成网络（请参阅第3.3.1节）。

在本文中，我们对不同的图神经网络模型以及应用程序的系统分类学进行了全面的回顾。总而言之，本文对图神经网络进行了广泛的调查，并做出了以下贡献。

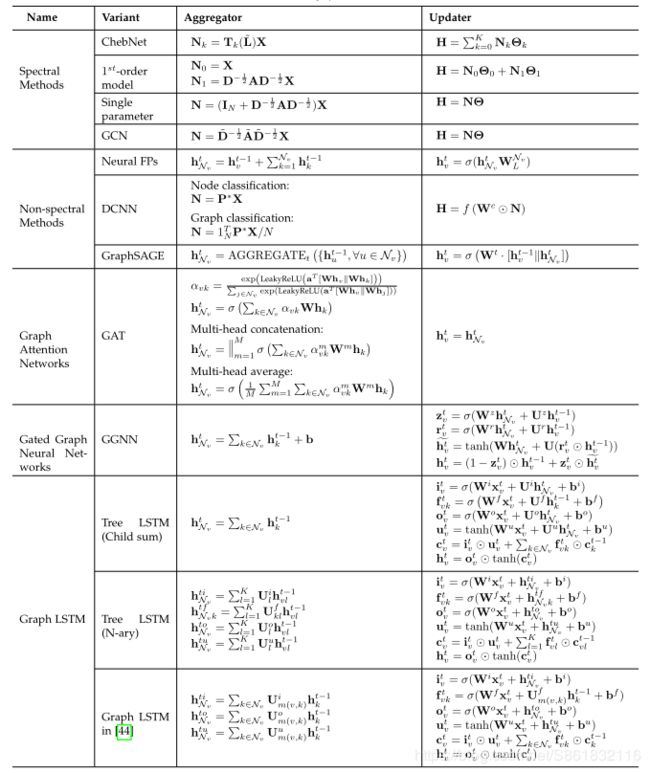
• 我们对现有的图神经网络模型进行了详细的回顾。我们介绍了原始模型，它的变体和几个通用框架。我们研究了该领域中的各种模型，并提供了统一的表示形式，以呈现不同模型中的不同传播步骤。通过识别相应的聚合器和更新器，可以使用我们的表示轻松区分不同的模型。
• 我们对应用程序进行系统地分类，并将应用程序分为结构方案，非结构方案和其他方案。针对每种情况，我们介绍几种主要的应用程序及其对应的方法。
• 我们提出了四个未解决的问题，以供将来研究。图神经网络存在过度平滑和缩放的问题。仍然没有有效的方法来处理动态图以及对非结构感官数据进行建模。我们将对每个问题进行详尽的分析，并提出未来的研究方向。

该调查的其余部分组织如下。在第2节中，我们介绍了图神经网络族中的各种模型。我们首先介绍原始框架及其局限性。然后，我们提出了它的变种，试图释放限制。最后，介绍了最近提出的几种通用框架。在第3节中，我们将介绍图神经网络在结构场景、非结构场景和其他场景中的几个主要应用。在第4节中，我们提出了图神经网络的四个开放问题以及未来的几个研究方向。最后，我们在第5节结束调查。

二.模型

图神经网络是非欧几里得结构上的有用工具，文献中提出了各种方法来尝试提高模型的功能。

在第2.1节中，我们描述了[33]中提出的原始图神经网络。我们还列出了原始GNN在表示能力和训练效率方面的局限性。在第2.2节中，我们引入了图神经网络的几种变体，旨在释放这些限制。这些变体在具有不同类型的图上运行，利用不同的传播函数和高级训练方法。在第2.3节中，我们提出了三个通用框架，它们可以概括和扩展几行工作。详细来说，消息传递神经网络（MPNN）[27]统一了各种图神经网络和图卷积网络方法。非局部神经网络（NLNN）[28]统一了几种“自我注意”式的方法。图网络（GN）[30]可以概括本文提到的几乎每个图神经网络变体。

在深入探讨各个部分之前，我们给出了将在本文中使用的符号。有关这些符号的详细说明，请参见表1。

2.1GNN

图神经网络（GNN）的概念最早在[33]中提出，它扩展了现有的神经网络，用于处理图域中表示的数据。在图中，每个节点自然是由其特征和相关节点定义的。GNN的目标是学习嵌入hv∈Rs的状态，其中包含每个节点的邻域信息。嵌入状态为节点v的s维向量，可用于生成输出Ov，例如节点标签。令f为参数函数，称为局部转移函数，该函数在所有节点之间共享，并根据输入邻域更新节点状态。并让g为描述输出产生方式的本地输出函数。然后，Hv和Ov被定义为

其中Xv，xco [v]，hne [v]，xne [v]分别是v的特征，其边缘的特征，状态以及v附近的节点的特征

令H，O，X和Xn为分别堆叠所有状态，所有输出，所有要素和所有节点要素构成的向量。然后我们有一个紧凑的形式

其中，F（全局转移函数）和G（全局输出函数）分别是图中所有节点的f和g的堆叠版本。H的值是等式的固定点。在图3中以F为收缩图唯一地定义。

在Banach不动点定理[34]的建议下，GNN使用以下经典迭代方案来计算状态：

式中，Ht表示H的第t次迭代。5迅速以指数形式收敛到方程式的解。对于任何初始值H（0）为3。注意，在f和g中描述的计算可以解释为前馈4神经网络。

当我们有了GNN的框架后，下一个问题是如何学习f和g的参数。有了监督的目标信息(特定节点的tv)，损失可以表示为:

其中p是受监管节点的数量。学习算法基于梯度下降策略，由以下步骤组成

• 状态由等式迭代更新。【1】直到时间T。它们逼近方程式的不动点解。【3】：H（T）≈H
• 权重的梯度W由损耗计算
• 权重W根据最后一步中计算出的梯度进行更新。

限制：尽管实验结果表明GNN是用于对结构数据进行建模的强大架构，但原始GNN仍然存在一些局限性。首先，针对固定点迭代更新节点的隐藏状态效率低下。如果放宽对不动点的假设，我们可以设计一个多层GNN以得到节点及其邻域的稳定表示。其次，GNN在迭代中使用相同的参数，而大多数流行的神经网络在不同的层中使用不同的参数，这是一种分层的特征提取方法。此外，节点隐藏状态的更新是一个顺序过程，可以受益于RNN内核（如GRU和LSTM）。第三，（边问题有待处理）边上还有一些信息性特征，这些特征无法在原始GNN中有效建模。例如，知识图中的边具有关系的类型，并且通过不同边传播的消息应根据其类型而有所不同。此外，如何学习边的隐藏状态也是一个重要的问题。最后，如果我们专注于节点的表示而不是图形，则不适合使用固定点，因为固定点上的表示分布将在值上更加平滑，并且对于区分每个节点的信息量较小。

                                                                             表1.本文使用的符号

2.2图神经网络的变体

在本小节中，我们介绍了图神经网络的几种变体。第2.2.1节着重于对不同图形类型进行操作的变量。这些变体扩展了原始模型的表示能力。第2.2.2节列出了对传播步骤的一些修改（卷积，门机制，注意机制和跳过连接），这些模型可以学习更高质量的表示。第2.2.3节介绍了使用高级训练方法的变量，这些方法可以提高训练效率。图2概述了图神经网络的不同变体。

2.2.1Graph Types（图变体）

在原始的GNN [33]中，输入图由带有标签信息和无向边的节点组成，这是最简单的图格式。但是，世界上有很多图变体。在本小节中，我们将介绍一些旨在对不同类型的图进行建模的方法。

有向图：图的第一个变体是有向图。可以视为两个有向边的无向边表明两个节点之间存在关系（一个无向边可以视为两个方向的有向边？？？）。但是，有向边比无向边可以带来更多的信息。例如，在知识图中，边从头实体开始，在头实体结束，头实体是尾实体的父类，这表明我们应该区别对待父类和子类的信息传播过程 。DGP [35]使用两种权重矩阵Wp和Wc来合并更精确的结构信息。传播规则如下所示：

其中分别为父母和孩子的归一化邻接矩阵。

异构体：图的第二个变体是异构图，其中存在多种类型的节点。处理异构图的最简单方法是将每个节点的类型转换为与原始特征连接的单特征向量。更重要的是，GraphInception [36]将元路径的概念引入了异构图的传播中。使用元路径，我们可以根据邻居的节点类型和距离对其进行分组。对于每个邻居组，GraphInception将其视为同构图中的子图进行传播，并将不同同构图的传播结果连接起来以进行集合节点表示。最近，[37]提出了一种利用节点级和语义级注意力的异构图注意力网络（HAN）。该模型具有同时考虑节点重要性和元路径的能力。

带有边信息的图：在图形的另一个变体中，每个边都有其他信息，例如边的权重或类型。我们列出了两种处理此类图的方法：首先，我们可以将图转换为二分图，其中原始边也变为节点，并且一个原始边被拆分为两个新边，这意味着边节点之间有两个新边。和开始/结束节点。G2S [38]的编码器对邻居使用以下聚合函数：

其中，Wr和br为不同类型的边（关系）传播参数。其次，我们可以针对不同类型的边上的传播采用不同的权重矩阵。当关系的数量很大时，r-GCN [39]引入了两种正则化以减少用于建模关系量的参数的数量：基础分解和块对角分解。通过基分解，每个Wris定义如下：

这里每个Wr是基数变换与系数arb的线性组合。在块对角分解中，r-GCN通过一组低维矩阵上的直接和定义每个Wr，与第一个矩阵相比，它需要更多的参数。

图2.图神经网络变体概述

动态图：图的另一个变体是动态图，它具有静态图结构和动态输入信号。为了捕获这两种信息，DCRNN [40]和STGCN [41]首先通过GNN收集空间信息，然后将输出馈送到序列模型，如序列到序列模型或CNN。不同的是，Structure-RNN [42]和ST-GCN [43]同时收集空间和时间消息。它们通过时间连接扩展了静态图结构，因此可以在扩展图上应用传统的GNN。

2.2.2传播种类

传播步骤和输出步骤在模型中获得节点（或边缘）的隐藏状态至关重要。正如我们在下面列出的那样，原始图神经网络模型在传播步骤中有几个主要修改，而研究人员通常在输出步骤中遵循简单的前馈神经网络设置。可以在表2中找到GNN不同变体的比较。这些变体利用不同的聚合器从每个节点的邻居和特定的更新程序收集信息，以更新节点的隐藏状态。

卷积：将卷积推广到图域的兴趣日益浓厚。在这个方向上的进展通常分为频谱方法和非频谱（空间）方法（卷积扩展到图域两大方向）。

光谱网络：【45】提出了频谱网络。通过计算图拉普拉斯算子的特征分解，在傅里叶域中定义卷积运算。可以将运算定义为信号x∈RN（每个节点的标量）与由θ∈RN参数化的滤波器gθ= diag（θ）的乘积： 

其中U是归一化图拉普拉斯算子的特征向量矩阵（D是图的度矩阵，A是图的邻接矩阵），其特征值Λ的对角矩阵。

该操作导致潜在的密集计算和非空间局部化的滤波器。[46]试图通过引入具有平滑系数的参数化来使频谱滤波器在空间上局部化。

ChebNet：[47]提出，可以用切比雪夫多项式Tk（x）直至kt的舍位展开来近似表示gθ（Λ）。因此，该操作为：

其中。λmax表示L的最大特征值。θ∈RK现在是Chebyshev系数的向量。Chebyshev多项式定义为Tk（x）= 2xTk-1（x）-Tk-2（x），其中T0（x）= 1和T1（x）= x。可以看出，由于该运算是Laplacian中的K阶多项式，因此它是K局部的。[48]提出了ChebNet。它使用这种K局部卷积来定义卷积神经网络，从而无需计算拉普拉斯算子的特征向量。

GCN：[2]将逐层卷积运算限制为K = 1，以缓解具有非常宽的节点度分布的图的局部邻域结构过拟合问题。它进一步接近λmax≈2和方程简化为：

具有两个自由参数的参数。在用约束参数的数量之后，我们可以得到以下表达式：

请注意，堆叠此运算符可能会导致数值不稳定性和梯度的爆炸/消失，[2]引入了重归一化技巧：，其中〜A =A + INand〜Dii ＝ Pj〜Aij。最后，[2]将定义概括为具有C个输入通道和F个特征图滤波器的信号X∈RN×C，如下所示：

其中是滤波器参数矩阵，而Z∈是卷积信号矩阵。

                                                            表2.图神经网络的不同变体

所有这些模型都使用原始图结构表示节点之间的关系。然而，在不同的节点之间可能存在隐式关系，因此提出了自适应图卷积网络（AGCN）来学习底层关系[49]。AGCN学习一个“残差”图拉普拉斯算子（应该是在49这篇论文有讲），并将其添加到原始拉普拉斯算子矩阵中。结果，它被证明在几个图结构化数据集中有效。

此外，[50]提出了一种基于高斯过程的贝叶斯方法（GGP），以解决半监督学习问题。它显示了模型与频谱滤波方法之间的相似之处，这可能会从另一个角度为我们提供一些见解。

但是，在上述所有光谱方法中，学习的滤波器取决于拉普拉斯特征根，而拉普拉斯特征根取决于图的结构，也就是说，在特定结构上训练的模型不能直接应用于具有不同结构的图。（上述光谱方法不能直接应用于具有不同结构的图）

非光谱方法（基于空间的方法）直接在图上定义卷积，并在空间上相邻的邻居上进行运算。非光谱方法的主要挑战是定义具有不同大小邻域的卷积运算并保持CNN的局部不变性。

神经FPs（缺点不能用于大规模的图）：[51]对不同度的节点使用不同的权值矩阵：

其中是第t层|Nv|次节点的权值矩阵，该方法的主要缺点是不能应用于节点度较多的大规模图。

DCNN：[23]提出了扩散-卷积神经网络(DCNNs)。转换矩阵用于定义DCNN中节点的邻域。对于节点分类，它有

其中X是输入要素的N×F张量（N是节点数，F是要素数）。P ∗是一个N×K×N张量，其中包含矩阵P的幂级数{P，P2，...，PK}。P是图邻接矩阵A的度归一化转换矩阵。每个实体都经过变换到一个扩散卷积表示，它是一个K×F矩阵，由F个特征上图扩散的K跳定义。然后将由K×F权重矩阵和非线性激活函数f定义。最后，H（N×K×F）表示图中每个节点的扩散表示。

至于图分类，DCNN只是取节点表示的平均值，

1N这里是一个N×1的矢量。DCNN也可以应用于边分类任务，这需要将边缘转换为节点并增加邻接矩阵。

DGCN：[52]提出了双图卷积网络（DGCN）来共同考虑图的局部一致性和全局一致性。它使用两个卷积网络来捕获局部/全局一致性，并采用无监督的损失对其进行集成。第一个卷积网络与等式相同。14.第二个网络将邻接矩阵与正点向互信息（PPMI）矩阵放置在一起：

其中Xp是PPMI矩阵，Dp是Xp的对角度矩阵。

PATCHY-SAN：PATCHY-SAN模型[53]为每个节点提取并归一化正好k个节点的邻域（让每个节点附近有固定个数的相邻接点）。然后归一化的邻域充当卷积运算的接受场。

LGCN：LGCN [54]还利用CNN作为聚合器。它对节点的邻域矩阵进行最大池化，以获取前k个要素元素，然后应用一维CNN来计算隐藏表示。

MoNet.[22]提出了一个非欧氏域上的空间域模型（MoNet），该模型可以推广几种先前的技术。流形上的测地线CNN（GCNN）[24]和各向异性CNN（ACNN）[25]或图形上的GCN [2]和DCNN [23]可以表示为MoNet的特定实例。

GraphSAGE.[1]提出了GraphSAGE，一个通用的归纳框架。该框架通过对节点本地邻居的特征进行采样和聚合来生成嵌入。

然而，[1]没有利用等式19中的全部邻居集合，而是通过统一采样来利用固定大小的邻居集合。[1]提出了三种聚合函数。

均值聚合器。可以将其视为转导性GCN框架中卷积运算的近似值[2]，因此可以通过以下方式导出GCN变体的归纳形式：

• 均值聚合器与其他聚合器不同，因为它不执行将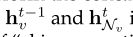等式19串联的串联操作。它可以看作是“跳过连接（跳过链接是什么？？）”的一种形式[55]，并且可以实现更好的性能。
• LSTM聚合器（被顺序处理所限制）.[1]还使用了基于LSTM的聚合器，该聚合器具有更大的表达能力。但是，LSTM按顺序处理输入，因此它们不是置换不变的。[1]通过置换节点的邻居使LSTM适应于无序集合。
• 池聚合器.在池聚合器中，每个邻居的隐藏状态通过完全连接的层馈送，然后将最大池操作应用于该节点的邻居集合。

注意，在这里可以使用任何对称函数代替最大池化操作。

最近，已经提出了结构感知卷积和StructureAware卷积神经网络[SACNN] [56]。单变量函数用作过滤器，它们可以处理欧氏和非欧氏结构化数据。

门：有几项工作试图在传播步骤中使用门机制，例如GRU [57]或LSTM [58]，以减少以前的GNN模型中的限制，并改善信息在整个图结构中的长期传播。

[59]提出了门控图神经网络（GGNN），该门网络在传播步骤中使用门递归单元（GRU），展开固定步数T的递归，并使用时间的反向传播来计算梯度。

具体来说，传播模型的基本递归是

节点v首先聚合来自其邻居的消息，其中Av是图邻接矩阵A的子矩阵，并表示节点v与它的邻居的连接。类似GRU的更新功能结合了来自其他节点和上一时间步的信息，以更新每个节点的隐藏状态。a收集节点v的邻域信息，z和r是更新和重置门。

在基于树或图的传播过程中，LSTM也以与GRU相似的方式使用。

[60]提出了对基本LSTM体系结构的两个扩展：Child-Sum T ree-LSTM和Nary T reeLSTM。像在标准LSTM单元中一样，每个Tree-LSTM单元（由v索引）都包含输入和输出门iv和ov，即存储单元cv和隐藏状态hv。Tree-LSTM单元包含一个遗忘门Fvk，而不是单个遗忘门，每个子k包含一个遗忘门fvk，从而使该单元可以选择性地合并每个子项的信息。子和树-LSTM转换方程式如下：

在标准的LSTM设置中，Xt是在t时刻的输入矢量。

如果一棵树的分支因子最多为K并且节点的所有子节点都已排序，即它们的索引号可以从1到K，则可以使用N元树LSTM。对于节点v，ht vk和ct vk分别表示在时间t第k个子节点的隐藏状态和存储单元。过渡方程如下：

与子和树LSTM相比，为每个子k引入单独的参数矩阵使模型可以学习更多关于单位子状态的细粒度表示。

两种类型的Tree-LSTM可以轻松地适应该图。[61]中的图结构LSTM是应用于该图的N元树LSTM的示例。但是，它是简化版本，因为图中的每个节点最多具有2个传入边（来自其父级和同级前辈）。[44]基于关系提取任务，提出了图LSTM的另一种变体。图和树之间的主要区别在于图的边缘具有标签。[44]利用不同的权重矩阵来表示不同的标签。

其中m（v，k）表示节点v和k之间的边标签。

[62]提出了用于改进文本编码的句子LSTM（S-LSTM）。它将文本转换为图形，并利用Graph LSTM学习表示形式。S-LSTM在许多NLP问题中显示出强大的表示能力。[63]提出了一个Graph LSTM网络来解决语义对象解析任务。它使用置信度驱动方案来自适应地选择起始节点并确定节点更新顺序。它遵循将现有LSTM概括为图结构化数据的相同想法，但是具有特定的更新顺序，而我们上面提到的方法与节点的顺序无关。

注意力：注意力机制已成功用于许多基于序列的任务，例如机器翻译[64] – [66]，机器阅读[67]等。[68]提出了一个图注意力网络（GAT），它将注意力机制纳入了传播步骤。它遵循自我注意策略，通过照看每个节点的邻居来计算每个节点的隐藏状态。

[68]定义了一个单一的图注意力层，并通过堆叠该层来构建任意图注意力网络。该层通过以下方式计算节点对（i，j）的注意力机制中的系数： 

其中αij是节点j对i的关注系数，Ni表示图中节点i的邻域。该层的节点要素的输入集为h = {h1，h2，。。。。，hN}，hi∈RF，其中N是节点数，F是每个节点的要素数，该层会生成一组新的节点要素（可能具有不同的基数F0），h0 = {h0 1，h02 ，。。。,, h0 N}，h0i∈RF0，作为其输出。W∈RF0×F是应用于每个节点的共享线性变换的权矩阵，a∈R2F0是单层前馈神经网络的权向量。通过softmax函数对其进行归一化，并应用LeakyReLU非线性（负输入斜率α= 0.2）。

然后，可以通过（在应用非线性σ之后）获得每个节点的最终输出特征：

此外，该层类似于[66]利用多头注意力来稳定学习过程。它应用K个独立的注意机制来计算隐藏状态，然后将其特征连接起来（或计算平均值），从而得到以下两种输出表示形式：

其中αkij是通过第k个注意力机制计算的归一化注意力系数。

文献[68]中的注意力体系结构具有几个特性：（1）节点-邻居对的计算是可并行的，因此操作是有效的；（2）通过为邻居指定任意权重，可以应用于不同程度的图节点；（3）它可以轻松地应用于归纳学习问题。

除了GAT，门控注意力网络（GAAN）[69]还使用了多头注意力机制。但是，它使用一种自我关注机制来收集来自不同负责人的信息，以代替GAT的平均操作。

跳跃连接：许多应用程序会展开或堆叠图神经网络层，以期获得更好的结果，因为更多的层（即k层）使每个节点从k跳处的邻居中收集更多信息。但是，在许多实验中都发现，更深层的模型无法改善性能，而更深层的模型甚至可能表现更差[2]。这主要是因为更多的层也可以从成倍增加的扩展邻域成员中传播噪声信息。

可以从计算机视觉社区找到一种简单的方法来解决该问题，即剩余网络[70]。但是，即使存在残留连接，具有更多层的GCN在许多数据集上的性能也不如2层GCN [2]。（层数越多性能反而越差）

[71]提出了一种高速公路GCN（性能在4层达到峰值，而不是两层），它使用类似于高速公路网络[72]的分层门。图层的输出与其输入的选通权重相加：

通过增加高速公路的闸门，在[71]中讨论的特定问题中，性能会在4层达到峰值。在[73]中提出的列网络（CLN）也利用了高速公路网络。但是它具有不同的功能来计算门控权重。

[74]研究性质和邻域聚合方案的结果限制。它提出了一个跳跃知识网络（可以根据需要调整每个节点的有效邻域大小），该网络可以学习自适应的结构感知表示（？？？）。Jump Knowledge Network从最后一层的每个节点的所有中间表示（“跳到最后一层”）中选择一个，这使模型可以根据需要调整每个节点的有效邻域大小。[74]在实验中使用了串联，最大池化和LSTM注意三种方法来汇总信息。跳跃知识网络在社交，生物信息学和引文网络的实验中表现出色。它也可以与诸如图卷积网络，GraphSAGE和图注意力网络之类的模型结合以提高其性能。

分层池（Hierarchical Pooling.）：在计算机视觉领域，卷积层通常后面是池化层，以获取更一般的功能。与这些池化层相似，许多工作都集中在设计图上的分层池化层上。复杂的大型图通常带有丰富的层次结构，这对于节点级和图级分类任务非常重要。

为了探究这种内部特征（分层池化层这种内部特征），边条件卷积（ECC）[75]设计了具有递归下采样操作的池化模块。下采样方法基于通过拉普拉斯算子的最大特征向量的符号将图分为两个分量的方法。

扩散池（DIFFPOOL）：[76]提出了一种可学习的层次聚类模块，在每一层训练一个赋值矩阵:

其中X（l）是节点特征，而A（l）是l层的粗化邻接矩阵。（这里面的（l）都是右上标）.

2.2.3训练方法

原始的图卷积神经网络在训练和优化方法上有几个缺点（对于大型图计算量巨大，并缺乏归纳学习能力.

）。具体来说，GCN需要完整的图拉普拉斯算子，这对于大型图来说是计算量巨大的事情。此外，通过在L-1层的所有邻居的嵌入来递归计算在L层的节点的嵌入。因此，单个节点的接收场相对于层数呈指数增长，因此计算单个节点的梯度会花费很多。最后，对GCN进行独立训练以获取固定图，该图缺乏归纳学习的能力。

抽样.GraphSAGE [1]是原始GCN的全面改进。为了解决上述问题，GraphSAGE用可学习的聚合函数替换了完整的图拉普拉斯算子，这是执行消息传递和泛化到看不见的节点的关键。如式19所示，它们首先聚合邻域嵌入，与目标节点的嵌入连接，然后传播到下一层。通过学习的聚合和传播功能，GraphSAGE可以为看不见的节点生成嵌入。此外，GraphSAGE使用邻居采样来减轻接收场扩展。

（PinSage和FastGCN都是对Graph的进一步改进）PinSage [77]提出了基于重要性的抽样方法。通过模拟从目标节点开始的随机游走，此方法选择了标准化访问次数最高的前T个节点。

FastGCN [78]进一步改进了采样算法。FastGCN不会为每个节点采样邻居，而是直接为每个层采样接收场。FastGCN使用重要性抽样，其重要性因子计算如下： 

与上面的固定采样方法相反，[79]引入了一个参数化且可训练的采样器来执行以前一层为条件的逐层采样。此外，该自适应采样器可以找到最佳采样重要性并同时减少方差。

在加强学习之后，SSE [80]提出了用于GNN训练的随机不动点梯度下降。此方法将嵌入更新视为值函数，将参数更新视为值函数。在训练期间，该算法将对节点进行采样以更新嵌入，并对标记的节点进行采样以交替更新参数。

接受域控制（Receptive Field Control）：[81]通过利用节点的历史激活作为控制变量，提出了一种基于控制变量的GCN随机近似算法。该方法限制了1hop邻域中的接收场，但使用历史隐性状态作为负担得起的近似值。

数据扩充：[82]集中于GCN的局限性，其中包括GCN需要许多附加的标记数据进行验证，并且还存在卷积滤波器的局部性。为了解决这些限制，作者提出了联合训练GCN和自训练GCN来扩大训练数据集。前一种方法查找训练数据的最近邻居，而后一种方法遵循类似Boosting的方法。

无监督培训：GNN通常用于有监督或半监督学习问题。近来，存在将自动编码器（AE）扩展到图域的趋势。图自动编码器旨在通过无监督的训练方式将节点表示为低维向量。

图自动编码器（GAE）[83]首先使用GCN对图中的节点进行编码。然后，它使用简单的解码器重构邻接矩阵，并根据原始邻接矩阵与重构矩阵之间的相似度来计算损失（重构后和原来的差距）。

[83]也以变化的方式训练GAE模型，该模型被称为变化图自动编码器（VGAE）。此外，伯格等。在推荐系统中使用GAE，并提出了图形卷积矩阵完成模型（GC-MC）[84]，其性能优于MovieLens数据集上的其他基线模型。

对抗性正则化图形自动编码器（ARGA）[85]使用生成对抗性网络（GAN）来正则化基于GCN的图形自动编码器以遵循先前的分布。也有几种图形自动编码器，例如NetRA [86]，DNGR [87]，SDNE [88]和DRNE [89]，但是它们在框架中没有使用GNN。

2.3通用框架

除了图神经网络的不同变体之外，还提出了几种通用框架，旨在将不同的模型集成到一个框架中。[27]提出了消息传递神经网络（MPNN），它统一了各种图神经网络和图卷积网络方法。[28]提出了非局部神经网络（NLNN）。它统一了几种“自我注意”式的方法[66]，[68]，[90]。[30]提出了一种图形网络（GN），该网络统一了MPNN和NLNN方法以及许多其他变体，例如交互网络[4]，[91]，神经物理引擎[92]，CommNet [93]，structure2vec [7]，[94]，GGNN [59]，关系网络[95]，[96]，深度集[97]和点网[98]。

2.3.1消息传递神经网络（Message Passing Neural Networks）

[27]提出了一种在图上进行监督学习的通用框架，称为消息传递神经网络（MPNN）。MPNN框架抽象了几种最流行的图结构数据模型之间的共性，例如图卷积，门控图神经网络[45] [2]，[48]和非图谱[51]等。59]，交互网络[4]，分子图卷积[99]，深张量神经网络[100]等。

该模型包含两个阶段，消息传递阶段和读出阶段。消息传递阶段（即传播步骤）运行T个时间步长，并根据消息函数Mt和顶点更新函数Ut进行定义。使用消息mt v，隐藏状态的更新功能如下：

表示从节点v到w的边缘特征。读取阶段使用读取函数R根据以下公式计算整个图的特征向量： 

其中T表示总时间步长。消息功能Mt，顶点更新功能Ut和读出功能R可以具有不同的设置。因此，MPNN框架可以通过不同的功能设置来概括几种不同的模型。在这里，我们给出了推广GGNN的示例，其他模型的功能设置可以在[27]中找到。GGNN的功能设置为： 

其中为邻接矩阵，每个边缘标签为e。GRU是[57]中介绍的门控循环单元。i和j是函数R中的神经网络。

2.3.2非本地神经网络

[28]提出了非本地神经网络（NLNN）来捕获深度神经网络的长期依赖。非局部运算是计算机视觉中经典非局部均值运算的一种概括[101]。非本地操作将某个位置的响应计算为所有位置的特征的加权总和。位置集可以在空间，时间或时空中。因此，NLNN可以看作是不同的“自我关注”式方法的统一[66]，[68]，[90]。我们将首先介绍非本地操作的一般定义，然后介绍一些特定的实例。

在非局部均值运算[101]之后，通用非局部运算定义为：

其中，i是输出位置的索引，j是枚举所有可能位置的索引。f（hi，hj）计算i和j之间的标量，表示它们之间的关系。g（hj）表示输入hj的变换，因子用于归一化结果。

有几个具有不同的f和g设置的实例化。为简单起见，[28]使用线性变换作为函数g。这意味着g（hj）= Wghj，其中Wg是一个学习的权重矩阵。接下来，我们在下面列出函数f的选择。

高斯：高斯函数是根据非局部均值[101]和双边滤波器[102]的自然选择。从而：

此处，是点积相似度，并且C（h）= 。

嵌入式高斯：通过计算嵌入空间中的相似度来扩展高斯函数很简单，这意味着：

可以发现[66]中提出的自我注意是嵌入式高斯模型的特例。对于给定的i，沿维度j成为softmax计算。因此，h丿 = ，与[66]中的自注意力形式相匹配。

点积：函数f也可以实现为点积相似性：

在这里，系数C（h）= N，其中N是h中的位置数。

串联：有公式

其中wf是将向量投影到标量的权重向量，而C（h）= N。

[28]将上述非本地操作包装到一个非本地块中，如下所示：

其中在等式37中给出，“ + hi”表示残余连接[70]。因此，可以将非本地块插入任何预先训练的模型中，从而使该块更适用

2.3.3图网络

[30]提出了一种图网络（GN）框架，该框架概括并扩展了各种图神经网络，MPNN和NLNN方法[27]，[28]，[33]。我们首先在[30]中介绍图形定义，然后描述GN块，GN核心计算单元及其计算步骤，最后介绍其基本设计原理。

图的定义：在[30]中，图形定义为3元组G =（u，H，E）（此处为了表示法的一致性，我们使用H而不是V）。u是全局属性，H = {hi} i = 1：Nv是（基数为Nv的）节点集合，其中每个hiis是节点的属性。E = {（ek，rk，sk）} k = 1：Ne是边缘集（基数Ne），其中每个ek是边缘的属性，rk是接收者节点的索引，而忽略发送者节点的索引。

GN块：GN块包含三个“更新”功能φ和三个“聚合”功能ρ，

ρ函数必须对其输入的排列保持不变，并且应采用可变数量的参数。

计算步骤：GN块的计算步骤如下

1. 使用参数（ek，hrk，hsk，u）对每个边缘应用φe，并返回e0 k。每个节点i的结果每个边缘输出的集合为E0 i = {（e0 k，rk，sk）} rk = i，k = 1：Ne。并且E0 = S iE0 i = {（e0 k，rk，sk）} k = 1：Ne是所有边沿输出的集合。
2. ρe→h应用于，并将投影到顶点i的边的边更新汇总为e0 i，将在下一步的节点更新中使用。
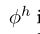3. 将应用于每个节点i，以计算更新的节点属性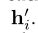。所得的每个节点输出的集合为。
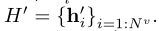4. ρe→u应用于E丿，并将所有边缘更新汇总到E丿中，然后将其用于下一步的全局更新中。
5. ρh→u应用于H丿，并将所有节点更新汇总为，然后将其用于下一步的全局更新。
6. 每个图应用一次，并计算全局属性u丿的更新。

请注意，这里的命令不是严格执行的。例如，可以从全局到每个节点进行持久更新。φ和ρ函数不必是神经网络，尽管在本文中我们仅关注神经网络的实现。

设计原则：基于三个基本原理的图网络设计：灵活的表示，可配置的块内结构和可组合的多块体系结构。

灵活的表示：GN框架支持属性的灵活表示以及不同的图结构。全局，节点和边属性可以使用任意表示形式，但是实值向量和张量是最常见的。可以根据任务的特定需求简单地定制GN块的输出。例如，[30]列出了几个边缘集中的[103]，[104]，节点集中的[3]，[4]，[92]，[105]和图形集中的[4]，[27]，[96] GN。就图结构而言，该框架既可以应用于图结构是显式的结构方案，也可以应用于应该推断或假定关系结构的非结构方案。

可配置的块内结构：GN块中的功能及其输入可以具有不同的设置，以便GN框架在块内结构配置中提供灵活性。例如，[104]和[3]使用完整的GN块。它们的φ实现使用神经网络，而ρ函数使用元素求和。基于不同的结构和功能设置，GN框架可以表示各种模型（例如MPNN，NLNN和其他变体）。更详细的信息可以在[30]中找到。

可组合多个块结构：GN块可以组成复杂的体系结构。GN块的任意数量可以按顺序共享或不共享。[30]利用GN块来构建编码过程-解码架构和基于GN的递归架构。这些架构在图3中进行了演示。用于构建基于GN的架构的其他技术也可能有用，例如跳过连接，LSTM或GRU风格的选通方案等。

3.应用

图神经网络已在跨监督，半监督，无监督和强化学习设置的广泛问题域中进行了探索。在本节中，我们将应用程序简单地划分为三种情况：（1）数据具有明确关系结构的结构性情况，例如物理系统，分子结构和知识图；（2）关系结构不明确的非结构场景包括图像，文字等；（3）其他应用场景，例如生成模型和组合优化问题。请注意，我们仅列出了几个代表性的应用程序，而没有提供详尽的列表。表3中列出了这些应用程序的摘要。

3.1结构方案（结构已知）

在以下小节中，我们将介绍GNN在结构化场景中的应用，在这种情况下，数据自然是在图形结构中执行的。例如，GNN被广泛用于社交网络预测[1]，[2]，流量预测[71]，[144]，推荐系统[77]（以后要看），[84]和图形表示[76]。具体来说，我们正在讨论如何使用对象关系图对现实世界的物理系统建模，如何预测分子的化学特性和蛋白质的生物相互作用特性以及知识中知识外碱基（OOKB）实体的推理方法图。

3.1.1物理

对现实世界的物理系统进行建模是了解人类智能的最基本方面之一。通过将对象表示为节点，将关系表示为边，我们可以以一种简单但有效的方式对对象，关系和物理进行基于GNN的推理。

[4]提出了交互网络来对各种物理系统进行预测和推断。该模型将对象和关系作为输入，相互作用的原因，并将效果和物理动力学应用于预测新状态。他们分别对以关系为中心和以对象为中心的模型进行建模，从而更容易在不同系统之间进行概括。在CommNet [93]中，没有明确建模交互。取而代之的是，通过平均所有其他代理的隐藏矢量来获得交互矢量。VAIN [90]进一步将注意方法引入到代理交互过程中，该方法同时保留了复杂性优势和计算效率。

视觉互动网络[91]可以根据像素做出预测。它从每个对象的两个连续输入帧中学习状态代码。然后，在通过互动网络模块添加互动效果后，状态解码器会将状态代码转换为下一步的状态。

[3]提出了一种基于图网络的模型，该模型可以执行状态预测或归纳推理。推理模型将部分观察到的信息作为输入，并构造一个用于隐式系统分类的隐藏图。

3.1.2化学与生物

分子指纹：计算分子指纹，这意味着代表分子的特征向量，是计算机辅助药物设计的核心步骤。传统的分子指纹是手工制作和固定的。通过将GNN应用于分子图，我们可以获得更好的指纹。

[51]提出了神经图指纹，该指纹通过GCN计算子结构特征向量并求和以获得整体表示。聚合函数是

euv是边（u，v）的边特征。然后通过更新节点表示

其中deg（v）是节点的度，是每个时间步长t和节点度N的学习矩阵。

[99]进一步明确地独立地对原子和原子对建模，以强调原子的相互作用。它介绍了聚集功能的边缘表示等。
。节点更新功能是 

                                                                               表3 图神经网络的应用

左：顺序GN块 中：编码处理解码 右：复发性GN块

                         图3.由GN块组成的体系结构示例。（a）顺序处理架构；（b）编码处理解码架构；（c）循环架构。

图4.应用场景

 

边更新函数为：

蛋白质界面预测：[5]专注于名为蛋白质界面预测的任务，这在药物发现和设计中的重要应用中是一个具有挑战性的问题。所提出的基于GCN的方法分别学习配体和受体蛋白残基表示并将其合并以成对分类。

GNN也可以用于生物医学工程。利用蛋白质-蛋白质相互作用网络，[135]利用图卷积和关系网络进行乳腺癌亚型分类。[134]也提出了基于GCN的多药房副作用预测模型。他们的工作为药物和蛋白质相互作用网络建模，并分别处理不同类型的边缘。

3.1.3知识图

[6]利用GNN解决知识库完成（KBC）中的知识库外（OOKB）实体问题。文献[6]中的OOKB实体直接连接到现有实体，因此OOKB实体的嵌入可以从现有实体中聚合。该方法在标准KBC设置和OOKB设置中均达到令人满意的性能。

[136]利用GCN来解决跨语言知识图对齐问题。该模型将来自不同语言的实体嵌入到统一的嵌入空间中，并根据嵌入相似性将它们对齐。

3.2非结构性场景

在本节中，我们将讨论非结构性场景下的应用程序，例如图像，文本，编程源代码[59]，[145]和多主体系统[90]，[93]，[103]。由于长度限制，我们仅对前两种情况进行详细介绍。粗略地讲，有两种方法可以将图神经网络应用于非结构场景：（1）结合其他领域的结构信息以提高性能，例如，使用知识图中的信息来减轻图像任务中的零射问题。（2）推断或假设场景中的关系结构，然后应用该模型解决在图形上定义的问题，例如[62]中将文本建模为图形的方法。

3.2.1图像

图分类：图像分类是计算机视觉领域的一项非常基础和重要的任务，它引起了广泛的关注，并拥有许多著名的数据集，如ImageNet [146]。图像分类的最新进展得益于大数据和GPU计算的强大功能，这使我们能够训练分类器而无需​​从图像中提取结构信息。但是，零镜头和少镜头学习在图像分类领域变得越来越普遍，因为大多数模型可以在有足够数据的情况下达到类似的性能。有许多利用图神经网络将结构信息纳入图像分类的工作。首先，知识图可以用作指导零短路识别分类的额外信息[35]，[121]。[121]建立了一个知识图，其中每个节点对应于一个对象类别，并以节点的词嵌入作为输入来预测不同类别的分类器。随着深度平滑的卷积结构发生过度平滑效应，[121]中使用的6层GCN将在表示中洗掉很多有用的信息。为了解决GCN传播中的平滑问题，[35]设法使用具有较大邻域的单层GCN，该邻域在图中既包含一跳节点也包含多跳节点。事实证明，它可以有效地与现有分类器建立零射流分类器。

除了知识图之外，数据集中图像之间的相似性也有助于几次学习[120]。[120]提出基于相似度建立加权全连接图像网络，并在图中传递消息以进行几次镜头识别。由于大多数知识图的推理能力很大，因此[123]根据对象检测的结果选择一些相关实体来构建子图，并将GGNN应用于提取的图进行预测。此外，[122]提出构造一个新的知识图，其中实体都是类别。并且，他们定义了三种标签关系类型：超从属，正相关和负相关，并直接在图中传播标签的置信度。

视觉推理：计算机视觉系统通常需要通过合并空间和语义信息来执行推理。因此为推理任务生成图很自然。

一个典型的视觉推理任务是视觉问答（VQA），[124]分别构造图像场景图和问题句法图。然后将其应用于GGNN训练嵌入以预测最终答案。尽管对象之间存在空间联系，但[147]建立了以问题为条件的关系图。利用知识图，[119]，[125]可以执行更好的关系探索和更可解释的推理过程。

视觉推理的其他应用包括对象检测，交互检测和区域分类。在对象检测[126]，[127]中，GNN用于计算RoI特征；在交互检测[42]，[128]中，GNN是人与物之间的消息传递工具。在区域分类[129]中，GNN对连接区域和类别的图执行推理。

语义分割：语义分割是迈向图像理解的关键步骤。此处的任务是为图像中的每个像素分配一个唯一的标签（或类别），这可以视为密集的分类问题。但是，图像中的区域通常不是网格状的，并且需要非本地信息，这导致了传统CNN的失败。一些作品利用图结构数据来处理它。

[63]提出了Graph-LSTM，通过建立基于距离的超像素图形式的图并应用LSTM在全球范围内传播邻域信息来对长期依赖关系和空间连接进行建模。随后的工作从编码分层信息的角度对其进行了改进[130]。

此外，3D语义分割（RGBD语义分割）和点云分类利用更多的几何信息，因此很难通过2D CNN进行建模。[133]构造了一个K最近邻（KNN）图，并使用3D GNN作为传播模型。展开几个步骤后，预测模型将每个节点的隐藏状态作为输入并预测其语义标签。

由于总是有太多的点，[131]通过构建超点图并为其生成嵌入来解决大规模3D点云分割。为了对超节点进行分类，[131]利用了GGNN和图卷积。

[132]提出通过边缘对点的相互作用进行建模。他们通过输入其末端节点的坐标来计算边缘表示向量。然后，通过边缘聚合来更新节点嵌入。

3.2.2文本

图神经网络可以应用于基于文本的多个任务。它可以应用于句子级任务（例如文本分类）以及词级任务（例如 序列标签）。下面，我们将介绍几个主要的文本应用程序。

文本分类：文本分类是自然语言处理中的一个重要而经典的问题。经典的GCN模型[1]，[2]，[22]，[23]，[46]，[48]和GAT模型[68]用于解决该问题，但它们仅使用文档之间的结构信息而且他们不使用太多文字信息。[106]提出了一种基于graphCNN的深度学习模型，该模型首先将文本转换为单词图，然后在[53]中使用图卷积运算对单词图进行卷积。[62]提出了句子LSTM对文本进行编码。它将整个句子视为一个状态，包括单个单词的子状态和整个句子级别的状态。它使用全局句子级别的表示形式进行分类任务。这些方法将文档或句子视为单词节点的图，或依靠文档引用关系来构造图。[107]将文档和单词作为节点来构造语料图（因此是异构图），并使用Text GCN来学习单词和文档的嵌入。情感分类也可以看作是文本分类问题，[60]提出了Tree-LSTM方法。

序列标签：由于GNN中的每个节点都有其隐藏状态，因此如果我们将句子中的每个单词都视为一个节点，则可以利用隐藏状态来解决序列标记问题。[62]利用句子LSTM标记序列。它已经对POS标记和NER任务进行了实验，并取得了可喜的性能。

语义角色标记是序列标记的另一项任务。[108]提出了句法GCN来解决这个问题。在带有标记边的直接图形上运行的语法GCN是GCN的特殊变体[2]。它集成了沿边的门，使模型可以调节各个依赖边的贡献。句法依赖树上的句法GCN用作句子编码器，以学习句子中单词的潜在特征表示。[108]也揭示了GCN和LSTM在任务上是功能互补的。

神经机器翻译：神经机器翻译任务通常被认为是序列到序列的任务。[66]介绍了注意力机制，并替换了最常用的循环层或卷积层。实际上，Transformer假设语言实体之间具有完全连接的图结构。

GNN的一种流行应用是将语法或语义信息合并到NMT任务中。[109]在语法可识别的NMT任务上使用了语法GCN。[110]使用句法GCN合并有关源语句谓词结构的信息（即语义角色表示），并比较仅将句法或语义信息或将这两种信息合并到任务中的结果。[38]在语法感知的NMT中使用GGNN。通过将边变成额外的节点，它将语法相关性图转换为称为Levi图的新结构，因此可以将边缘标签表示为嵌入。

关系提取：提取文本中实体之间的语义关系是一项重要且经过充分研究的任务。一些系统将此任务视为两个独立任务的管道，分别称为实体识别和关系提取。[111]提出了一种使用双向顺序和树状结构的LSTM-RNN的端到端关系提取模型。[113]提出了图卷积网络的扩展，它是为关系提取量身定制的，并将修剪策略应用于输入树。

跨句N元关系提取可检测多个句子中n个实体之间的关系。[44]探索了基于图LSTM的跨语句n元关系提取的通用框架。它将输入图分为两个DAG，而重要的信息可能会在拆分过程中丢失。[112]提出了一种图态LSTM模型。它保留了原始的图形结构，并通过允许更多的并行化来加快计算速度。

事件提取：事件提取是识别文本中指定类型事件的实例的重要信息提取任务。[114]研究了基于依赖树的卷积神经网络（确切地说是语法GCN）来执行事件检测。[115]提出了一个联合多个事件提取（JMEE）框架，通过引入句法捷径弧来增强信息流到基于注意力的图卷积网络以建模图信息，从而联合提取多个事件触发器和参数。

其他应用：GNN也可以应用于许多其他应用程序。关于AMR到文本生成任务的工作有几篇。在这一领域已经提出了基于Sentence-LSTM的方法[116]和基于GGNN的方法[38]。[60]使用Tree LSTM建模两个句子的语义相关性。[117]利用句子LSTM解决了多跳阅读理解问题。另一个重要方向是关系推理，提出了关系网络[96]，交互网络[4]和递归关系网络[118]来解决基于文本的关系推理任务。以上引用的作品并非详尽无遗，我们鼓励读者找到他们感兴趣的图神经网络的更多作品和应用领域。

3.3其他场景

除了结构和非结构方案外，图神经网络还扮演着其他重要角色。在本小节中，我们将介绍生成图模型和GNN的组合优化。

3.3.1生成模型

现实世界图形的生成模型已为其重要应用引起了广泛关注，这些重要应用包括对社交互动进行建模，发现新的化学结构以及构建知识图。由于深度学习方法具有强大的能力来学习图的隐式分布，因此近来神经图生成模型激增

NetGAN [140]是建立神经图生成模型的第一批工作之一，该模型通过随机游走生成图。它把图生成的问题转化为步行生成的问题，该问题以来自特定图的随机游走作为输入，并使用GAN架构训练步行生成模型。虽然生成的图保留了原始图的重要拓扑特性，但是节点数在生成过程中无法更改，这与原始图相同。GraphRNN [148]设法通过逐步生成每个节点的邻接向量来生成图的邻接矩阵，从而可以输出具有不同数量节点的所需网络。

MolGAN [143]没有立即生成邻接矩阵，而是立即预测了离散图结构（邻接矩阵），并利用不变排列的鉴别器来解决邻接矩阵中的节点变量问题。此外，它还针对基于RL的化学性质对期望的化学性质应用了奖励网络。此外，[141]提出了受约束的变分自动编码器，以确保生成的图的语义有效性。并且，GCPN [142]通过强化学习并入了特定领域的规则。

[149]提出了一个模型，该模型顺序地生成边和节点，并利用图神经网络提取当前图的隐藏状态，该状态用于确定顺序生成过程中下一步的动作。

3.3.2组合优化

图上的组合优化问题是一类NP难题，引起了各个领域科学家的广泛关注。一些特定的问题，例如旅行商问题（TSP）和最小生成树（MST），已经获得了各种启发式解决方案。近年来，使用深度神经网络解决此类问题已成为热点，并且一些解决方案由于其图结构而进一步利用了图神经网络。

[150]首先提出了一种深度学习的方法来解决TSP。他们的方法由两部分组成：用于参数化奖励的指针网络[151]和用于培训的策略梯度[152]模块。这项工作已被证明与传统方法具有可比性。但是，指针网络专为诸如文本之类的顺序数据而设计，而定序编码器更适合此类工作。

[153]和[139]通过包括图神经网络改进了上述方法。先前的工作首先从structure2vec [94]获取节点嵌入，然后将其嵌入Q学习模块中以进行决策。后者构建了一个基于注意力的编码器-解码器系统。通过用基于注意力的解码器替换强化学习模块，培训效率更高。这些工作比以前的算法具有更好的性能，证明了图神经网络的表示能力。

[137]专注于二次分配问题，即 测量两个图的相似度。基于GNN的模型独立学习每个图的节点嵌入，并使用注意力机制将其匹配。
即使在标准的基于松弛的技术似乎遭受损失的情况下，该方法也提供了令人感兴趣的良好性能。

4.开放的问题

尽管GNN在不同领域取得了巨大的成功，但值得注意的是，GNN模型不足以在任何条件下为任何图形提供令人满意的解决方案。在本节中，我们将陈述一些尚待进一步研究的问题。

浅结构（层数问题）：传统的深度神经网络可以堆叠数百层以获得更好的性能，因为更深的结构具有更多的参数，从而显着提高了表达能力。但是，图神经网络总是很浅，大多数不超过三层。如[82]中的实验所示，堆叠多个GCN层将导致过度平滑，也就是说，所有顶点都将收敛到相同的值。尽管一些研究人员设法解决了这个问题[59]，[82]，但它仍然是GNN的最大局限。设计真正的深度GNN是未来研究的一个令人兴奋的挑战，并且将对理解GNN做出巨大贡献。

动态图（变化的结构）：另一个具有挑战性的问题是如何处理具有动态结构的图。静态图是稳定的，因此可以对其进行建模，而动态图则引入了变化的结构。当边缘和节点出现或消失时，GNN无法自适应地更改。动态GNN正在积极研究中，我们相信这将成为通用GNN稳定性和适应性的重要里程碑。

非结构性场景：尽管我们已经讨论了GNN在非结构性场景中的应用，但是我们发现没有最佳方法可以从原始数据生成图形。在图像领域，一些工作利用CNN获得特征图，然后对其进行升采样以形成超像素作为节点[63]，而其他工作则直接利用某些对象检测算法来获取对象节点。在文本域[129]中，有些作品采用句法树作为句法图，而另一些则采用完全连接的图。因此，找到最佳的图形生成方法将为GNN可以做出贡献的领域提供更大的范围。

可扩展性：对于几乎所有的图形嵌入算法而言，如何在网络规模条件（如社交网络或推荐系统）中应用嵌入方法一直是致命的问题，GNN也不例外。扩展GNN十分困难，因为许多核心步骤在大数据环境中消耗大量计算资源。关于此现象有几个示例：首先，图数据不是规则的欧几里得，每个节点都有自己的邻域结构，因此无法应用批处理。这样，当有数百万个节点和边时，计算图拉普拉斯算子也是不可行的。此外，我们需要指出，缩放比例决定了算法是否能够被实际应用。一些工作已经提出了解决这个问题的方法[77]，我们正在密切注意进展。

5.结论

在过去的几年中，图神经网络已成为强大的实用工具，可用于图领域的机器学习任务。这一进步归因于表达能力，模型灵活性和训练算法的进步。在这项调查中，我们对图神经网络进行了全面的回顾。对于GNN模型，我们介绍其按图类型，传播类型和训练类型分类的变体。此外，我们还总结了几个通用框架以统一表示不同的变体。在应用程序分类方面，我们将GNN应用程序分为结构性场景，非结构性场景和其他场景，然后对每种场景中的应用程序进行详细的回顾。最后，我们提出了四个开放性问题，这些问题指示图神经网络的主要挑战和未来研究方向，包括模型深度，可伸缩性，处理动态图的能力和非结构化场景。