数据结构——排序(详细,通俗易懂)
目录
排序的概念
排序的分类
插入排序
选择排序
交换排序
归并排序
-
排序的概念
排序就是一系列数据,按照某个关键字(例如:销量,价格),进行递增或者递减的顺序排列起来.
-
排序的分类
-
插入排序
- ——直接插入排序
把待排序的数据插入到已经排好序的数据中,直到所有的数据插入完成,即就是直接插入排序。(如流行于陕西一带的纸牌游戏,挖坑)一般待排序的区间是第二个数到最后一个数。例如下面的例子就是待排序区间从 7 到 8。把第一个数当作已经排序的数据
//C语言
void Insert_Sort(int arr[], int size)
{
assert(arr);
int i;//待插入元素的下标
int j; //需要进行比较的元素的下标。在i前面的元素都是已经排序好的元素。
int temp; //进行存储。在插入的过程中,需要进行移动。
for (i = 1; i < size; ++i)//1、从第二个元素插入,保证有可以比较的元素。
{
temp = arr[i]; //需要插入的元素,进行保存。
for (j = i - 1; j >= 0; --j)//在已经有序的数列中,进行比较。
{
if (temp < arr[j]) //进行升序排序。如果待插入的元素小于它前一个元素arr[j],
//就把带插入元素向前移动,那么 j 位置的元素
//就需要向后移动一个位置,直接覆盖就好,因为已经保存了
{
arr[j + 1] = arr[j];
}
else //如果带插入元素不大于前一个元素,就停止
{
break;
}
}
arr[j + 1] = temp;//即为被插入元素的位置
}
}- ——希尔排序
希尔排序实在前面直接插入排序的基础上进行改进的一种排序。直接插入排序的变量 i 其实就是一个间隔,而希尔排序的间隔不是 1,它的间隔逐渐缩小直到为 1 的一种排序,因此又叫缩小增量法。它是对直接插入排序算法的优化,当间隔不为 1 的时候,都是预排序。第一次的间隔是 数据长度的三分之一再加一。即 gap = size / 3 + 1
//C语言
void InsertSortWithgap(int arr[], int size, int gap)
{
assert(arr);
int i;
int j;
int temp;
for (i = gap; i < size; ++i)//从下标为gap的元素作为带插入元素
{
temp = arr[i];//存储gap下标的元素
for (j = i - gap; j >= 0; j -= gap)//从第 0 个元素进行比较
{
if (temp > arr[j])//降序
{
arr[j + gap] = arr[j];//gap位置的元素换成 j 所在下标的元素
}
else
{
break;
}
}
arr[j + gap] = temp;//j 所在下标位置存储 temp
}
}
//希尔
void ShellSort(int arr[], int size)
{
int gap = size;
while (1)
{
gap = gap / 3 + 1;//改变gap 的值
InsertSortWithgap(arr, size, gap);
if (gap == 1)
{
break; //gap的值为一时停止
}
}
}-
选择排序
- 直接选择排序
选择排序就是在待排序的数据中选择一个最大的或者最小的放在带待排序数据的末尾。也可以是已经排好序的数据的开头。
//C语言
//选择排序
void Choice_Sort2(int arr[], int size)
{
for (int i = 1; i < size; ++i)//从下标为1 开始,找size - 1次
{
int max = 0;//假设最大的数的下标是第 0 个
for (int j = 1; j <= size - i; ++j)//从下标为 1 的元素开始比较。直到最后一个数
{
if (arr[j] > arr[max])
{
max = j;//如果找到比下标为max的元素还大的元素则把max的值进行改变
}
}
int temp = arr[size - i];
arr[size - i] = arr[max];
arr[max] = temp;
}
}- 堆排序
堆排序就要用到前面学到的数据结构二叉树的知识了。堆的作用是什么呢?就是寻找最值。所以根节点肯定最大(大堆)或者最小(小堆)。我们把根节点和最后一个结点进行交换,数组最后一个数肯定就是最大或者最小的。最后又在剩下的数据里面建堆。 要注意的是升序建大堆,降序建小堆,下面复习一下堆的知识。
//C语言
//向下调整
void Adjust_down(int arr[], int size, int root)
{
while (1)
{
int left = root * 2 + 1;
int right = root * 2 + 2;
int min = left;//最小的为最左孩子
if (left >= size)//没有孩子结点
{
return;
}
if (right < size && arr[right] < arr[left])//有右孩子
{
min = right;
}
if (arr[root] <= arr[min])//根节点已经是最小
{
return;
}
int temp = arr[root];
arr[root] = arr[min];
arr[min] = temp;
root = min;
}
}
//建堆
void CreateBigHeap(int arr[], int size)
{
//对左子树建堆,再对右子树建堆
int notlevel = (size - 2) / 2;//从最后一个非叶子结点开始调整
while (notlevel >= 0)
{
Adjust_down(arr, size, notlevel);
--notlevel;
}
}
void HeapSort(int arr[], int size)
{
//建堆
CreateBigHeap(arr, size);
for (int temp = 1; temp < size; ++temp)
{
int t = arr[0];
arr[0] = arr[size - temp]; //这个值就是最后一个叶子结点。
arr[size - temp] = t;
Adjust_down(arr, size-temp,0);//从根节点开始调整
}
}-
交换排序
- 冒泡排序
冒泡排序是我们最熟悉的一种排序了吧,它的过程就是从第一个数开始,和第二个数比较,满足条件就进行交换,然后第二个数和第三个数进行比较满足进行交换,直到最后一个数,这是一个“泡”已经冒出。现在有从开始比较,这个时候总的比较的数减少一个,因为“泡”已经冒出了。冒泡排序一共会进行 size - 1次冒泡,每次的比较次数为size - i,i是比较的第几次。
//C语言
void Bubble_Sort(int arr[], int size)
{
assert(arr);
for(int row = 0; row < size - 1; ++row)
{
int flag = 1;
for(int col = 0; col < size - row - 1; ++col)//col是从0开始的
{
if (arr[col] < arr[col + 1])
{
int temp = arr[col + 1];
arr[col + 1] = arr[col];
arr[col] = temp;
flag = 0;
}
}
if (flag == 1)
{
break;
}
}
}- 快速排序
快速排序一共分为三大步。
1、选择一个基准值:基准值就是参考的一个数。这个基准值我们一般选取最左边或者最右边,有助于下边的步骤进行。
2、遍历整个区间,把除基准值之外的所有数据与基准值进行比较,并进行数据移动,满足
1>比基准值小的数放在基准值的左边
2>比基准值大的数放在基准值的右边
(一开始的基准值不是在最左边或者最右边吗,怎么把数据放在它的左右呢?这个然会有函数处理)
3、分治算法:利用递归,让基准值的左右边的区间也重复上面的操作,直到区间的size为 0 或者 1。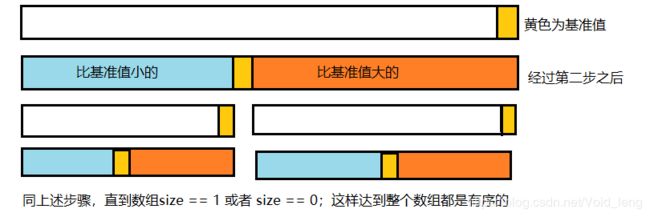
下面来就来处理怎么把数放在基准值的左右,也就是重要的第二步。一共三种方法。
✦hover法
//C语言
int partition_1(int arr[], int left, int right)
{
int begin = left; //left == 数组的第一个元素的下标。并不一定是 0.比如在基准值右边的区间
int end = right;//right == 数组的最后一个元素的下标
while (begin < end) //当两个元素不相遇的时候。
{
while (begin < end && arr[begin] <= arr[right])
{
++begin;//满足条件比较下一个元素,向右移动
}
while (begin < end && arr[end] >= arr[right])
{
--end;//向左移动
}
int temp = arr[begin]; //当begin和end没有相遇,且不满足条件时。交换两个元素
arr[begin] = arr[end];
arr[end] = temp;
}
int temp = arr[begin];
arr[begin] = arr[right];
arr[right] = temp;//最后把基准值填在中间
return begin;//返回基准值的下标
} ✦挖坑法
挖坑法和hover法差不多的。
//C语言
int partition_2(int arr[], int left, int right)//挖坑法
{
int begin = left;
int end = right;
int pivot = arr[right];//保存了基准值
while (begin < end)
{
while (begin < end && arr[begin] <= pivot)
{
++begin;
}
arr[end] = arr[begin];//此时把begin当成坑,把begin的数据放入end
while (begin < end && arr[end] >= pivot)
{
--end;
}
arr[begin] = arr[end];//把end当成坑。
}
arr[begin] = pivot;//把基准值 放入最后的坑
return begin;
}- 1>为什么要从基准值的相反的地方开始?
为了防止一比到底,导致最后一个数没有比较。
例如:1 3 4 2 假设1是基准值,从2开始,即就是end
这个时候一直是--end,直到遇见begin。但是begin上的元素是1,但退出循环后,会和基准值进行交换,但是arr[begin]没有和基准值进行比较。造成 小于基准值的数也放到了右边
- 2>arr[begin] <= arr[right] 为是那么要取等?
为了防止死循环。
例如:1 1 1 1 假设右边的1是基准值。如果没有等号,begin不走,end也不走,这个时候就是死循环。
✦前后下标法
//C语言
int partition_3(int arr[], int left, int right)
{
int div = left;
for (int cur = left ; cur < right; ++cur)
{
if (arr[cur] < arr[right])// 如果遇到小于基准值的数就与div的位置上的数交换
{
int temp = arr[cur];
arr[cur] = arr[div];
arr[div] = temp;
++div;
}
}
int temp = arr[right];//退出循环后,放置基准值
arr[right] = arr[div];
arr[div] = temp;
return div;
}下面来进行最后一步。分治。
//C语言
void QuickSort(int arr[], int left, int right)
{
if (left >= right)
{
return;
}
int povit = partition_3(arr, left, right);//用的前后下标法
QuickSort(arr, left, povit - 1);//递归调用
QuickSort(arr, povit + 1, right);
}
void Quick_Sort(int arr[], int size)
{
QuickSort(arr, 0 , size -1);
}上面的快速排序,是个通俗易懂的版本,比较繁琐,把步骤分开了说。当然有精简版,但重要的应该是理解。上述递归也可以用循环加栈的方式。
-
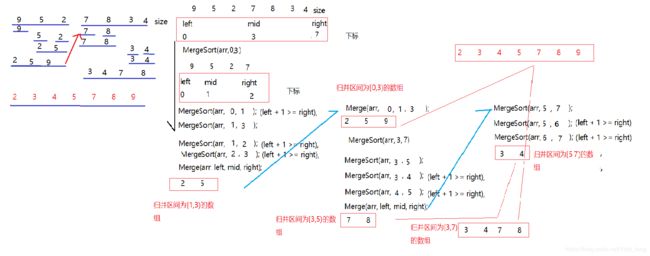
归并排序
归并排序也需要借助分治算法。但是这个的基准值是一直是数组的中间那个数,而不是像快速排序一样选边上的数据作为基准值。
//C语言
void MergeSort(int arr[], int left, int right)
{
if (left + 1 >= right)//直到找到一个数,便是一定有序的
{
return;
}
int mid = left + (right - left) / 2;//找到中间值
MergeSort(arr, left, mid);//递归,后面有流程图,知道递归就看的懂了
MergeSort(arr, mid, right);
//归并
//就是两个有序数组进行合并
Merge(arr, left, mid, right);//后面实现
}
void Merge_Sort(int arr[], int size)
{
MergeSort(arr, 0 , size);
}因为编辑器的原因,图只能这个样子了。
//C语言
//两个有序数组的归并
void Merge(int arr[], int left, int mid, int right)
{
int size = right - left;
int *extra = (int*)malloc(sizeof(int)*size);
int left_p = left;
int right_p = mid;
int extra_p = 0;
while (left_p < mid && right_p < right)
{
if (arr[left_p] <= arr[right_p])
{
extra[extra_p] = arr[left_p];
++left_p;
}
else
{
extra[extra_p] = arr[right_p];
++right_p;
}
++extra_p;
}
while (left_p < mid)
{
extra[extra_p] = arr[left_p];
++left_p;
++extra_p;
}
while (right_p < right)
{
extra[extra_p] = arr[right_p];
++right_p;
++extra_p;
}
for (int i = 0; i < size; ++i)
{
arr[left + i] = extra[i];
}
free(extra);
}