Huffman树及Huffman编码,译码的算法实现
参考:https://blog.csdn.net/curson_/article/details/53771386
本来以为这个实验一会儿就可以搓出来,最后跟着要求搓了几个小时,菜是原罪,菜是真的菜,(助教小姐姐很好)
要求:
1、输入一段100—200字的英文短文,存入一文件a中。
2、写函数统计短文出现的字母个数n及每个字母的出现次数
3、写函数以字母出现次数作权值,建Haffman树(n个叶子),给出每个字母的Haffman编码。
4、用每个字母编码对原短文进行编码,码文存入文件b中。
5、用Haffman树对b中码文进行译码,结果存入文件c中,比较a,c是否一致,以检验编码、译码的正确性。
介绍:
哈夫曼树(Huffman Tree),又叫最优二叉树,指的是对于一组具有确定权值的叶子结点的具有最小带权路径长度的二叉树。
在通信及数据传输中多采用二进制编码。为了使电文尽可能的缩短,可以对电文中每个字符出现的次数进行统计。设法让出现次数多的字符的二进制码短些,而让那些很少出现的字符的二 进制码长一些。
算法思想:
参考:https://blog.csdn.net/wtfmonking/article/details/17150499#
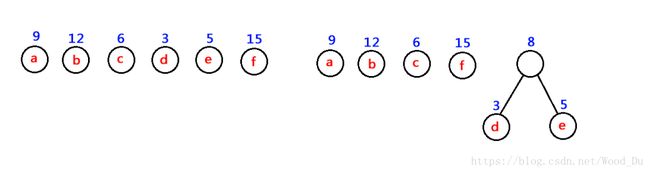
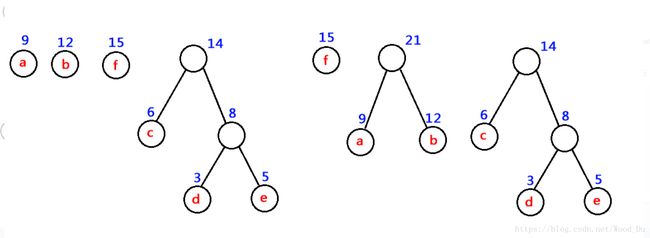
(1) 以权值分别为W1,W2...Wn的n各结点,构成n棵二叉树T1,T2,...Tn并组成森林,F={T1,T2,...Tn},其中每棵二叉树 Ti仅有一个权值为 Wi的根结点;
(2) 在F中选取两棵根结点权值最小的树作为左右子树构造一棵新二叉树,并且置新二叉树根结点权值为左右子树上根结点的权值之和(根结点的权值=左右孩子权值之和,叶结点的权值= Wi)
(3) 从F中删除这两棵二叉树,同时将新二叉树加入到F中;
(4) 重复(2)、(3)直到F中只含一棵二叉树为止,这棵二叉树就是Huffman树。
如下图:

具体算法:
1、 存储结构:
数组长度为带权值的元素个数n额的俩倍,其中0号单元空置,1到n号单元存放只有当个节点的树(没有父节点,parent为0),
n+1之后的元素存放分别以前n个节点中的最小权重节点及次小权重节点为做左孩子和右孩子的双亲:
using namespace std;
int a[27]; //存储每个字母出现的次数
char s[1000000];
//int n;
int m; //一共多少个点
int num=0; //叶子节点个数
int len;
map<char,int> v; //对应的字母和出现的次数
typedef struct{
char c;
int weight; //权重
int parent,lchild,rchild; //节点的双亲下标,左右孩子的下标
char code; //结点编号
}htnode,*huffmantree;2、 统计短文出现的字母种数和每个字母出现的次数
读入a.txt文件中的内容,a[0]-a[25]表示字母a-z出现的次数,s[]为读入的英文短文。结果若a[i]>0,则表示对应的字母出现,可统计出现的字母种数和字母出现的次数。
并将字母和对应的出现次数放入map
//统计短文出现的字母种数和每个字母出现的次数
void f1(){
FILE *fi=freopen("a.txt","r",stdin);
gets(s); //gets()读入时空格也读入,直到遇到回格键
len=strlen(s);
cout<//短文长度
for(int i=0;iif(s[i]-'a'>=0&&s[i]-'a'<=25){
a[s[i]-'a']++;
}
if(s[i]-'A'>=0&&s[i]-'A'<=25){
a[s[i]-'A']++;
}
}
// int num=0;
for(int i=0;i<26;i++){
if(a[i]>0){
num++;
char cha;
cha='a'+i;
cout<": "<" "; //每个字母出现的次数 作为权
v.insert(pair<char,int>(cha,a[i]));
}
}
cout<printf("字母出现的种数:");
cout<cout< 3、 创建huffmantree
创建huffmantree,num为叶子节点个数,m为num个叶子节点对应的huffmantree的总节点数。所以m=2*num-1。初始化编码,只要不是0或1即可。初始化每个节点的值为0。然后将容器中的字母和对应的次数放入ht[1].c和ht[1].weight-ht[num].c和ht[num].weight中,从num+1开始添加节点,开始找前面节点中最小的两个值,找到节点必须满足双亲结点为0,且左边小于等于右边,将两节点的双亲设置为新节点的位置,此时两节点的双亲结点不为0,两节点在下个循环中也就不会参与比较。并将左孩子的编码设为’0’,右孩子的编码设为’1’。同时添加新节点,ht[i].lchild,ht[i].rchild,新节点的权值为孩子节点权值之和。
//创建huffmantree
void creathuffmantree(huffmantree &ht,int num,map<char,int> v){
m=2*num-1; //num个叶子的huffman树共有2num-1个节点
ht = new htnode[m+1]; //htnode[0]不存节点
for(int i=1;i<=m;i++){ //初始化每个节点的值
ht[i].parent=ht[i].lchild=ht[i].rchild=0;
ht[i].code='9'; //初始化编码
}
map<char, int>::reverse_iterator iter;
int j=1;
for(iter = v.rbegin(); iter !=v.rend(); iter++){
cout<first<<" "<second<first;
ht[j].weight=iter->second;
j++;
}
//test
for(int i=1;i<=num;i++){
cout<": "<0].weight=num;
for(int i=num+1;i<=m;i++){//已有num个节点,从num+1开始添加节点 共添加num-1个,也就是到m
int s1,s2;
Selectmin(ht,i,s1,s2); //传入添加节点的位置 返回两个最小值s1<=s2
//将两节点的双亲设置为新节点的位置
ht[s1].parent=i;
ht[s2].parent=i;
ht[s1].code='0'; //编码
ht[s2].code='1';
//添加新节点,左右孩子
ht[i].lchild=s1;
ht[i].rchild=s2;
ht[i].weight=ht[s1].weight+ht[s2].weight;//新节点权值
}
} void Selectmin(huffmantree ht,int num2,int &s1,int &s2)函数:
此函数用于选择两个最小的值,且s1<=s2,添加新的节点,构造huffman树;
//选择两个权值最小的点
void Selectmin(huffmantree ht,int num2,int &s1,int &s2){
s1=s2=0; //初始化两个最小节点的位置
int i;
for(i=1;i<=num2;i++){
if(ht[i].parent==0){
if(s1==0) s1=i;
else{
s2=i;
break;
}
}
}
if(ht[s1].weight>ht[s2].weight){
int t=s1;
s1=s2;
s2=t;
}
for(i=i+1;iif(ht[i].parent==0){
if(ht[i].weightelse if(ht[i].weight 创建的huffman数的相关信息输出:
WPL:树的所有叶结点的带权路径长度之和,称为树的带权路径长度表示为WPL。
WPL=(W1*L1+W2*L2+W3*L3+…+Wn*Ln)。
N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明哈夫曼树的WPL是最小的。
WPL是衡量一个带权二叉树优劣的关键。 无论如何,对于n个带权节点,总可以用他们作为叶节点构造出一颗最小WPL值得树,并称满足这个条件的二叉树为哈夫曼树。
输出叶子创建的huffmantree各叶子节点的的信息。
//计算huffman树总路径长度
int huffmantreeWPL(huffmantree ht,int i,int d){ //传入huffman树,节点位置,节点深度
if(ht[i].lchild==0&&ht[i].rchild==0){ //叶子节点;算出该节点路径
return ht[i].weight*d;
}
else{ // 若该节点不是叶子节点,则该节点的路径等于左右孩子的路径和
return huffmantreeWPL(ht,ht[i].lchild,d+1)+huffmantreeWPL(ht,ht[i].rchild,d+1);
}
}
//输出huffman树各节点的信息
void printf(huffmantree ht){
cout<<"你能看懂这个关系吗"<//改进
/***
叶子节点: f 节点的序号: 1 权值: 5 父亲节点序号: 7 左孩子节点序号: 0 右孩子节点序号: 0
叶子节点: d 节点的序号: 2 权值: 3 父亲节点序号: 6 左孩子节点序号: 0 右孩子节点序号: 0
叶子节点: c 节点的序号: 3 权值: 2 父亲节点序号: 5 左孩子节点序号: 0 右孩子节点序号: 0
叶子节点: a 节点的序号: 4 权值: 1 父亲节点序号: 5 左孩子节点序号: 0 右孩子节点序号: 0
叶子节点: 节点的序号: 5 权值: 3 父亲节点序号: 6 左孩子节点序号: 4 右孩子节点序号: 3
叶子节点: 节点的序号: 6 权值: 6 父亲节点序号: 7 左孩子节点序号: 2 右孩子节点序号: 5
叶子节点: 节点的序号: 7 权值: 11 父亲节点序号: 0 左孩子节点序号: 1 右孩子节点序号: 6
***/
for(int i=1;i<=m;i++){
cout<<"叶子节点: "<" ";
// cout<<"第 "<
cout<<"节点的序号: "<" " ;
cout<<"权值: "<" ";
cout<<"父亲节点序号: "<" ";
cout<<"左孩子节点序号: "<" ";
cout<<"右孩子节点序号: "<" "< 4、编码:
输出叶子节点的编码:
//输出各叶子节点的编码
void Encoding(huffmantree ht,int i){
if(ht[i].parent==0){
return;
}
else{
Encoding(ht,ht[i].parent);
}
cout<//输出叶子节点的编码
void huffmantreeEncoding(huffmantree ht){
// freopen("b.txt","w",stdout);
for(int i=1;i<=num;i++){ //只输出前num,即叶子节点的编码
if(ht[i].lchild==0&&ht[i].rchild==0) //如果该节点为叶子节点
{
// char ch;
cout<" 权值:";
printf("%d:",ht[i].weight);
cout<<"编码:";
Encoding(ht,i); //用递归输出该节点的编码
printf("\n");
}
}
} 对原文进行编码,存入b.txt中:
void trans(huffmantree ht){
FILE *fi=freopen("a.txt","r",stdin);
FILE *fo=freopen("b.txt","w",stdout);
gets(s); //gets()读入时空格也读入,直到遇到回格键
len=strlen(s);
for(int i=0;ifor(int j=1;j<=num;j++){
if(s[i]==ht[j].c){
Encoding(ht,j);
}
}
if(s[i]<'a'||s[i]>'z'){
cout<// cout<
} 5.译码:用Haffman树对b中码文进行译码,结果存入文件c中,比较a,c是否一致,以检验编码、译码的正确性。
//用Haffman树对b中码文进行译码,结果存入文件c中,
//比较a,c是否一致,以检验编码、译码的正确性。
void yima(huffmantree ht){
FILE *fi1=freopen("a.txt","r",stdin);
gets(s);
//int len1=strlen(s);
fclose(fi1);
FILE *fi2=freopen("b.txt","r",stdin);
char b[1010];
gets(b);
//int len2=strlen(b);
fclose(fi2);
freopen("c.txt","w",stdout);
int i=m;
int j=0;
while(b[j]!='\0'){ //遍历字符数组/编码串
if(b[j]=='0')
i=ht[i].lchild; //走向左孩子
else if(b[j]=='1')
i=ht[i].rchild; //走向右孩子
//if(b[j]<'a'||b[j]>'z'){
else{
printf("%c",b[j]); //为什么不能用cout
//cout<
}
if(ht[i].lchild==0){ //看是否该节点为叶子节点
printf("%c",ht[i].c);//是的话输出,并返回根节点
i=m;
}
j++; //无论是否找到叶子节点都读取下一个编码串字符
}
} main函数:
int main()
{
huffmantree ht;
f1();
cout<cout<cout<<"WPL = "<0)<printf(ht);
huffmantreeEncoding(ht);
trans(ht);
yima(ht);
return 0;
} 源码:
https://download.csdn.net/download/wood_du/10423300
https://github.com/Du-Sen-Lin/acacac