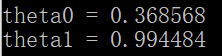C++实现梯度下降(gradient descent)算法

0.综述

算法很好理解，求偏导然后更新theta矩阵，可以解决线性回归相关的问题。

1.几点说明

a.代码中的Matrix类是我自己写的一个矩阵相关的类，支持矩阵的加减乘除，转置运算。

b.关于学习速率alpha的确定，我的建议是alpha要保证每次梯度下降theta矩阵内元素的变化在0.01-0.05内。

c.数据超过500时，即max1，max2超过500时，使用默认的栈可能会导致栈内存不够，解决方法点这里。

2.一个直观的样例

样例点这里

数据集为（1，1）（2，2）（3，3）。。。。。

取alpha = 0.003

拟合的结果显然应该为theta0 = 0, theta1 = 1。

我们运行程序的结果是       基本符合要求。

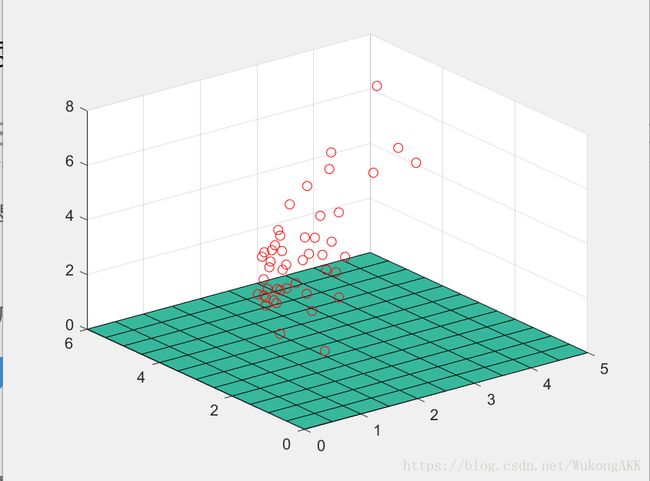
3.三维空间的一个样例

样例点这里

利用matlab展示数据

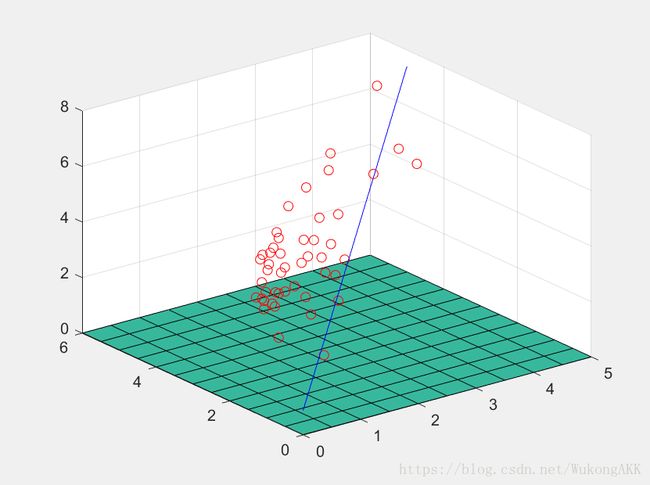
运行程序得到theta矩阵，iteration = 50000, alpha = 0.05, 画出拟合后的直线 

4.源代码 

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int max1 = 1005;
const int max2 = 1005;
int data_num, fea_num;

class Matrix{
	public:
		Matrix(int x = 0) : ro(x) {}
		Matrix(int x, int y,  double a[max1])
		: ro(x), co(y){
			for(int i = 1; i <= ro; i++)	el[i][1] = a[i];
		}
		Matrix(int x, int y, double a[max1][max2])
		: ro(x), co(y){
			for(int i = 1; i <= ro; i++)
			for(int j = 1; j <= co; j++)
				el[i][j] = a[i][j];
		}
		
		
		Matrix sum1();
		Matrix transpose();
		int row() const { return ro; }
		int col() const { return co; }
		double ele(const int& i, const int& j) const { return el[i][j]; }
		void change(int i, int j, double x) { el[i][j] = x; }
		double sum() { double s = 0; for(int i=1;i<=ro;i++)for(int j=1;j<=co;j++)s+=el[i][j];return s; }
		void print() { for(int i=1;i<=ro;i++){for(int j=1;j<=co;j++)printf("%.3lf ",el[i][j]);printf("\n"); } }
	
	
	private:
		int ro;
		int co;
		double  el[max1][max2];
};
Matrix X, Y;

Matrix Matrix::sum1(){
	double temp[max1];
	memset(temp, 0, sizeof(temp));
	for(int i = 1; i <= this->ro; i++)
	for(int j = 1; j <= this->co; j++)
		temp[i] += el[i][j];
	return Matrix(this->ro, 1, temp);
}

Matrix Matrix::transpose(){
	double temp[max1][max2];
	int row = this->row();
	int col = this->col();
	for(int i = 1; i <= row; i++)
	for(int j = 1; j <= col; j++)
		temp[j][i] = this->ele(i, j);
	return Matrix(this->col(), this->row(), temp);
}

inline	
Matrix operator + (const Matrix& lhs, const Matrix& rhs){
	double temp[max1][max2];
	if(lhs.row() != rhs.row() || lhs.col() != rhs.col())
		return Matrix(-1);
	for(int i = 1; i <= lhs.row(); i++)
	for(int j = 1; j <= lhs.col(); j++)
		temp[i][j] = lhs.ele(i, j) + rhs.ele(i, j);
	return Matrix(lhs.row(), lhs.col(), temp);
}

inline
Matrix operator - (const Matrix& lhs, const Matrix& rhs){
	double temp[max1][max2];
	for(int i = 1; i <= rhs.row(); i++)
	for(int j = 1; j <= rhs.col(); j++)
		temp[i][j] = -rhs.ele(i, j);
	return  lhs + Matrix(rhs.row(), rhs.col(), temp);
}

inline
Matrix operator * (const Matrix& lhs, const Matrix& rhs){
	if(lhs.col() != rhs.row())
		return Matrix(-1);
	double temp[max1][max2];
	memset(temp, 0, sizeof(temp));
	for(int i = 1; i <= lhs.row(); i++)
	for(int j = 1; j <= rhs.col(); j++) 
	for(int k = 1; k <= lhs.col(); k++)
		temp[i][j] += lhs.ele(i, k) * rhs.ele(k, j);
	return Matrix(lhs.row(), rhs.col(), temp);
}

inline
Matrix operator / (const Matrix& lhs, const int& rhs){
	double temp[max1][max2];
	for(int i = 1; i <= lhs.row(); i++)
	for(int j = 1; j <= lhs.col(); j++)
		temp[i][j] = lhs.ele(i, j) / rhs;
	return Matrix(lhs.row(), lhs.col(), temp);
}

void read(){
	scanf("%d%d", &data_num, &fea_num);
	double temp[max1][max2];
	double temp2[max1];
	for(int i = 1; i <= data_num; i++)
		temp[i][1] = 1;
	for(int i = 1; i <= data_num; i++){
		for(int j = 1; j <= fea_num; j++)
			scanf("%lf", &temp[i][j+1]);
		scanf("%lf", &temp2[i]);
	}
	X = Matrix(data_num, fea_num+1, temp);
	Y = Matrix(data_num, 1, temp2);
}

void gradient_descent(Matrix& theta, int iteration, double alpha)
{
	//X.print();
	//theta.print();
	//(X*theta - Y).print();
	//(X*theta - Y).transpose().print();
	//((X*theta - Y).transpose() * (X*theta - Y)).print();
	//Matrix H = X*theta;
	//Matrix Z = H - Y;
	//Z.print();
	for(int i = 1; i <= iteration; i++){
		double cost = ((X*theta - Y).transpose() * (X*theta - Y)).sum() / (2*data_num);
		printf("iteration %d\t  cost = %lf\n", i, cost);
		//X.transpose().print();
		//(X.transpose() * ((X*theta) - Y)).print();
		theta = theta - (X.transpose() * ((X*theta) - Y)).sum1() / (data_num/alpha);
		//theta.print();
	}
}


Matrix solve(){
	double temp[max1];
	for(int i = 1; i <= X.col(); i++)
		temp[i] = rand()%1000/100;
	Matrix theta(X.col(), 1, temp);
	gradient_descent(theta, 50000, 0.005);
	return theta;
}

void print(const Matrix& ans){
	for(int i = 1; i <= ans.row(); i++)
		printf("theta%d = %lf\n", i-1, ans.ele(i, 1));
    //X.print();
	//theta.print();
	//(X*ans - Y).print();
	//(X*theta - Y).transpose().print();
	//((X*ans - Y).transpose() * (X*ans - Y)).print();
	//Matrix H = X*theta;
	//Matrix Z = H - Y;
	//Z.print();
}
		
int main()
{
	freopen("ztest.txt","r",stdin);
	srand(time(NULL));
	read();
	print(solve());
	return 0;
}