关于bp神经网络的原理与自建研究以及计算结果。

预备工作

说起预备工作，一般总得介绍一下神经网络的结构啥的，这些东西呢我就不多做介绍，从一开始接触这东西，乍一看，一元的神经网络，不就是一个经典的线性规划模型么，（至于线性规划，其实大家高中的时候都学过的，求解坐标系里两个函数交汇的区域的极值之类的题目），多层的神经网络也很类似于线性规划，至少在二元三元平面上看是类似的，都是通过一条条线或者一个个面去划分一个区域进行分类。如下图

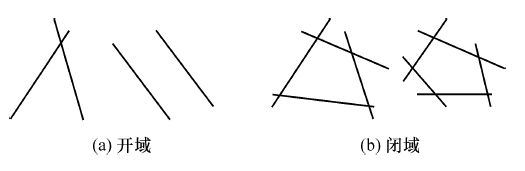
线性规划的边都是直的，所以面对非线性分布的样本，也就是样本的边边是弯的，那这时候就需要加入一个东西，把原先的线性规划，变成非线性规划，说白了，就是本来用直线去分割空间的方法改用曲线去分割空间。曲线的水太深，从定义域到值域，都增加了想象和推导的难度。所以用什么样的曲线好呢，这就是一个值得去研究的问题了，在这里不做展开。我们按常规的几种吧，就是sigmoid函数，也就是逻辑回归的那条线。

def sigmoid(z):
    return 1/(1+math.exp(-z))#这就是个标准sigmoid函数

用这个做激活函数，也就是把线性规划变成非线性规划的关键。把分割直线变成曲线以后，效果是啥样的，大家可以想象一下，图没找着。

好了模型分类原理大概就是这样，接下来的问题就是如何去解这么一个模型的参数。
想要自己求解这个模型，首先你得有以下数学基础。

1. 求导能力，想来大家高中的时候都经历过的。
2. 复合函数的求导能力，f(g(x)) = f’(g(x))*g’(x)，都是高中基本功。
3. 理解偏导数。其实偏导数就是看起来很难的一元求导。看起来一个很复杂的多元函数，你把其他元都当成常数按需求导就完事了。并不难。
4. 理解一下一阶泰勒展开到牛顿法，如何去通过逼近求解一个方程根的问题。这个是关键。梯度其实就是根据一阶导数的方向变化去逼近导数最极值的点。推荐去看一下《数值分析》清华大学出的一本大学教材，里面有详细的描述整个过程。

如果你没耐心去学习上述内容，那么，求解对于你来说也是扯淡。
好了接下来我们求一下吧：(作图敲公式懒得，手写拍一下得了。)
在这里插入图片描述


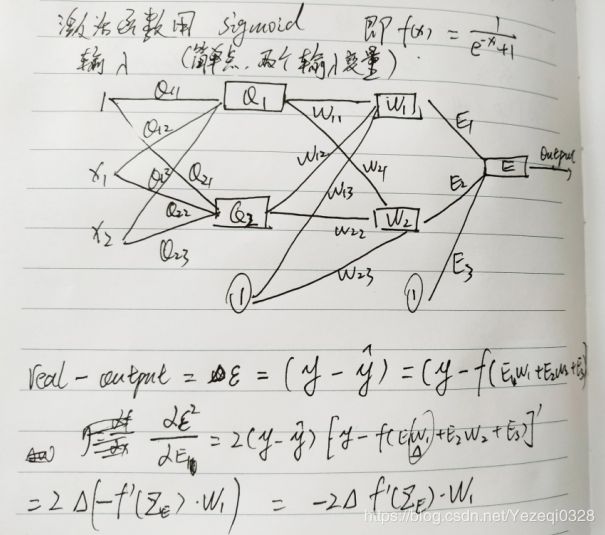
字有些丑陋，但是推导的重点我已经圈起来了。看起来有点复杂的推导，实际上就是一个很基础的复合函数求导法则以及简单偏导数的应用。
至于为什么要求误差对于参数的偏导数，这就是梯度下降法的关键所在，根据导数的变化来决定迭代变化，引入η学习率来调节参数迭代的变化。求得对应的偏导数，那么参数的迭代变化也就很显然了：

可是众所周知，这样确定迭代率的梯度下降法，并不优秀，甚至有时候会训练成人工智障。所以参考了韩力群教授的《人工神经网络教程》里面介绍的几种优化方法，这里我选取了一种。如下：
标准BP 算法在调整权值时，只按t 时刻误差的梯度降方向调整，而没有考虑t 时刻以前的梯度方向，从而常使训练过程发生振荡，收敛缓慢。为了提高网络的训练速度，可以在权值调整公式中增加一动量项。若用W 代表某层权矩阵，X代表某层输入向量，则含有动量项的权值调整向量表达式为
ΔW（t） ＝ η δX ＋ αΔW（t － １） （３ ．２９）
可以看出，增加动量项即从前一次权值调整量中取出一部分叠加到本次权值调整量中，α 称为动量系数，一般有α ∈ （０ ，１） 。动量项反映了以前积累的调整经验，对于t 时刻的调整起阻尼作用。当误差曲面出现骤然起伏时，可减小振荡趋势，提高训练速度。

开搞

既然参数的迭代变化已经求出来了，那就可以开始整理思路敲代码了。
首先测试数据我这里就不多做交代了，随便吧。
总之第一步，先连接数据库，把初始参数存进去，然后在程序一开始把初始参数拿来迭代，并在迭代结束后，存储迭代后的参数。
首先我所遭遇的问题就是误差的求取。对于一次简单的二分类，即0，1分类，我们采用simoid激活函数，那么我们最好得到的输出会是在【0,1】之间的一个数，于是我规定，凡大于0.5的分类为1，小于等于0.5的分类为0。那么当分类本应为0时，算法判断为1，那么说明输出 y>0.5 所以就有了一个最小误差 >= ( 0.5 - y ) 这样就可以获得误差进入迭代。
而最小误差毕竟是最小误差，所以我加入了一个新的规则，就是每次迭代样本每多错一次，就增加一点误差作为惩罚。增加到最后这个样本每次错了都会用最大误差进入迭代。（关于这个，我本身并没有去推导过，但是直觉告诉我这样做没错。）
有了误差了，接下来就可以开始写程序了：

定义一些函数：

# 逻辑回归函数用于激活神经元
def sigmoid(z):
    return 1/(1+math.exp(-z))
# 逻辑回归函数的一阶导数
def DeltaSigmoid(z):
    return sigmoid(z)*(1-sigmoid(z))
# 分类规则，sigmoid激活输出神经元输出(0,0.5]为 0， (0.5,1) 为 1
def sign(z):
    if z<=0.5:
        return 0
    else:
        return 1
# 神经网络计算函数，返回各个层的输出值和激活函数的输出值
def doNeural(data,params):
    data.append(1)
    #第一层三个神经元计算
    sumOne = [] #第一层单个神经元的输出(求和的)
    sigOne = [] #第一层单个神经元经过激活函数变换的输出值
    for i in range(0,3):
        s = np.array(data).dot(np.array(params['w_1'][i]))
        sumOne.append(s)
        sigOne.append(sigmoid(s))
    #第二层两个神经元
    sumTwo = []
    sigTwo = []
    useSigInput = sigOne
    useSigInput.append(1)
    for i in range(0,2):
        s = np.array(useSigInput).dot(np.array(params['w_2'][i]))
        sumTwo.append(s)
        sigTwo.append(sigmoid(s))
    #输出层一个神经元
    sumThree = []
    sigThree = []
    useSigInput= sigTwo
    useSigInput.append(1)
    s = np.array(useSigInput).dot(np.array(params['w_3'][0]))
    sumThree.append(s)
    sigThree.append(sigmoid(s))
    del data[-1]
    return [sumOne,sigOne,
            sumTwo,sigTwo,
            sumThree,sigThree]
# 设定对应样本值所对应的激活函数的期望输出ExpectSigmoid
def getExpect(realY):
    if realY==0:#我用二八开，这个可以调整。就是迭代中的迭代临界值。
        return 0.2
    else:
        return 0.8
# 计算权值的调整量
def DeltaForParams(ExpectSigmoid, result, oldparams, data, yita = 0.1):#这里yita的默认值为0.1
    #权值的调整是从输出层调节到输入层。
    data.append(1)
    DeltaWOne = np.zeros(np.array(oldparams['w_1']).shape)#初始化一个矩阵用来存储输入层的参数调整值
    params = oldparams
    for i in range(0,3):
        Error = ExpectSigmoid - result[5][0]
        Delta = result[5][0]*(1-result[5][0])
        w_3 = params['w_3'][0][i]
        DeltaParams['w_3'][0][i] = yita*Error*Delta*result[3][i] + yita*0.5*DeltaParamsOld['w_3'][0][i] #当前的梯度加上上一次的梯度的一部分，即动量项。
        DeltaParamsOld['w_3'][0][i] = DeltaParams['w_3'][0][i] #将本次迭代中的梯度存储，下次迭代用
        if i < 2:
            for j in range(0,4):
                w_2 = params['w_2'][i][j]
                DeltaParams['w_2'][i][j] = yita*Error*Delta*w_3*DeltaSigmoid(result[2][i])*result[1][j] + 0.5*yita*DeltaParamsOld['w_2'][i][j]
                DeltaParamsOld['w_2'][i][j] = DeltaParams['w_2'][i][j]
                if j < 3:
                    for k in range(0,7):
                        DeltaWOne[j][k] = DeltaWOne[j][k] + yita*Error*Delta*w_3*DeltaSigmoid(result[2][i])*w_2*DeltaSigmoid(result[0][j])*data[k]
    for ii in range(0,3):
        for jj in range(0,7):
            DeltaParams['w_1'][ii][jj] = DeltaWOne[ii][jj] + 0.5*yita*DeltaParamsOld['w_1'][ii][jj]
            DeltaParamsOld['w_1'][ii][jj] = DeltaParams['w_1'][ii][jj]
    del data[-1]
    return DeltaParams

这里就包括了核心的权值调整函数DeltaForParams，默认的学习率我设置为0.1
其他函数我都注释到代码里了，就不再解释。

最后进行计算：

#---------------------------开始迭代----------------------------------------
goNumber = 1 #迭代次数
yita = 0.5 #yita 学习率
oldTrue = 0 #上一次迭代的整体样本分类正确率
ErrorSampleIndex = [] #存储计算中的异常样本点

while 1:
    for i in range(0,len(inputData)):
        result = doNeural(inputData[i], StratParams)#计算样本
        getReY = sign(result[5][0])#获取分类
        cishu = 1 #单样本迭代次数
        ExpectSigmoid = getExpect(forInputY[i])#获取对应的激活函数的期望输出
        while (abs(ExpectSigmoid - result[5][0]) >= 0.01):#不管分类正确与否，只看网络与期望值得误差，只要误差小于阈值都进入迭代。(阈值可变)
            if getReY == forInputY[i]: #如果在分类正确的情况下激活函数输出在[0.2,0.8]以外的样本点不进行循环计算
                # （这个边界的确定值有待考量）
                if getReY == 1 and result[5][0] >= 0.8:
                    break
                if getReY == 0 and result[5][0] <= 0.2:
                    break
            #将计算好的权值的调整量存入预先设定好的DeltaParams中
            DeltaParams = DeltaForParams(ExpectSigmoid, result, StratParams, inputData[i], yita)
            #调整参数
            for ii in range(0,len(StratParams['w_3'][0])):
                StratParams['w_3'][0][ii] = DeltaParams['w_3'][0][ii] + StratParams['w_3'][0][ii]
            for ii in range(0,len(StratParams['w_2'])):
                for jj in range(0,len(StratParams['w_2'][0])):
                    StratParams['w_2'][ii][jj] = StratParams['w_2'][ii][jj] + DeltaParams['w_2'][ii][jj]
            for ii in range(0,len(StratParams['w_1'])):
                for jj in range(0,len(StratParams['w_1'][0])):
                    StratParams['w_1'][ii][jj] = StratParams['w_1'][ii][jj] + DeltaParams['w_1'][ii][jj]
            #重新计算网络的输出
            result = doNeural(inputData[i], StratParams)
            print("\r第 %d 次迭代中，第 %d 个样本的 %d 次循环迭代!"%(goNumber,i+1,cishu),end="",flush=True)
            cishu = cishu + 1
            if cishu > 10000 or (i in ErrorSampleIndex):#防止单样本无法收敛，使得迭代无限循环在这个样本里。
                print(inputData[i], i)#如果有单样本无法收敛，输出该样本并标记为异常点，以后遇见它不再迭代
                ErrorSampleIndex.append(i)
                break
    trueResult = 0 #本次参数调整后正确的分类结果计数
    for i in range(0,len(inputData)):
        result = doNeural(inputData[i], StratParams)
        getReY = sign(result[5][0])
        if getReY == forInputY[i]:
            trueResult = trueResult + 1 #如果分对了 就加1
    zhengquelv = trueResult/(len(inputData)-len(ErrorSampleIndex)) #计算正确率,计算正常样本点的分类正确率
    print('第 %d 次迭代, 本次迭代正确率 %.2f'%(goNumber, zhengquelv))#打印本次迭代的对应结果
    print(StratParams['w_3'], trueResult, yita)
    if abs(zhengquelv - oldTrue) <= 0.001: #控制迭代中的yita
        yita = yita * 1.01    # 如果迭代后，结果变化缓慢，增加yita值，我设的是增少减多的保守迭代，(可改)
        if yita >= 0.99:#防止无限增加
            yita = 0.9
    if abs(zhengquelv - oldTrue) >= 0.01:
        yita = yita * 0.9  #如果迭代后，结果变化剧烈，则减小yita值
        if yita <=0.02: #防止无限减小
            yita = 0.1
    oldTrue = zhengquelv
    if trueResult/len(inputData) > 0.90:#设置迭代终止条件，即分类正确率达标。(目前为止最高正确率0.94)
        mongo = mongo_data()#将达标后的神经网络参数存入服务器
        print(mongo.Neural_set_params(StratParams, name='NeuralBP_params'))#参数存储为服务器上的'NeuralBP_params'数据集
        break
    goNumber = goNumber + 1#总的迭代次数加一
# -------------------------------------迭代结束------------------------------------

#比较网络预测值和真实值的吻合情况
print("预测值：")
yuce = []
for d in data_x[140:]:
    result = doNeural(d, StratParams)
    yuce.append(sign(result[5][0]))
print(yuce)

print("真实值：")
print(data_y[140:])
#计算样本吻合率。
countTrue = 0
realSample = data_y[140:]
for i in range(0,len(yuce)):
    if yuce[i] == realSample[i]:
        countTrue = countTrue+1 #算对了的，加一
print("样本吻合率：%.2f"%(countTrue/len(yuce)))

计算结果

我这次写的算法，针对一百四十个样本，分类正确率只能达到95.4%，并没有达到我的期望值，不过我对神经网络的研究还处于表面，接下来会去思考学习如何让我的人工智障变成真正的人工智能，去面对更加复杂的情形。这会很有意思。