skiplist跳表的 实现

前言

rocksdb 的memtable中默认使用跳表数据结构对有序数据进行的管理，为什么呢？

同时redis 也用跳表作为管理自己有序集合的数据结构，为什么他们不选择用红黑树来管理(同样能够提供高效的插入，查找，删除操作，而且各种语言都已经封装好了很多轮子),就选择跳表来实现？

今天就来仔细探讨一下这个数据结构。

跳表结构

对于一个单链表来说，即使链表中存储的数据结构是有序的，想要查找一个元素也需要从头到尾进行查找，时间复杂度是O(n)。

提高查效率的一种办法就是建立索引，对链表建立一级索引，每两个节点提取一个索引节点到上一级，把抽取出来的一级叫做索引。如下图，down就是索引节点指向节点的指针:

此时如果我们想要查找某个节点，比如18。可以先在索引层遍历，当遍历到索引层节点值为13时，发现没有next指针了，此时下降到原始节点层，继续遍历。这个时候只需要遍历一个节点就能访问到数值为18的节点了。

这样的话原来要找节点18，需要遍历8个节点，此时只需要遍历6个节点了，查找效率提高了。那如果我们再增加一级索引，效率会不会更高呢？还是在第一级索引节点的基础上再创建一级索引，如下图：

在查找部分节点的情况下效率能够更高，因为这里举例的数据量较小，查看如下数据，有64个原始节点，按照如上的思路建立了五级索引。

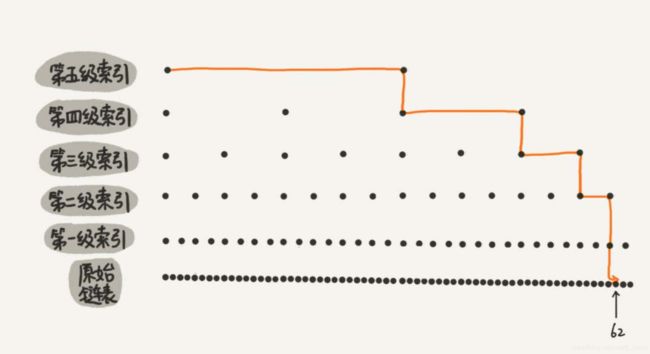
此时查找节点62，原始链表需要遍历62个节点，此时只需要遍历11个节点即可访问到，在数据量较为庞大的情况下效率提升非常明显。

时间复杂度

单链表中查找一个节点的效率是O(n)，那么跳表中查找一个节点的时间复杂度是多少呢？
按照我们上面所说，每两个原始节点抽取为一个索引节点的思路。

假设现在有n个节点，每两个节点抽取一个索引节点，那么第一级索引节点的个数：n/2，第二级索引节点：n/4，第三节索引节点：n/8，依次第k级索引节点：n/(2^k)

假设索引有h级，最高级的索引有2个结点。通过上面的公式，我们可以得到n/(2h)=2，从而求得h=log2n-1。如果包含原始链表这一层，整个跳表的高度就是log2n。
我们在跳表中查询某个数据的时候，如果每一层都要遍历m个结点，那在跳表中查询一个数据的时间复杂度就是O(m*logn)。

如何确定m的数值是多少呢，按照上面的索引结构，从最顶层的索引层开始遍历一直到最底层，每一级索引最多需要遍历3个节点。
证明如下：

• 假设我们要查找的数据是x，在第k级索引中
• 遍历到y结点之后，发现x大于y，小于后面的结点z，所以我们通过y的down指针，从第k级索引下降到第k-1级索 引
• 在第k-1级索引中，y和z之间只有3个结点(包含y和z),即我们在K-1级索引中最多只需要遍历3个结点，依次类推，每一级索引都最多只需要遍历3个结 点。

所以我们可以得到m=3这样的一个结论，则在跳表中查询任意一个节点的时间复杂度都为O(logn)，效率和二分查找一样。

但是问题也很明显，索引节点消耗内存空间，这是以空间换时间的方式来达到优化的目的，接下来我们看看空间的消耗

空间复杂度

假设原始链表大小为n,我们前面也说过之上的索引节点的个数依次为：
第一级索引节点的个数：n/2，第二级索引节点：n/4，第三节索引节点：n/8，依次第k级索引节点：n/(2^k)，直到剩下两个索引节点

这几级索引节点的总和：n/2 + n/4 + n/8 +… 8 + 4 +2 = n -2
可以看出跳表的空间复杂度是O(n)。也就是说，如果将包含n个结点的单链表构造成跳表，我们需要额外再用 接近n个结点的存储空间。那我们有没有办法降低索引占用的内存空间呢?

之前我们是每两个节点抽取一个索引节点，同样我们可以每三个节点抽取一个索引节点，示意图如下：

依次总的索引节点的个数为：n/3 + n/9 + n/27 +… + 9 + 3 = n /2
虽然还是O(n)的空间复杂度，但是整体比上面的抽取方式少占用一般的空间。且实际开发过程中，原始链表中存储的大都是数据量庞大的数据，索引节点仅仅存储一些关键数据以及指针，基本的空间消耗并不会很大，可以忽略不计得。

高效的动态插入和删除

插入数据和查找数据的时间复杂度一样，单链表的插入性能消耗O(n)在查找插入位置上，而真正的插入只需要O(1)的时间。同样，跳表的插入也是消耗在查找的时间复杂度上O(logn)。

删除的时候，我们在找到原始链表中的节点之后，如果该节点还出现在索引节点之中，我们除了要删除原始链表中的节点，还需要删除索引层中的节点。

跳表索引的动态更新

当我们不停地往跳表中插入数据时，如果我们不更新索引，就有可能出现某2个索引结点之间数据非常多的情况。极端情况下，跳表还会退化成单链表。
如下这种情况：

红黑树、AVL树这样平衡二叉树，它们是通过左右旋的方式保持左右子树的大小平衡(如果不了解也没关系，我们后面会讲)，而跳表是通 过随机函数来维护前面提到的“平衡性”。

过程如下：

• 通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了K
• 查找当前节点要插入的原始节点的位置
• 基于该位置,从原始链表层向上，每层建立一个指向该节点的down指针，直到第K层
  如下节点6 插入该跳表，并且随机函数生成的K=2，即对6创建索引节点直到第二层
  

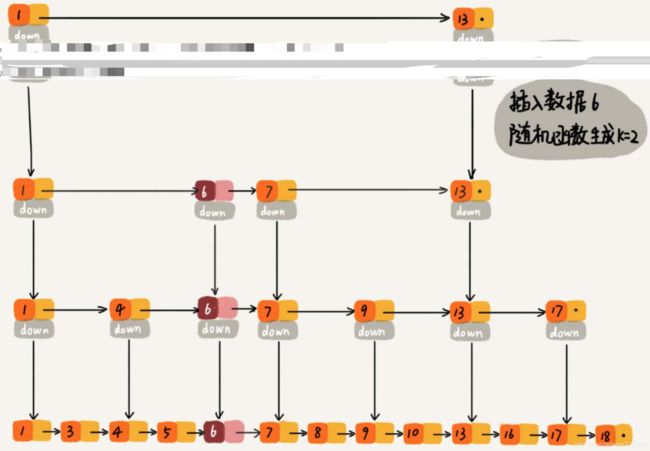
总结

综上描述，我们了解了跳表的查找，插入，删除，更新的过程，为什么rocksdb和redis都想要使用跳表作为自己的有序集合的管理结构呢？

像redis和rocksdb 都提供以下核心的数据操作：

• 插入一个数据
• 删除一个数据
• 查找一个数据
• 查找一个区间数据[52,100]
• 不断输出一个有序序列

以上插入，查找，删除，迭代输出的操作跳表和红黑树的效率接近，但是range查找则红黑树没有跳表高
在区间查找的时候，跳表只需要找到区间的第一个元素即可顺序遍历即可（元素是有序的），但是红黑树每一个元素都需要相同的复杂度。

但是跳表并没有红黑树的接口通用，很多语言都提供红黑树的实现接口，跳表还需要自己实现。

详细实现

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

/**
 * 跳表的一种实现方法。
 * 跳表中存储的是正整数，并且存储的是不重复的。
 * 
 *  跳表结构:
 * 
 *  第K级           1           9
 *  第K-1级         1     5     9
 *  第K-2级         1  3  5  7  9
 *  ...             ....
 *  第0级(原始链表)  1  2  3  4  5  6  7  8  9
 */

const int MAX_LEVEL = 16;

/**
 * @brief 节点
*/
class CNode
{
public:
    CNode();
    ~CNode();

    std::string toString();
    /**
     * @brief 获取索引链表
    */
    CNode** GetIdxList();

    /**
     * @brief 设置数据
    */
    void SetData(int v);
    /**
     * @brief 获取数据
    */
    int GetData();
    /**
    * @brief 设置最大索引级别
    */
    void SetLevel(int l);
private:
    /**当前节点的值*/
    int m_data;
    /** 
     * 当前节点的每个等级的下一个节点.
     * 第2级 N1 N2
     * 第1级 N1 N2
     * 如果N1是本节点,则 m_lpForwards[x] 保存的是N2
     * 
     * [0] 就是原始链表.
     */
    CNode* m_lpForwards[MAX_LEVEL];
    /**当前节点的所在的最大索引级别*/
    int m_iMaxLevel;
};

/**
 * @brief 跳表
*/
class CSkipList
{
public:
    CSkipList();
    ~CSkipList();
    /**
     * @brief 查找指定的值的节点
     * @param v 正整数
    */
    CNode* Find(int v);
    /**
     * @brief 插入指定的值
     * @param v 正整数
    */
    void Insert(int v);
    /**
     * @brief 删除指定的值的节点
     * @param v 正整数
    */
    int Delete(int v);
    void PrintAll();
    /**
     * @brief 打印跳表结构
     * @param l 等于-1时打印所有级别的结构 >=0时打印指定级别的结构
    */
    void PrintAll(int l);
    /**
     * @brief 插入节点时,得到插入K级的随机函数
     * @return K
    */
    int RandomLevel();

private:
    int levelCount;
    /**
     * 链表
     * 带头/哨所(节点)
    */
    CNode* m_lpHead;
};

int main()
{
    CSkipList skipList;
    /// 插入原始值
    for(int i=1; i< 50; i++){
        if((i%3) == 0){
            skipList.Insert(i);
        }
    }
    for(int i=1; i< 50; i++){
        if((i%3) == 1){
            skipList.Insert(i);
        }
    }
    skipList.PrintAll();
    std::cout<<std::endl;
    // 打印所有等级结构
    skipList.PrintAll(-1);
    // 查找
    std::cout<<std::endl;
    CNode* lpNode = skipList.Find(27);
    if(NULL != lpNode){
        std::cout<<"查找值为27的节点,找到该节点,节点值:"<<lpNode->GetData()<<std::endl;
    }else{
        std::cout<<"查找值为27的节点,未找到该节点"<<std::endl;
    }
    /// 删除
    std::cout<<std::endl;
    int ret = skipList.Delete(46);
    if(0 == ret){
        std::cout<<"查找值为46的节点,找到该节点,并删除成功"<<std::endl;
    }else{
        std::cout<<"查找值为46的节点,找到该节点,删除失败"<<std::endl;
    }
    std::cout<<std::endl;
    //打印所有等级结构
    skipList.PrintAll(-1);
    std::cin.ignore();
    return 0;
}

CNode::CNode()
{
    m_data = -1;
    m_iMaxLevel = 0;
    for(int i=0; i<MAX_LEVEL; i++){
        m_lpForwards[i] = NULL;
    }
}
CNode::~CNode()
{

}
CNode** CNode::GetIdxList()
{
    return m_lpForwards;
}

void CNode::SetData(int v)
{
    m_data = v;
}
int CNode::GetData()
{
    return m_data;
}
void CNode::SetLevel(int l)
{
    m_iMaxLevel = l;
}
std::string CNode::toString()
{
    char tmp[32];
    std::string ret;

    ret.append("{ data: ");
    sprintf(tmp, "%d", m_data);
    ret.append(tmp);
    ret.append("; levels: ");
    sprintf(tmp, "%d", m_iMaxLevel);
    ret.append(tmp);
    ret.append(" }");
    return ret;
}

CSkipList::CSkipList()
{
    levelCount = 1;
    m_lpHead = new CNode();
}
CSkipList::~CSkipList()
{

}
CNode* CSkipList::Find(int v)
{
    CNode* lpNode = m_lpHead;
    /**
     * 从 最大级索引链表开始查找.
     * K -> k-1 -> k-2 ...->0
    */
    for(int i=levelCount-1; i>=0; --i){
        /**
         * 查找小于v的节点(lpNode).
        */
        while((NULL != lpNode->GetIdxList()[i]) && (lpNode->GetIdxList()[i]->GetData() < v)){
            lpNode = lpNode->GetIdxList()[i];
        }
    }
    /**
     * lpNode 是小于v的节点, lpNode的下一个节点就等于或大于v的节点
    */
    if((NULL != lpNode->GetIdxList()[0]) && (lpNode->GetIdxList()[0]->GetData() == v)){
        return lpNode->GetIdxList()[0];
    }
    return NULL;
}
void CSkipList::Insert(int v)
{
    /// 新节点
    CNode* lpNewNode = new CNode();
    if(NULL == lpNewNode){
        return;
    }

    /**
     * 新节点最大分布在的索引链表的上限
     * 如果返回 3,则 新的节点会在索引1、2、3上的链表都存在
    */
    int level = RandomLevel();
    lpNewNode->SetData(v);
    lpNewNode->SetLevel(level);

    /**
     * 临时索引链表
     * 主要是得到新的节点在每个索引链表上的位置
    */
    CNode *lpUpdateNode[level];
    for(int i=0; i<level; i++){
        /// 每个索引链表的头节点
        lpUpdateNode[i] =m_lpHead;
    }
    CNode* lpFind = m_lpHead;
    for(int i= level-1; i >= 0; --i){
        /**
         * 查找位置
         *   eg.  第1级  1  7  10
         *   如果插入的是 6
         *   lpFind->GetIdxList()[i]->GetData() : 表示节点lpFind在第1级索引的下一个节点的数据
         *   当 "lpFind->GetIdxList()[i]->GetData() < v"不成立的时候,
         *   新节点就要插入到 lpFind节点的后面, lpFind->GetIdxList()[i] 节点的前面
         *   即在这里 lpFind就是1  lpFind->GetIdxList()[i] 就是7
        */
        while((NULL != lpFind->GetIdxList()[i]) && (lpFind->GetIdxList()[i]->GetData() < v)){
            lpFind = lpFind->GetIdxList()[i];
        }
        /// lpFind 是新节点在 第i级索引链表的后一个节点
        lpUpdateNode[i] = lpFind;
    }

    for(int i=0; i<level; ++i){
        /**
         * 重新设置链表指针位置
         *   eg  第1级索引 1  7  10
         *      插入6.
         *      lpUpdateNode[i] 节点是1; lpUpdateNode[i]->GetIdxList()[i]节点是7
         *  
         *  这2句代码就是 把6放在 1和7之间
        */
        lpNewNode->GetIdxList()[i] = lpUpdateNode[i]->GetIdxList()[i];
        lpUpdateNode[i]->GetIdxList()[i] = lpNewNode;
    }
    if(levelCount < level){
        levelCount = level;
    }
}
int CSkipList::Delete(int v)
{
    int ret = -1;
    CNode *lpUpdateNode[levelCount];
    CNode *lpFind = m_lpHead;
    for(int i=levelCount-1; i>= 0; --i){
        /**
         * 查找小于v的节点(lpFind).
        */
        while((NULL != lpFind->GetIdxList()[i]) && (lpFind->GetIdxList()[i]->GetData() < v)){
            lpFind = lpFind->GetIdxList()[i];
        }
        lpUpdateNode[i] = lpFind;
    }
    /**
     * lpFind 是小于v的节点, lpFind的下一个节点就等于或大于v的节点
    */
    if((NULL != lpFind->GetIdxList()[0]) && (lpFind->GetIdxList()[0]->GetData() == v)){
        for(int i=levelCount-1; i>=0; --i){
            if((NULL != lpUpdateNode[i]->GetIdxList()[i]) && (v == lpUpdateNode[i]->GetIdxList()[i]->GetData())){
                lpUpdateNode[i]->GetIdxList()[i] = lpUpdateNode[i]->GetIdxList()[i]->GetIdxList()[i];
                ret = 0;
            }
        }
    }
    return ret;
}
void CSkipList::PrintAll()
{
    CNode* lpNode = m_lpHead;
    while(NULL != lpNode->GetIdxList()[0]){
        std::cout<<lpNode->GetIdxList()[0]->toString().data()<<std::endl;
        lpNode = lpNode->GetIdxList()[0];
    }
}
void CSkipList::PrintAll(int l)
{
    for(int i=MAX_LEVEL-1; i>=0;--i){
        CNode* lpNode = m_lpHead;
        std::cout<<"第"<<i<<"级:"<<std::endl;
        if((l < 0) || ((l >= 0) && (l == i))){
            while(NULL != lpNode->GetIdxList()[i]){
                std::cout<<lpNode->GetIdxList()[i]->GetData()<<" ";
                lpNode = lpNode->GetIdxList()[i];
            }
            std::cout<<std::endl;
            if(l >= 0){
                break;
            }
        }
    }
}
int GetRandom()
{
    static int _count = 1;
	std::default_random_engine generator(time(0) + _count);
	std::uniform_int_distribution<int> distribution(1,99999/*0x7FFFFFFF*/);
	int dice_roll = distribution(generator);
    _count += 100;
	return dice_roll;
}
int CSkipList::RandomLevel()
{
    int level = 1;
    for(int i=1; i<MAX_LEVEL; ++i){
        if(1 == (GetRandom()%3)){
            level++;
        }
    }
    return level;
}