数据结构—线性表的顺序存储结构实现与分析
文章向导
线性表及顺序存储结构
各部分接口的实现
完整的验证实例
插入、删除操作的算法时间复杂度
一、线性表及顺序存储结构
线性表即有限个数据元素的序列,而其顺序存储结构则指的是用一段地址连续的存储单元依次存储线性表中的数据。在高级语言中(如C语言)一般可用一维数组来实现顺序存储结构。
二、各部分接口的实现
定义在一个线性表上的操作有许多,比如初始化、清空、读/写、查找定位、插入/删除等。对于不同的应用,线性表的基本操作是不同的,但对于实际问题中所涉及到的复杂操作,基本上都是由这些基本操作来组合实现。
这里主要讲解读写、插入、删除三种基本操作的算法实现,现在先在头文件中给出其抽象数据类型的定义。
#ifndef SQLIST_H
#define SQLIST_H
#include 1.获取元素操作
获取线性表L中某个位置的元素值。
算法思路:
- 若未创建线性表或查找位置不合理,则抛出异常;
- 将查找位置对应的数组元素返回给变量e 。
/* 函数名:sqlist_get_elm
*
* 功能:获取顺序线性表中第get_loc个位置处的元素值(用e返回)
*
* 入口参数:
* > list: 整个顺序线性表
* > get_loc: 待查找的位置
* > e: 查找后返回的值
*
* 返回值:-1: fail, 0: success
*/
int sqlist_get_elm(SqList list, int get_loc, ElemType* e)
{
/*输入参数检查*/
if (get_loc < 1 || get_loc > list.length) {
printf("get_loc err!\n");
return -1;
} else {
*e = list.data[get_loc-1]; //查找位置与数组下标的关系
return 0;
}
}
读者阅读时可思考下接口sqlist_get_elm的第一个参数定义为SqList* list与定义为SqList list的区别,以及第三个参数定义为ElemType* e与ElemType e的区别。
2.插入元素操作
在线性表L中的第i个位置插入新元素e。
算法思路:
- 若插入位置不合理,则抛出异常;
- 若线性表长度大于数组存储长度,则抛出异常或动态增加容量(本例为抛出异常);
- 从表尾元素开始向前遍历到第i个位置,然后将它们都向后移动一个位置;
- 将要插入元素填入位置i处;
- 表长加1
/* 函数名:sqlist_ins_elm
*
* 功能:在顺序线性表中第ins_loc个位置插入元素
*
* 入口参数:
* > list: 整个顺序线性表
* > ins_loc: 待插入的位置
* > e: 待插入的元素值
*
* 返回值:-1: fail, 0: success
*/
int sqlist_ins_elm(SqList* list, int ins_loc, ElemType e)
{
int i;
if (list->length == MAXSIZE) {
printf("list is crowed!\n");
return -1;
}
/*使用list->length+1是考虑到插入表尾时的情况*/
if (ins_loc < 1 || ins_loc > (list->length + 1)) {
printf("ins_loc err!\n");
return -1;
}
if (ins_loc <= list->length) { /*若插入数据位置不在表尾*/
/*list->length-1为位置与下标的关系
*ins_loc-1也为位置与下标的关系, 同时也是作为从表尾遍历到第ins_loc个位置的判据
*/
for (i = list->length - 1; i >= ins_loc - 1; i--) {
list->data[i+1] = list->data[i]; //将要插入位置后的数据元素均向后移动一位
}
}
list->data[ins_loc-1] = e; //将新元素插入
list->length++;
return 0;
}
3.删除操作
删除线性表L中第i个位置的元素,并用变量e返回删除的值。
算法思路:
- 若删除位置不合理,则抛出异常;
- 取出删除元素;
- 从删除元素位置遍历至最后一个元素的位置,分别将它们向前移动一个位置;
- 表长减1
/* 函数名:sqlist_del_elm
*
* 功能:删除顺序线性表中第del_loc个位置的元素
*
* 入口参数:
* > list: 整个顺序线性表
* > del_loc: 待插入的位置
* > e: 返回删除位置后面一个位置的元素
*
* 返回值:-1: fail, 0: success
*/
int sqlist_del_elm(SqList* list, int del_loc, ElemType* e)
{
int i;
/*删除位置检查*/
if (del_loc<1 || del_loc>list->length) {
printf("del_loc err!\n");
return -1;
}
*e = list->data[del_loc]; //用e返回待删除元素的后一个位置的元素值
//若删除的位置不是表尾
if (del_loc < list->length) {
/*将删除位置处的后继元素前移*/
for (i=del_loc; i<list->length; i++) {
list->data[i-1] = list->data[i]; //注意理解位置与下标的关系
}
}
list->length--; //删除为表尾时的偷懒处理
return 0;
}
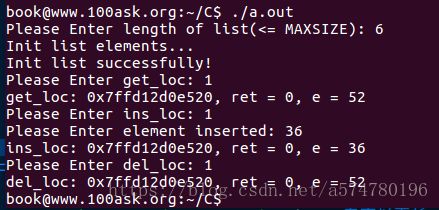
三、完整的测试实例
#include 四、算法时间复杂度的分析
由“获取元素操作”的示例可知,线性表的顺序存储结构在读、写操作时,不论是哪个位置其时间复杂度都为O(1)。而插入或删除时,因为程序的执行次数取决于问题的输入规模(即Ins_Loc或Del_Loc的值),程序的直接体现则为for循环的执行次数。下面具体分析插入、删除元素是的时间复杂度。
1.插入操作的时间复杂度
假定在任意位置插入元素的概率Pi相等: (表长为n,n+1个位置)
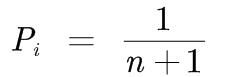
元素插入位置的可能值:i=1,2,3, … ,n, n+1
相应的移动次数:(n-i+1) = n,n-1, … ,1,0
由概率论中数学期望的观点可得平均移动次数:
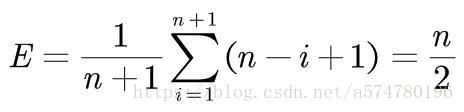
最后由时间复杂度的推导可知,插入操作的平均时间复杂度为O(n)。
为何要分析平均移动次数呢?因为插入位置的不同,移动次数自然也不同,而考虑最坏或最好的情况都不具有代表性,自然应分析平均情况。
2.删除操作的时间复杂度
假定在线性表中的任意位置删除元素的概率相等:(表长为n,n个位置)
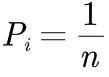
元素删除位置的可能值:i=1,2,…,n
相应向前移动的次数:(n-i)=n-1,n-2,…,0
由概率论中数学期望的观点可得平均移动次数:

最后由时间复杂度的推导可知,删除操作的平均时间复杂度也为O(n)。
参阅资料
大话数据结构
算法精解—C语言描述
http://www.docin.com/p-1723299970.html