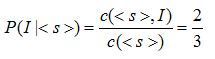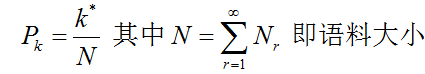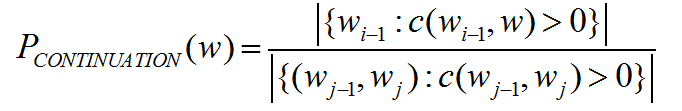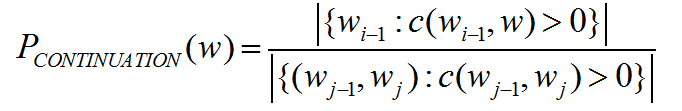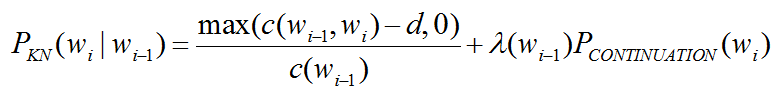Statistical language model 统计语言模型
学习笔记来自斯坦福公开课的自然语言处理(https://class.coursera.org/nlp/),以其中讲义为主,加入自己的学习理解,以加深学习印象。
内容提纲:
1. N-GRAM介绍
2. 参数估计
3. 语言模型的评价
4. 数据稀疏问题
5. 平滑方法
N-GRAM介绍
现在很多的应用中,需要计算一个句子的概率,一个句子是否合理,就看看它的可能性大小,这里可能性的大小就用概率来衡量。比如下面几个例子:
- 在机器翻译中:
P(high winds tonite) > P(large winds tonite)
- 拼写检查中:
比如这一句话:The office is about fiIeen minuets from my house
显然 P(about fiIeen minutes from) > P(about fiIeen minuets from)
- 语音识别中:
比如I saw a van 和eyes awe of an听上去差不多,但是P(I saw a van) >> P(eyes awe of an)
上面的几个例子中都需要计算一个句子的概率,以作为判断其是否合理的依据。下面将上述的内容形式化描述。
我们需要计算一个句子或序列W的概率: P(W) = P(w 1 ,w 2 ,w 3 ,w 4 ,w 5 …w n )
其中我们也需要计算一个相关的任务,比如P(w 5 |w 1 ,w 2 ,w 3 ,w 4 ),表示w 1 w 2 w 3 w 4 后面是w 5的概率,即下一个词的概率。
像这样计算P(W)或者P(w n |w 1 ,w 2 …w n-‐1 ) 的模型叫做语言模型( language model简称LM)。
那么如何计算P(W)呢?用概率的链式规则,链式规则常常用来评估随机变量的联合概率,链式规则如下:
将上面的链式规则计算P(W)可以写作如下:
按照链式规则计算方式,举例如下:
P(“its water is so transparent”) = P(its) × P(water|its) × P(is|its water) × P(so|its water is) × P(transparent|its water is so)
那么下面的问题是如何计算上面每一个概率,比如 P(transparent|its water is so),一种比较直观的计算就是计数然后用除法:
事实上不能用这种方式去计算条件概率,原因有两个:
1.直接这样计算会导致参数空间过大,一个语言模型的参数就是所有的这些条件概率,试想按上面方式计算P(w 5 |w 1 ,w 2 ,w 3 ,w 4 ),这里w i都有一个词典大小取值的可能,记作|V|,则该模型的参数个数是|V|^5,而且这还不包含P(w 4 | w1, w2, w3)的个数,可以看到这样去计算条件概率会使语言模型参数个数过多而无法实用。
2.数据稀疏严重,我的理解是像上面那样计数计算,比如计数分子its water is so transparen,在我们所能见的文本中出现的次数是很小的,这样计算的结果是过多的条件概率会等于0,因为我们根本没有看到足够的文本来统计!
上面的计算方式是通过马尔科夫假设进行简化的,马儿可夫假设是指假设第wi个词语只与它前面的k个词语相关,这样我们就得到前面的条件概率计算简化如下:
这样我们的P(W)计算简化如下:
当k = 0时,这个时候对应的模型叫做一元模型(Unigram model),即wi与它前面的0个词相关,即wi不与任何词相关,每一个词都是相互独立的,P(W)计算如下:
当k = 1时,对应的模型叫做二元模型(Bigram model),此时wi与它前面一个词相关,P(W)计算如下:
同样的,我们可以让k = 2,叫做 trigrams,4-grams,5-grams,当k = N - 1,模型成为n元模型,即N-grams。
总的来说,N-grams有一些不足,因为语言存在一个长距离依赖关系,比如考虑下面的句子:
“The computer which I had just put into the machine room on the fifth floor crashed.”
假如我们要预测最后一个词语crashed出现的概率,如果采用二元模型,那么crashed与floor实际关联可能性应该非常小,相反的,这句子的主语computer与crashed的相关性很大,但是n-grams并没有捕捉到这个信息。
参数估计
要计算出模型中的条件概率,这些条件概率也称为模型的参数,得到这些参数的过程称为训练。用最大似然性估计计算下面的条件概率:
其中c(wi-1)表示wi-1出现的次数,是count的首字母c。对一小段文本看一个例子:
其中<\s>分别表示一个句子的开头和结束,s即start的意思。计算这段文本的二元模型如下:
比如计算P(I | )表示I作为句子开头的概率:
再看一个例子,这个例子来自大一点的语料库,为了计算对应的二元模型的参数,即P(wi | wi-1),我们要先计数即c(wi-1,wi),然后计数c(wi-1),再用除法可得到这些条件概率。可以看到对于c(wi-1,wi)来说,wi-1有语料库词典大小(记作|V|)的可能取值,wi也是,所以c(wi-1,wi)要计算的个数有|V|^2。c(wi-1,wi)计数结果如下:
c(wi-1)的计数结果如下:
那么二元模型的参数计算结果如下:
比如计算其中的P(want | i) = 0.33如下:
那么针对这个语料库的二元模型建立好了后,我们可以计算我们的目标,即一个句子的概率了,一个例子如下:
P( I want english food ) = P(I|) × P(want|I) × P(english|want) × P(food|english) × P(|food) = .000031
我们再看一下该二元模型所捕捉到的一些实际信息:
实际上常常在对数空间里面计算概率,原因有两个:
1.防止溢出,可以看到,如果计算的句子很长,那么最后得到的结果将非常小,甚至会溢出,比如计算得到的概率是0.001,那么假设以10为底取对数的结果就是-3,这样就不会溢出。
2.对数空间里面加法可以代替乘法,因为log(p1p2) = logp1 + logp2,而在计算机内部,显然加法比乘法执行更快!
建立N-GRAM模型这里老师推荐了开源工具包,SRILM( http://www.speech.sri.com/projects/srilm/),以及开源的N-GRAM数据集:http://ngrams.googlelabs.com/
语言模型的评价
我们能够建立语言模型了,一般的我们在训练集上得到语言模型的参数,在测试集里面来测试模型的性能,那么如何去衡量一个语言模型的好坏呢?比较两个模型A,B好坏,一种外在的评价就是将AB放入具体的任务中,然后分别得到模型的准确率,这种方式当然是最好的方式,但这种方式的缺点是过于耗时,在实际情况中往往需要花费过多时间才能得到结果。另一种方式是使用下面要介绍的困惑度,但注意困惑度并不是上述外在评价的一个好的近似,所以一般使用在试点试验上,所谓试点试验就是一个小规模的初步研究,以评估一些性能。
困惑度
困惑度的基本评价方式是对测试集赋予高概率值的模型更好,一个句子W的困惑度(PP)定义如下:
对于二元模型,该公式为:
可以看到,概率越大,困惑度越小,即小的困惑度等于好的模型。且当wi之间是独立的(一元模型),且等概率为p时,公式为:
比如计算一个只包含0~9数字序列的困惑度,每个数字发生的概率是1/10。那么我们得到困惑度PP(W) = 10。这里讲义并没有详细的讲一个测试集上的困惑度是如何定义的,需要一些信息论的概念,有机会再记录学习笔记。
数据稀疏问题
数据稀疏问题,就是由于有限的语料,产生了零概率问题,我们从前面一个例子看:
这个二元模型里面也是相当多的条件概率为0,再比如Shakespeare语料中,作为二元模型 进行训练,结果有99.96%的条件概率为0,我们再看一个例子,在某个训练集中:
… denied the allegations
… denied the reports
… denied the claims
… denied the request
从这个训练集,我们训练得到模型,因为denied the offer在训练集中从没发生过,所以
P(“offer” | denied the) = 0
测试集如下:
… denied the offer
… denied the loan
当我们用这个模型在测试集中测试时,有P(denied the offer) = 0,模型试图说明这个句子不太可能出现,而事实上只是它以前没有见过而已,所以N-GRAM通常只在训练集合和测试集很相似时预测效果才好,而这里出现的零概率问题,也导致不能计算困惑度,因为会导致分母为0。解决N-GRAM的零概率问题是很有必要的,下面讨论一些方法。
平滑方法
平滑方法是用来解决上面语言模型的零概率问题,它的解决问题的基本思想就是把在训练集中看到的概率分一点给未看到的,并保持概率和为1,我们看一个例子图:对某个训练集,计算P(w|denied the)后的统计图:
经过平滑方法后,就变成如下:
下面看一些具体的平滑算法。
Laplace平滑
又称加1平滑,加1 是由于其基本思想是保证所有计数结果至少出现一次,比如为二元模型时,计算公式如下:
这里V是语料词汇量大小,可以想一想为什么分母是加V,因为要保证整个概率和为1,即固定w,对于某个条件概率P(wi | w)要有:
P(w1 | w) + P(w2 | w) + ... = 1
即:
现在在分子上每一个计数都加1了,总共加了V个1,为了保证商为1,分母也要加V。
现在我们用这个平滑法将前面例子重新计数得到如下:
最后得到条件概率结果:
我们最开始讲的平滑算法的都是把看见的概率分给了未看见的概率,我们重新计数一下,我们来对比一下到底分了多少,现在利用平滑后的概率计算新的计数:
利用这个公式,我们看下结果的对比:
所以能够从中看到,对于语言模型,加1平滑并不是一个好的平滑方法,因为它将某些原来的计数大幅削减用于补偿那些未看见的计数。
但它用于一些文本分类还是不错的。
删除插值
删除插值使用线性插值的手段,将高阶模型和低阶模型做线性组合,例如计算三元语法时,把一元语法,二元语法和三元语法结合起来,每种语法用线性权值λ 来加权,公式如下:
还可以把每个λ看成上下文相关的函数,进一步扩展该公式为:(这里没怎么看明白讲义)
为了确定参数λ i,将原始语料中一部分作为留存数据(held-out data),即现在有三个数据集:
用最小化留存数据的困惑度来求的λ i:
1. 求出training data初始模型,并初始化λ i
2.数据集选择留存数据,选择λ i使得下面的概率最大化
Stupid backoff
backoff是退避的意思,回退的含义是比如要计算p(wn | wn-2,wn-1),但没有相关的三元统计,就可以使用二元语法P(wn | wn-2)来估计,如果没有相关的二元统计,那么我们就用一元模型P(wn)来估计。对于一些庞大的语料库,比如Google N-gram语料库,不能直接
拿来用,需要进行剪枝,缩小其规模,如仅使用出现频率大于阈值的n-gram,去掉一些高阶的n-grams等,另外在存储效率上,也可以改变存储的数据结构,改变数据类型等方法。对于这类大规模语料建立的语言模型,所用的平滑方法叫做Stupid backoff:
更好的平滑算法
前面介绍了加1平滑,效果不是很好,更一般的,我们有加k平滑,形式如下:
其中分母V仍然是语料词汇量大小,至于为什么是加kV,可以用前面的推导证实。现在把这个式子转换一下,令
将m带入到加k平滑算法中:
再得到如下公式,与一元模型概率相关(不知道这一步怎么推导过来的)
Unigram Prior平滑效果比较好,但对于语言模型来说仍然不够好。下面依次介绍Good-Turing,Kneser-Ney,Witten-Bell,这几种平滑算法都是用我们只出现一次的计数去估计未看见的。
Good-Turing(古德-图灵)平滑算法
先介绍一个记号Nc = 频数c的频数,举一个例子,对于如下文本:
Sam I am I am Sam I do not eat
分布统计每个单词的出现次数
I 3 sam 2 am 2 do 1 not 1 eat 1
那么可以得到:N1 = 3 N2 = 2 N3 = 1,那么c * Nc =频数为c的词数
了解了这个以后,在举一个例子来说明直观的理解Good-Turing,假设现某人在钓鱼且结果如下:
10 carp, 3 perch, 2 whitefish, 1 trout, 1 salmon, 1 eel = 18 fish
那么下一条鱼是trout的概率是多少? 因为上面trout出现了一次,所以概率是1/18,那如果下一条鱼是新的种类的概率是多少? 因为Good-Turing是将看过一次的计数去估计未看见的,上面N1 = 3,所以概率是3/18,如果用这样的假设的话,只看过一次的概率就要打折分给未看见的,所以前面第一个问题的下一条鱼的概率一定会小于1/18,下面看一下Good-Turing的计算公式:
所以对下一条是未看见的鱼种类的概率:
那么下一条是仅看过一次的鱼种类就如下计算:
可以看到,在最大似然估计下P(trout) = 1/18,现在折扣了2/3,那么对于发生了2次概率呢,比如求下一条鱼是whitefish的概率?c=2时,按照古德-图灵公式c* = 3/2,那么出现两次词语的概率就是3/2/18。所以对于Nk,k重新计数如下:
那么发生了k次词语的概率计算如下:
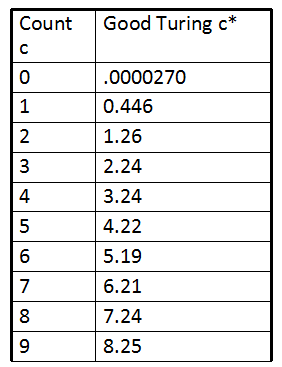
下面对一个样例应用图灵-估计时,计算打折后的数据如下:
一般而言Nk > Nk+1,即发生次数少的单词数多,比如只出现过一次的单词就要比出现两次的单词多,出现两次的单词就要比出现3词的单词多,可以如下图:
那么这种估计存在一个问题,比如按照公式计算发生高频数的词语,c* =(c+1)Nc+1 / Nc,由于c越大,后面就可能不连贯,即Nc+1很可能等于0,所以新的计数结果为0,可以将后面的处理为连续的平滑曲线来做计算,如下:
Kneser-Ney Smoothing
我们再看一下古德-图灵估计的结果:
后面的折扣看上去很固定,大概都是c* = (c - 0.75)左右,即古德-图灵的平滑的折扣是比较固定的,由此引出绝对减值法,下面看绝对减值法的一般公式:
在公式里面我们不直接计算一元模型概率P(w),我们看一个例子:
I can’t see without my reading___________?
下面一个词的是glasses比Francisco更有可能,尽管从一元模型上来说,Francisco出现的概率很高,但它都是跟着San后面出现的,由此,并不直接计算P(w),而是计算 ,表示有多可能w会作为新的延续出现,对每一个词,计算有多少不同的二元统计,即
,表示有多可能w会作为新的延续出现,对每一个词,计算有多少不同的二元统计,即 中有多少个不同的wi-1。
中有多少个不同的wi-1。
分母表示总共有多少个不同的二元统计,用这个公式,就可以看到比较平常的Francisco只能得到较低的概率。所以我们得到Kneser-Ney平滑算法:
其中
更一般的Kneser-Ney递归形式如下:
其中Ckn计算方式如下:
Continuation count就是上面介绍的计算多少个不同的统计,比如二元的wi-1,wi,那么Ckn(wi-1, wi) = |{wi-1: c(wi-1, wi)}|