扫描线算法

背景

之前看到洛谷管理员大佬发明了个二次分块，然后就想学学，发现扫描线是个前置知识，于是来肝这个算法了，好像也不是很难的样子。

进入正题

扫描线一个很经典的例题：在坐标轴上有若干个矩形，问他们覆盖的面积总和。

因为他们覆盖的面积有重复，于是就用到了神奇的扫描线算法。

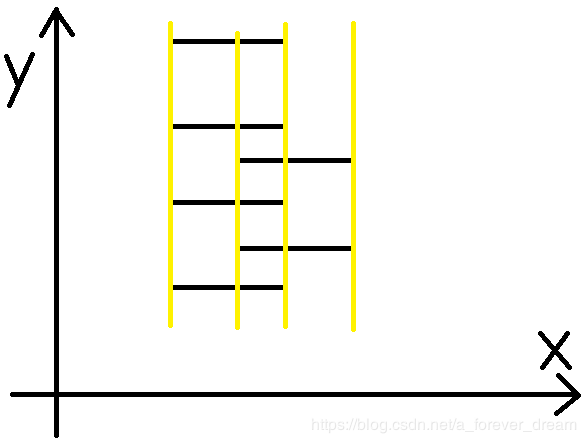
假设有三个矩形，如图：

---

扫描线算法流程：

1. 想象一下有一条平行于 $y$ 轴的直线，正在从左边缓缓向右平移……
2. 再想像一下 $y$ 轴上有一棵线段树，它记录的是 $y$ 轴上每个点的覆盖次数
3. 每当遇到某个矩形的某一条边时，就计算面积——用这次碰边的 $x$ 坐标减去上一次碰边时的 $x$ 坐标，再用这个差值乘以当前 $y$ 轴上有多少个点被覆盖
4. 当这条直线遇到某个矩形的左边时，将这个矩形的左边所对应的y轴区间的覆盖次数 $+1$，当遇到某个矩形的右边时，就相应的 $-1$
5. 让这条线继续向右移动……

（注意，3操作要在4操作之前！）

---

以上面那个为例，演示一下过程。

先给出所有扫描线的位置：

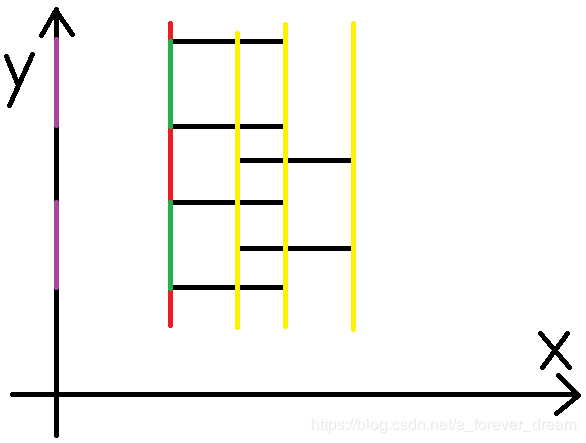
第一条扫描线

绿色的部分便是扫描线与矩形的边重合的部分，y轴上紫色部分就是当前被覆盖的部分，由于这是第一条扫描线，于是不计算面积，直接看下一条。

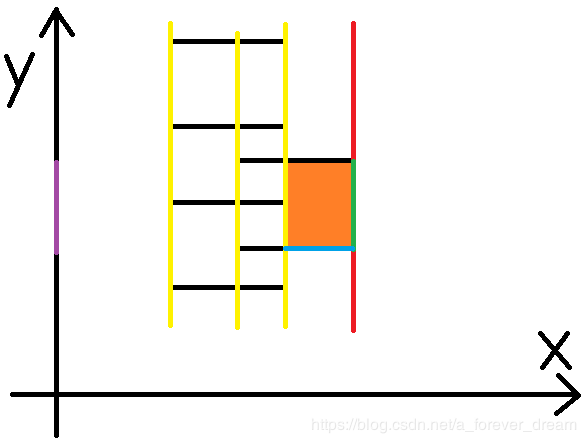
第二条扫描线

1.计算面积
面积就是图中橙色部分，即紫色部分的长度乘蓝色部分的长度。

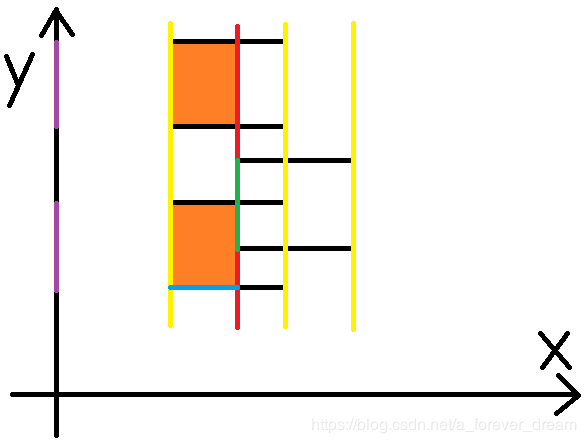
2.更新线段树，即紫色部分
这一次遇到了另一条左边，于是将它在y轴对应的部分的覆盖次数+1。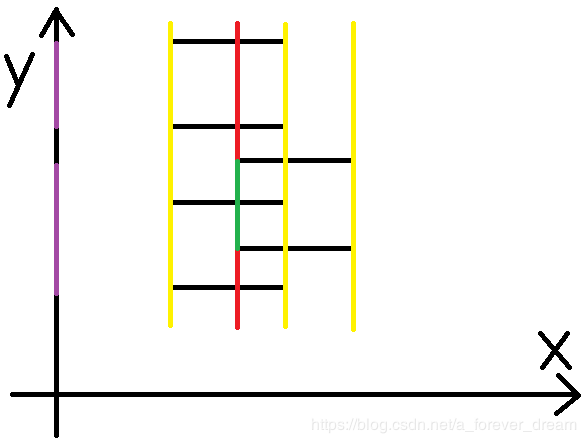

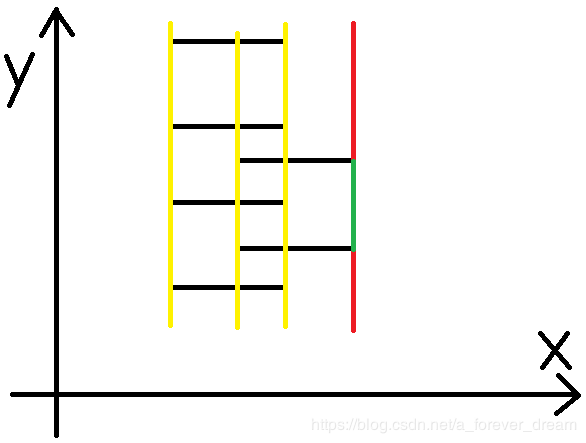
第三条扫描线

1.计算面积
各种颜色的意义如上所述，下面就不解释了。

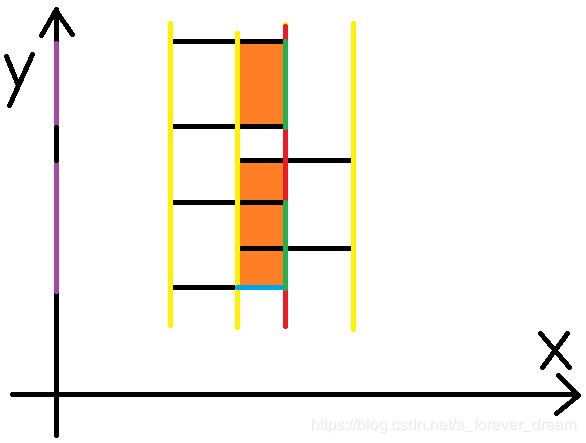
2.更新线段树
由于这次遇到了两条右边，所以线段树对应部分-1。

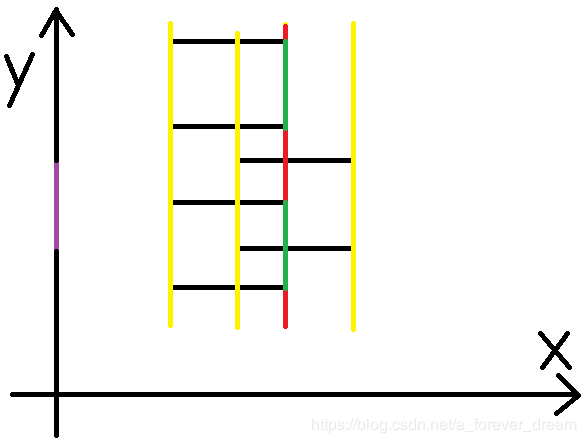
第四条扫描线

1.计算面积

2.更新线段树

以上就是扫描线的流程了。

---

接下来还有最后一个问题，如何计算面积？

两条扫描线的间距是很容易得到的，重点就是线段树部分如何实现。

先把线段树需要执行的操作列出来：

1. 改段（区间 $+1$ or $-1$）
2. 求整个 $y$ 轴上有多少个点的覆盖次数不为0

然后……好像很难做的样子。

但是这道题的操作是有一个特性的——对于每一个 $+1$ 操作，必然有个对应的 $-1$ 操作（两个操作区间相同），也就是说，这两个操作所修改的线段树上的节点是完全相同的。

利用这个性质，就可以轻松实现了，具体实现方式见如下代码：

struct node{
    int l,r,z,cover;//z记录有多少个不为0的点
    //cover记录自己管理的区间的被整体覆盖次数，而不是管理区间内每个点的被覆盖次数的总和
    node *zuo,*you;
    node():zuo(NULL),you(NULL),z(0),cover(0){}
    void buildtree(int x,int y)//建树
    {
    	l=x,r=y;
        if(x<y)
        {
            int mid=x+y>>1;
            zuo=new node;zuo->buildtree(x,mid);
            you=new node;you->buildtree(mid+1,y);
        }
    }
    void change(int x,int y,int c)
    {
        if(l==x&&r==y)
        {
            cover+=c;
            if(cover==0)z=zuo!=NULL?zuo->z+you->z:0;//如果覆盖次数为0，那么就取左右儿子的z的和
            if(cover==1)z=r-l+1;
            return;
        }
        if(y<=zuo->r)zuo->change(x,y,c);
        else if(x>=you->l)you->change(x,y,c);
        else zuo->change(x,zuo->r,c),you->change(you->l,y,c);
        if(cover==0)z=zuo->z+you->z;
    }
};

这只是扫描线的一个应用，并不是所有题都是扫矩形的，也会有扫点的题目。

总而言之，扫描线的中心思想就是：将要处理的内容排序，然后按顺序处理。所以使用扫描线有个很显然的前提：支持离线计算答案。

---

例题——Atlantis

题目传送门

题目大意：与上面的例题基本相同，只是每个点的坐标是浮点数。

如果坐标不是整数的话，y轴上的每个点就不能表示出来了。但是矩形数量是有限的，也就是说用到的y轴上的点是有限的，我们只需要把这些用到的记下来，排个序，用他们来建线段树即可。但是要注意，这次的线段树的叶子结点记录的不是y轴上的点，而是两点之间的那段空隙。也就是像下面这样：

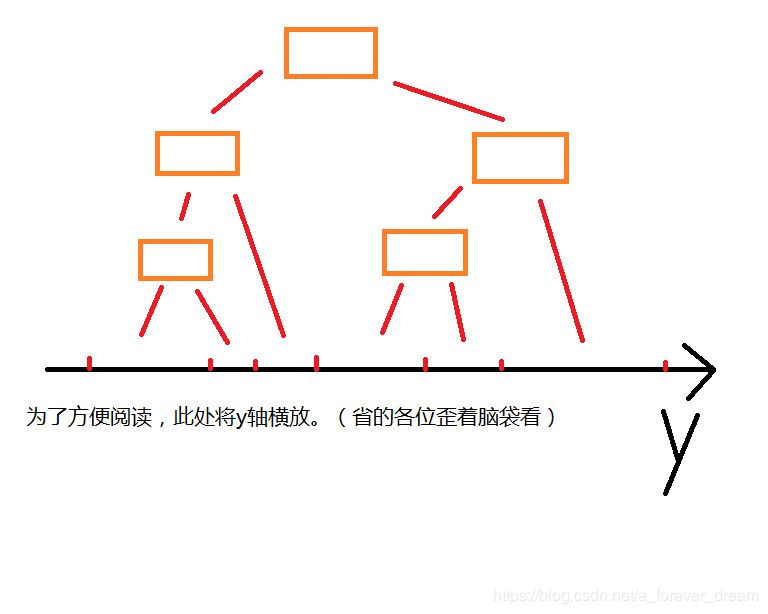
关于其他细节的话，就看代码吧，这里先给出线段树部分的代码（变化不大）：

double l,r,z;
    int cover;
    node *zuo,*you;
    node():zuo(NULL),you(NULL),z(0),cover(0){}
    void buildtree(int x,int y)
    {
        l=yy[x],r=yy[y];//yy是 所有用到的y轴的点 排好序之后的集合
        if(y-x>1)//注意这里，由于叶子结点记录的是两点中间的那一段，所以假如x~y之间有两段及以上时才继续分给儿子
        {
            int mid=x+y>>1;
            zuo=new node;zuo->buildtree(x,mid);
            you=new node;you->buildtree(mid,y);
        }
    }
    void change(double x,double y,int c)
    {
        if(l==x&&r==y)
        {
            cover+=c;
            if(cover==0)z=zuo!=NULL?zuo->z+you->z:0;
            if(cover>=1)z=r-l;//注意这里不用+1，与上面相比，因为是浮点数计算
            return;
        }
        if(y<=zuo->r)zuo->change(x,y,c);
        else if(x>=you->l)you->change(x,y,c);
        else zuo->change(x,zuo->r,c),you->change(you->l,y,c);
        if(cover==0)z=zuo->z+you->z;
    }
    void del()//因为题目有多组数据，所以每次用完一棵线段树之后就顺手删掉，当然没有这个也能AC
    {
        if(zuo!=NULL)zuo->del(),you->del();
        delete this;
    }

完整代码（由于以前的代码又臭又长，于是忍不住在 2020.6.14 更新了一个新的代码）：

#include 
#include 
using namespace std;
#define db double
#define maxn 1010

int T,n,t=0,tt; db Y[maxn];
struct edge{db x,y1,y2;int type;}a[maxn];
bool cmp(edge x,edge y){return x.x<y.x;}
struct node{
	db l,r,z;int cover;node *zuo,*you;
	node(int x,int y):l(Y[x]),r(Y[y]),cover(0),z(0){
		if(y-x>1)zuo=new node(x,x+y>>1),you=new node(x+y>>1,y);
		else zuo=you=NULL;
	}
	void pushup(){
		if(cover)z=r-l;else if(!zuo)z=0;
		else z=zuo->z+you->z;
	}
	void change(db x,db y,int z)
	{
		if(l==x&&r==y){cover+=z;pushup();return;}
		if(y<=zuo->r)zuo->change(x,y,z);
		else if(x>=you->l)you->change(x,y,z);
		else zuo->change(x,zuo->r,z),you->change(you->l,y,z);
		pushup();
	}
}*root;

int main()
{
	while(scanf("%d",&n),n!=0)
	{
		T++;t=0;for(int i=1;i<=n;i++)
		{
			db x,y,xx,yy;
			scanf("%lf %lf %lf %lf",&x,&y,&xx,&yy);
			a[++t]=(edge){x,y,yy,1}; Y[t]=y;
			a[++t]=(edge){xx,y,yy,-1}; Y[t]=yy;
		}
		sort(a+1,a+t+1,cmp);sort(Y+1,Y+t+1);
		tt=unique(Y+1,Y+t+1)-(Y+1);root=new node(1,tt);
		db ans=0;for(int i=1;i<=t;i++){
			ans+=(a[i].x-a[i-1].x)*root->z;
			root->change(a[i].y1,a[i].y2,a[i].type);
		}
		printf("Test case #%d\nTotal explored area: %.2lf\n\n",T,ans);
	}
}

更多好题

窗口的星星       题解