算法学习之路：盛最多水的容器

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

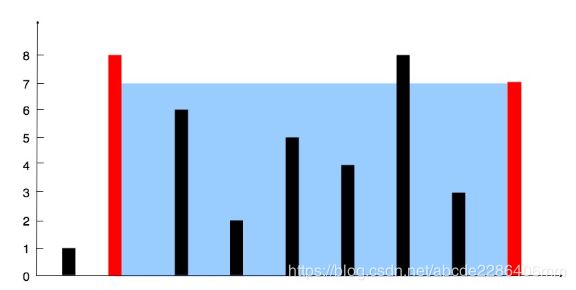
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

 

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/container-with-most-water

 

本题有两个做法，最简单粗暴的方法也就是双循环直接遍历所有容器体积，本次不对该方法进行探究，探究另一个方法：双指针。

顾名思义，双指针就是头尾两个指针分别向中间聚拢以求得最大面积，这里面会出现一些问题：

1.双指针如何移动，何时移动？

2.为何能保证移动之后不会丢失最大值？

我们利用(head,ahead)(tail,atail)表示组成容器的两个坐标点，那么容器的长度length = tail-head，宽度 wide = min(ahead,atail)，面积s = min(ahead,atail) * (tail-head)，设置初始值为第一个坐标和最后一个坐标，那么我们已知，无论如何移动head或者tail,都会使得长度-1，假设我们移动的是宽度最长的坐标，那么由于容器的面积始终取决于最短的宽度，得到的面积会始终小于原始的面积（宽度变小，长度变小），因此，反过来想，假设总是移动最短的一根，那么得到的面积有可能会比原来的大（宽度变大，长度变小），但是这样一来，相较于暴力破解法的双循环，我们便直接排除了以min(wide)为宽的所有情况（该情况面积始终更小），因此，每次都移动短边可以有效的避免无意义的容器计算且保证最大值不会被过滤（永远只会过滤面积更小的情况）。

上代码：

package com.ucarinc.wtf.demo;
/**
 * @ProjectName: shiro-demo
 * @ClassName: MaxArea
 * @Author: [email protected]
 * @Description:
 * @Date: 2020/5/13 11:11
 * @Version: 1.0
 */
public class MaxArea {
    public static int maxArea(int[] height) {
        int maxArea = 0;
        int i = 0;
        int j = height.length - 1;
        for (; i < j;){
            maxArea = Math.max(Math.min(height[i] , height[j]) * (j - i),maxArea);
            if (height[i] < height[j]){
                i ++;
            }else {
                j--;
            }
        }
        return maxArea;
    }
}