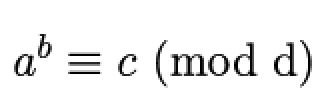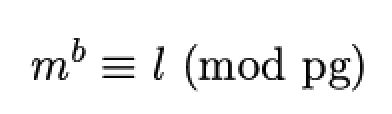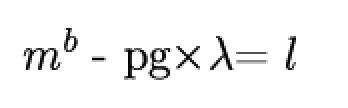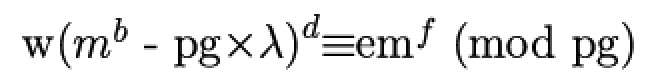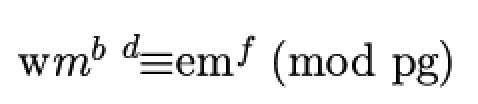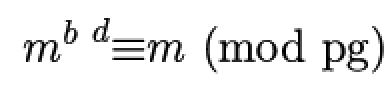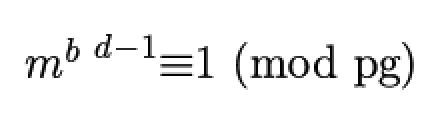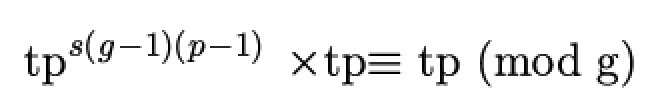1.找出不可破的密码系统(1)
这是家鼎鼎有名的赌场——皇家赌场。没错,你就是James Bond
由于刚刚和歹徒的斗智斗勇,现在你已精疲力竭。但你依然故作轻松,和女神谈笑风生,实际上两腿发软,楼梯都走不牢。女神的兴致很高,空气中弥漫着迷人的女性荷尔蒙的芬芳。
为了不让女神发现自己是个大虚B,你决定发送密文向助手求助,让他假装服务生送点蓝色小药丸进来。
因为你知道女神绝非等闲之辈,她是智慧与美貌的化身。同时天天与犯罪分子周旋的她做事极其小心。这不——在你打开电脑的同时,她已经在路由上抓包了。
魔高一尺,道高一丈。在这之前,你和助手已经精心准备,构建了一套完善的密码系统。而这套密码系统是不可破解的。
长期和坏人作斗争的你非常明白人类的智慧是无穷尽的,再精心构造的编码也会有更聪明的人破译出来。加上你平时猥琐、自负的性格,你脑中冒出一个想法——你要设计一套并不是由精妙编码得到的密文,也就是说直接能开放解决方式却得不到结果的加密方法。
进一步想下去,这个方法只能通过暴力来破解,他的计算量会是天文数字。用自然数的思想来说,就是你知道下一步是什么,应该怎么做,却永远也得不到终点。
你越想越兴奋。
我们展开这个思路,接着走。这个思路要求自己的同伙给到自己一套数字,而你利用这套数字对内容进行加密。同伙给你的这套数字是经过一系列计算而得到的几个数字之一,而其他部分他要保留不传送给你,因为这个部分是用来解密的。
也就是说,解开密文的钥匙生成了加密的另一把钥匙,加密的钥匙也可以倒推出解密的钥匙,而且干脆摆出来让你推倒。光是这么一想,你便猥琐地笑了。
江湖上流传的将只是一把能上锁却解不了锁的钥匙。
2.找出不可破的密码系统(2)
解决问题的思路实际上就是一个分解因子的过程,那么不可解的钥匙,可以理解为这是一串不可分解的数字,然而他实际上是有因子的。也就是说在待加密内容所需要的公钥是由几个因子计算组合出来的。生成这个组合的方式又却简单的不行,以方便解密。
组合因子最简单的方式是什么呢?
没错,就是乘法,两个因子的乘法。(自然不会是加减法、也不会是除法,关于这一点大家可以自己想出来)
看来,我们已经有思路去设计这套密码系统了。
可以互相约分就不叫因子了,因此我们现在要找的就是,生成两个质数的办法。然后这个质数要足够大,算得死所有的计算机。
这是真的吗?
当问题开始见到曙光的时候,我们必须不能被兴奋冲昏头脑,要重新回顾一下我们的初衷。我们现在基本上确定了质因数分解这个思路,那么这个问题足够困难吗?
我们可以试想一下,如果一个超大数由两个质数相乘得到,我们要对其分解,首先自然是猜测一个可能值,然后向上向下分别判定出素数,最后相乘比对。
如果有看过3825123056546412979是一个素数? - 这一篇,我们会了解到首先大数的素数判定就很存在问题,一方面我们的精度范围实际上不够大(380亿亿还不够大吗?实际上,确实不够);另一方面,随着数的变大,我们可以保证两个质因子之差大得惊人,一个个试错的成本不可估量。
那么我们有没有必要对这两个质因子进行更复杂的操作?比如引入多个质因子,进行更复杂的变换得到公钥?
但是我们要考虑总体的计算成本和经济效益,我们的加密解密成本要无限低于破解成本。当我们能实现不可破之后,再去做点什么就像在正无穷后面加上一串,可以是可以,但是没有必要。
初步看来,我们的构想是有可行性的,那么不管最终结果怎样,我们先得试一把,没准大法就蹦出来了。
我们设质因子是p和g,m是密文,l是加密后内容,ak是公钥,sk是私钥,f是生产密钥的过程,F是加密过程,G是解密过程,则我们可以构造密码系统的雏形:
首先我们分析f过程,我们知道破解这个系统的关键在于找到p和g的值,那么f过程意味着必须使用他们,并且对他们进行了变换处理。而这个处理的结果要能以用来解开由他们之乘积进行进一步运算形成密文。
看来f过程不能胡乱写啊。思路似乎被掐断了,但不要放弃,想一想被女神知道自己是个大虚B的严重后果,我们还是硬着头皮继续吧。或者,想一想女人的汗津津的胴体,再大的苦也得吃啊!
我有说过解决一个问题的过程是从混沌中分解因子的过程。既然他是一个问题就肯定是一个判定,就会有条件和结果。(这种思路在分解一个描述性语句上会出错,比如一个内部各语句无限循环嵌套的系统。这个系统的复杂度是如此之高,互相调用,自指,导致定义本身的沦为形式。上来就用一判定命题的方式来指责它是容易的,然而它本身不存在被证明的需要。我说的是哪个系统呢?如果有时间,我会尝试去描述它。)
我们现在来分解这个密码系统的流程。先从抽象程度较高的F(即加密)过程开始。因为太过于接近具体算法,意味着更难立马想出。
F有两个参数m和ak,通过这两个参数我们得到了密文l。
当我们有两个参数时,我们能做些什么?
首先排除加法和减法,因为这还不如直接发明文呢。然后是其他诸如乘法、冥运算、除法,看似没有什么问题。但是我们要知道,我们的目标是ak直接暴露啊。如果仅通过这样的运算,看来是远远不够的。
我们需要至少引入一个新数,这个数帮助我们增加了密文l的复杂度。而且这个新数引进之后所带来的计算最好还能引进一些不确定性。
这是因为当一个拥有4个参数的等式,3个为已知量时,我们肯定能找到剩下的未知量。为了增加找到的难度,我们要设法让数字尽量的膨胀,另外要找到把4个参数变成更多参数的办法。
第一种思路很好解决,引入冥运算。导致解出原文的最后一步必须是开n次方。对于这样的难度我颇为满意.
第二个思路便比较难办,如何制造一个新参数?是什么样的运算在计算时仅需要三个参数,但逆运算需要四个参数?按常理,这所谓的第四个参数应该蕴含在结果之中,为什么无故消失了?它为什么可以约去而不影响等式的成立?
是的,没错。加密是一个求余过程,密文中所不能体现的正是商数。但我们要逆推出原文,必须得把这个商数找到,如果这个商足够大,重试次数也跟着上升到近乎无限。
现在我们可以先把加密算法写下来:
其中最容易确定的是a肯定是原文,这是由于我们要让最后一步逆运算为开n次方。另外考虑到加密的经济性,b最好避免使用两大质数的乘积,而且应该是一个不是很大数字。我们初步先这样确定,看看接下来会发生什么。根据这样的安排,那么d就是p和g这两个大质数的积了。b则是引入的新数。这个数肯定将会由接收方(即解密方)提供,否则将导致解密方也无法看到原文。
因此这个b的出现应该是在生产sk的过程,即f过程中产生。
3.找出不可破的密码系统(3)
我们现在来看一下生成sk的过程。为了让破解这套系统不可避免的经历分解质因数的过程,我们知道,sk中的求解过程必定不能包含直接使用两质数之积,因为这样就没有必要去破解质因数了。
同时为了保证算法简单,我们只需对两个质数经行简单的变换即可。最小的变化量,即向上向下取1 。但是我们这个行为还得先打住,因为我们随意的变换可能导致密文不可解。
我们先来尝试求解一下原文m,根据:
刚才说到,我们的加密算法会导致解密过程中不可避免的需要开n(在这里是b)次方。但这真的不可避免吗?
倘若这是不可避免的,那么这意味着这套密码系统的暴力破解方式和正常解密过程是同一个——这是非常不合理的设计。
那么,这是不是意味着我们要推倒重来,重新设计这套密码系统?
如果真的是这样,那真的让人很丧气,上锁的部分已经让这套密码系统初露峥嵘,其威力已经可以预见。虽然说,前期投入很多并不意味着一个方案就是不可放弃的。
但是,放弃的前提是做出了足够多的尝试。
让我再回到公开的数字b上,让我们先回答一个问题,我们是如何创造出b的?
我们发现在加密过程中仅有两个参数不足以产生有强度的密文,那么同样的,很容易发现解密过程中仅仅传入密文和sk这两个参数是不足以解开密文的。两个参数运算规则太简单。
看来,我们至少要再构造出一个新数字。
在明确这个数字出现在哪?是什么?之前,我们必须先构造出解密的大致方法。可以确定的是密文l存在向后得到m的潜能,那么至少l中包含m这个元素,但通过解密运算,与m无关的参数又会被约去,根据之前的加密规则,我们可知:
也就是说,等式左边不包含m的成分将会被很自然的约去,(也就是这一部分为0)而不影响两边保持相等。这会是什么样的运算呢?
看来解密过程也是模运算,模pg求余数,而这个余数就是我们的原文m。或关于m与一些已知量的运算。我们先把现在得到解密运算表达出来:
因为求模pg的值,那么包含pg的项我们都可以约去,于是以上和下面的式子等价:
单看这个式子我们似乎进入了无法求解的状态。因为解开它要求知道的量实在太多。看来是我们构造的式子太过一般化,而且就算是已知这些量,求解起来的计算量也不小。比如f的值如果偏大,开f次方会是个不小的工程,而我们知道密码系统强有力的原因并不在此,不相关的计算,何况是这样如此增加能耗的计算,我们应该去避免。
根据这样的思想,我们先把上式简化,我们可以试试看最终有没有途径得到它:
如果bd=1,上式显然成立,但也就不存在任何加密意义。d必须是由p和g经过变换生成,而d应该是这个过程中的副作用。但这个想法为我们提供了宝贵的思路,将上式两边除以m,得:
有没有熟悉的感觉呢?在费马和欧拉一篇中,我们构造的欧拉定理就是这个形式,如果m与pg互质,表明bd-1=sφ(pg)。
现在我们还需要考察的是否b、d有解,否则还是白搭。因为p、g是已知量且为质数,所以φ(pg)=(p-1)(g-1) 。带入可知,该方程是一个丢番图方程的形式。我们只须保证b与φ(pg)互质,该方程便有解。即可解出我们的密钥d。
我们已经找到了b、d生成的方法,而且这种方法满足我们必须首先知道两个质数的值的约定。但是似乎只在原文m与pg互质的情况下才生效,那么这一定代表这种生成方法在其他情况下注定失效吗?
我们不妨来检验一下。
假设我们如有神助,原文m正好是tpg,那么怎么解都是0,也算是符合这个办法。
假设我们半神相助,原文m=tp或m=tg,
我们又该如何构造出上面的式子呢?
因为bd-1=sφ(pg)=s(p-1)(g-1),因此我们要在指数部分构造出p-1和g-1,这个好办,还是根据欧拉定理,我们先从m=tp入手,毕竟这两种情况一种能行得通,另外一种也肯定可以。我们可知:
既然等于1了,我们在指数部分多乘一些东西根本不会产生影响,那么我们边将ed的其他部分扔进去,可得:
也就是:
现在我们需要把p给构造进入模中。看上去不太可能。不过,光凭看上去做事情,人类应该还在林子里摘野果子吃。
我们只需把这个式子展开,得到:
两边同乘以tp,这样就把p元素带入了,可得:
是的。不可破的密码系统我们已经建设完了!
在女神面前保持刚强形象还真是不容易啊!
4. RSA的核心
如果对RSA算法有过一点了解,大家会发现通过上面的过程,我们自己构造出了RSA。如果早生个几十年,RSA说不定就叫西门算法之类的了。
关于这套密码系统,我们不得不提一下蒙哥马利算法
网上一般这样介绍蒙哥马利算法:
是RSA算法的核心之一
这句话非常具有意义,就如同你花100块大洋买了本《人脑全解》,结果这是一本由白纸装订的书,就封皮上有一句话:
大脑是人的核心组件之一。没脑子的人会死。
除了精屁,实在找不出别的形容词。
其实加几个字,效果就完全不同了:
蒙哥马利算法是RSA加密解密过程中提高性能的核心办法
关于这个算法,大家可以去看3825123056546412979是一个素数? -
在这篇文章中,我们将会构造出蒙哥马利算法。
除了这个算法之外,要我说RSA的核心,我觉得应该是:
充分相信但凡是人类设计的密码系统肯定能被人类破译
无论设计多大的弯路,都会被走穿
那么我们干脆设计一条笔直的没有尽头的路吧!