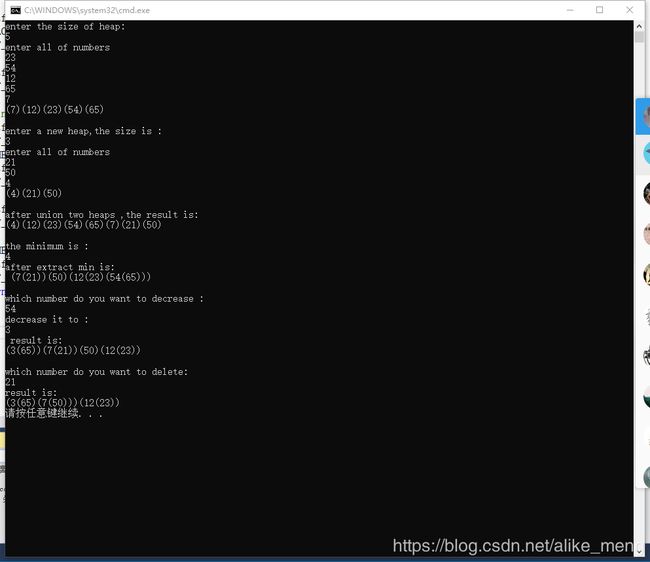
斐波那契堆

基本上是按照算法导论写的。
结果还是运行不出来，然后参照了这个博主（非常推荐这个博主，写了很多算法导论的博客用C写的）：
https://www.cnblogs.com/skywang12345/p/3659060.html

说下要注意的地方吧，看完书之后纯敲代码都搞了接近两天才弄出来，还是看了别人的写的，哭晕了都…
从上到下：
struct _heap的结构我开始是没有用maxDegree的，感觉写了也没啥用，主要就是在后面算最大度的时候要弄一个数组，数组的上界就是这个堆的最大的度，那个数组我是通过书上介绍的用数学方法算的最大度Dn

*说到类型不匹配，我看了好多博主的代码总是在某个函数的参数就用到指针了，H这样的，我感觉自己还是没太搞明白为什么要这样，我的代码了基本都没有这样用，除了那种交换两个结点，不用指针根本就交换不了。

FIB_CONNECT这个函数看他的实现似乎有点复杂，但是把两个双向链表画出来，指针跟着动一动就能看出来了，这里就不上传过程了。我开始就是这里弄麻烦了，参照了别的博主的简便方法。

在创建结点和堆的时候要把该初始化的全都初始化了，不然会在后面测试的时候碰见很多野指针，就直接给你按任意键继续活着走不动了。一断点跟踪就能发现0xcdcdcdcd了。

UNION这个函数书上是创建了一个新的堆，然后再去操作的，我也这样写了，错了，然后换了上面那个博主的方法，就地给他UNION了。

双向链表用起来感觉还是有那么一点不习惯，判断是不是已经循环了一圈的时候用到do while这个语句，我以前都没有用过这个，在这里体现到他的便利了。

extract_min写起来真的相当麻烦，里面又用到了几个其他的函数，然后错了也不好调，慢慢写吧慢慢改吧。

注意对结点的操作就是对结点为根的树的操作，他们是通过parent，child指针维系起来的。然后就涉及到怎么处理他的孩子，还要考虑到孩子又那么多个又是双向链表怎么操作。

search和print一如既往的递归，还是一个完整括号一棵小树的方法去看

还有就是斐波那契堆只是最小堆的集合，并没要求怎么去合并，只是有合并的函数可以写出来，所以开始输出的结果都是没有只做了插入，没有任何处理的结果，从最小的结点开始向右输出的结果。后面extract—min之后就用到consolidate了就有了合并的结果了，看了一下应该没有问题

// 斐波那契堆.cpp: 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include
#include
#include
#include //要使用memset是要包含此头文件
#include
#define MAX  1000000

typedef  struct _FNode *FIBNode;
typedef struct _FNode
{
	int key;
	FIBNode child;
	FIBNode parent;
	FIBNode left;
	FIBNode right;
	int degree;
	bool mark;
}Node;


typedef struct  _Heap *FIBHeap;
typedef struct _Heap
{
	FIBNode min;
	int number;             //根链表的元素个数
	int maxDegree;
}Heap;

void EXCHANGE_NODE(FIBNode *x, FIBNode *y)                //交换两个结点
{
	FIBNode t;
	t = *x;
	*x = *y;
	*y = t;
}
void EXCHANGE_HEAP(FIBHeap *H1, FIBHeap *H2)          //交换两个堆
{
	FIBHeap *t=NULL;
	*t = *H1;
	*H1 = *H2;
	*H2 = *t;
}
//把b接到a的后面
void FIB_CONNECT(FIBNode a, FIBNode b)              //把图画出来就明白了   
{
	FIBNode temp;
	temp = a->right;
	a->right = b->right;
	b->right->left = a;
	b->right = temp;
	temp->left = b;
}

FIBNode MAKE_FIB_NODE(int k)            //创建一个关键字为k的结点
{
	FIBNode x = NULL;
	x = (FIBNode)malloc(sizeof(Node));
//	memset(x, 0, sizeof(FIBNode));             //这一行很重要，之前都运行不出来，指针会出错，给他先置0就好了，如果没有置为k的话
	x->left = x->right = x;
	x->key = k;
	x->degree = 0;
	x->child = x->parent = NULL;             /////////////////不要出现野指针！！！！！下面用到child的时候就野了！！！！！
	return x;
}
FIBHeap MAKE_FIB_HEAP()
{
	FIBHeap H = NULL;
	H = (FIBHeap)malloc(sizeof(Heap));
//	memset(H, 0, sizeof(FIBHeap));
	H->number = 0;
	H->min = NULL;
	H->maxDegree = 0;
	return H;
}

//结点x插入结点y之前
void FIBNode_Add(FIBNode x, FIBNode y)             ///////
{
	x->left = y->left;
	x->right = y;
	y->left->right = x;
	y->left = x;
}
//将结点移除来
void REMOVE_NODE_FROM_HEAP(FIBHeap H, FIBNode z)          ////////////
{
	z->left->right = z->right;
	z->right->left = z->left;
//	z->left = z->right = NULL;
	
//	H->number = H->number - 1;
}
void FIB_HEAP_INSERT(FIBHeap H,FIBNode x)
{

	if (H->min == NULL)             //是一个空堆
	{
		//create a root list for H containing just x
		H->min = x;
		H->number = 1;
	}
	else
	{
		//insert x into H's root list
		FIBNode_Add(x,H->min);
		if (x->key < H->min->key)
			H->min = x;
		H->number = H->number + 1;
	}
}
FIBHeap FIB_HEAP_UNION(FIBHeap H1, FIBHeap H2)            
{
	//就地组合，没有新建一个heap
//	FIBNode temp;
	if (H1 == NULL)
		return H2;
	else if (H2 == NULL)
		return H1;
	///////////////以下操作实现H2添加到H1中
	if (H2->maxDegree > H1->maxDegree)
		EXCHANGE_HEAP(&H1, &H2);
	if ((H1->min) == NULL)        //H1没有最小结点
	{
		H1->min = H2->min;
		H1->number = H2->number;
		free(H2);      //用完free
	}
	else if ((H2->min) == NULL)       //H1有最小结点，H2没有
	{
		free(H2);
	}
	else             //两个都有最小结点
	{
		FIB_CONNECT(H1->min, H2->min);
		if (H1->min->key > H2->min->key)
			H1->min = H2->min;
		H1->number = H1->number + H2->number;
		free(H2);
	}
	return H1;

}

//将最小的结点从根链表里面移除。最小结点包括他组成的树一并移除
FIBNode FIB_REMOVE_MIN(FIBHeap H)       
{
	FIBNode min = H->min;
	if (H->min == min->right)     //只有一个结点
	     H->min = NULL;
	else
	{
		REMOVE_NODE_FROM_HEAP(H,min);
		H->min = min->right;
	}
	min->left = min->right = min;          //把原来的最小结点独立出来
	return min;
}

void FIB_HEAP_LINK(FIBHeap H, FIBNode y, FIBNode x)                  //y变成x的孩子
{
	REMOVE_NODE_FROM_HEAP(H,y);
	if (x->child == NULL)
		x->child = y;
	else
		FIBNode_Add(y, x->child);

	y->parent = x;
	x->degree++;
	x->mark = false;
}

void CONSOLIDATE(FIBHeap H)
{
	int  d, Dn;
	FIBNode x, y;
	H->maxDegree = (int)((double(log(H->number*1.0))) / (double(log(2.0))) + 1);
	Dn = H->maxDegree;
	FIBNode *A;       //指向指针的数组。 //let A[0...to D(H.n)] be a new array                
	//记录根节点的度数  A[i]=y  即  y->degree=i  D(H.n)是整个堆中所有根节点中度数最大的结点的度数   要动态才能搞出这个数组
	A = (FIBNode*)malloc(sizeof(FIBNode)*Dn);
	for (int i = 0; i <= Dn; i++)
	{
		A[i] = NULL;                         //指针数组内全是空
	}
	while (H->min != NULL)
	{
		x = FIB_REMOVE_MIN(H);      //去除最小的树
		d = x->degree;    //最小树的度
		while (A[d] != NULL)
		{
			y = A[d];
			if (x->key > y->key)
				EXCHANGE_NODE(&x, &y);       //两个结点的指针，结点是对应一棵树的
			FIB_HEAP_LINK(H, y, x);
			A[d] = NULL;
			d++;
		
		}
		A[d] = x;

	}
	H->min = NULL;
	//将A[d]中的结点添加到根表中去，A[d]中的结点是唯一度的
	for (int i = 0; i < Dn; i++)
	{
		if (A[i] != NULL)
		{
			if (H->min == NULL)    //最先不为空的度（也就是最小的非空度）为min   
			{
				H->min = A[i];
			}
			else
			{
				FIBNode_Add(A[i], H->min);
				if (A[i]->key < H->min->key)
					H->min = A[i];
			}
		}
	}

}


FIBNode FIB_HEAP_EXTRACT_MIN(FIBHeap H)
{
	if (H == NULL || H->min == NULL)
		return NULL;
	FIBNode child=NULL;
	FIBNode min = H->min;
	while (min->child != NULL)
	{
		child = min->child;
		REMOVE_NODE_FROM_HEAP(H, child);    //先把孩子移除来再加根链表
		if (child->right == child)
			min->child = NULL;
		else
			min->child = child->right;

		FIBNode_Add(child, H->min);      //把最小结点的孩子结点都放在根链表里面去
		child->parent = NULL;
	}
	REMOVE_NODE_FROM_HEAP (H,min);       //把最结点拿出来，在维护最小结点的性质
	if (min->right == min)
		H->min = NULL;
	else
	{
		H->min = min->right;
		CONSOLIDATE(H);

	}
	H->number--;
	return min;
}
void EXTRACT_MIN(FIBHeap H)
{
	FIBNode z=NULL;
	if (H == NULL || H->min == NULL)
		return;
	z = FIB_HEAP_EXTRACT_MIN(H);
	if (z != NULL)
		free(z);
}

void CUT(FIBHeap H, FIBNode x, FIBNode y)  //y is parent ,x is child
{
	//remove x from the child list of y,decreamenting y.degree
	REMOVE_NODE_FROM_HEAP(H, x);
	y->degree--;
	if (x->right == x)       //y只有一个孩子
		y->child = NULL;
	else
		y->child = x->right;

	x->parent = NULL;
	x->left = x->right = x;
	x->mark = false;
	FIBNode_Add(x, H->min);
}

void CASCADING_CUT(FIBHeap H, FIBNode y)
{
	FIBNode z = y->parent;
	if (z != NULL)
		return ;
	
	if (y->mark == false)
		y->mark = true;
	else
		{
			CUT(H, y, z);
			CASCADING_CUT(H, z);
		}
	
}

///////////search 有问题
FIBNode _SEARCH_NODE(FIBNode node, int k)            //递归查找结点,node is H->min
{
	FIBNode t = node;
	FIBNode p = NULL;
	if (node== NULL)
	{
		return node;
	}
	do
	{
		if (t->key == k)
		{
			p = t;
			break;
		}
		else
		{
			if ((p = _SEARCH_NODE(t->child, k)) != NULL)
				break;
		}
		t = t->right;               //////////////////记得走指针啊
	} while (t != node);

	return p;

}
FIBNode SEARCH_NODE(FIBHeap H, int k)
{
	if (H == NULL || H->min == NULL)
		return NULL;

	return _SEARCH_NODE(H->min, k);
}

void FIB_HEAP_DECREASE_KEY(FIBHeap H, FIBNode x, int k)
{
	if (H == NULL || H->min == NULL || x == NULL)
		return;
	if (k >= x->key)
		//error new key is greater than current key
		return ;
	x->key = k;
	FIBNode y = x->parent;
	if (y != NULL && x->key < y->key)
	{
		CUT(H, x, y);
		CASCADING_CUT(H, y);

	}
	if (x->key < H->min->key)
	{
		H->min = x;
	}
}

void FIB_HEAP_DELETE(FIBHeap H, FIBNode x)
{
	FIB_HEAP_DECREASE_KEY(H, x, -MAX);
	FIB_HEAP_EXTRACT_MIN(H);
}

void PRINT(FIBNode x)              
{
	FIBNode p = NULL;
	if (x == NULL)
		return;
	p = x;
	do
	{
		printf("(");
		printf("%d", p->key);
	
		if (p->child!=NULL )
		{
			PRINT(p->child);
		}
		printf(")");
		p = p->right;
	} while (p != x);

}
void PRINT_(FIBHeap H)
{
	PRINT(H->min);
	printf("\n");
}

int main()                  //delete decrease 应该没有问题  extract 可能没有问题
{
	int size1, size2, k1, k2;
	FIBHeap heap = MAKE_FIB_HEAP();
	FIBHeap new_heap = MAKE_FIB_HEAP();
	FIBHeap H = MAKE_FIB_HEAP();
	FIBNode  node1, node2;

	printf("enter the size of heap:\n");
	scanf_s("%d", &size1);
	printf("enter all of numbers\n");
	for (int i = 0; i < size1; i++)           //构建第一个斐波那契堆
	{
		scanf_s("%d", &k1);
		node1 = MAKE_FIB_NODE(k1);
	//	node1->key = k1;
		FIB_HEAP_INSERT(heap,node1);
	}
	PRINT_(heap);

	printf("\nenter a new heap,the size is :\n");           //构建第二个斐波那契堆
	scanf_s("%d", &size2);
	printf("enter all of numbers\n");
	for (int i = 0; i < size2; i++)
	{
		scanf_s("%d", &k2);
		node2 = MAKE_FIB_NODE(k2);
	//	node2->key = k2;
		FIB_HEAP_INSERT(new_heap,node2);
	}
	PRINT_(new_heap);
	
	//system("pause");
	
	printf("\nafter union two heaps ,the result is:\n");       //检验合并
	H=FIB_HEAP_UNION(heap,new_heap);
	PRINT_(H);

	printf("\nthe minimum is :\n");
	printf("%d", H->min->key);

	printf("\nafter extract min is:\n ");   //检验extract min
	EXTRACT_MIN(H);
	PRINT_(H);

	printf("\nwhich number do you want to decrease :\n");   //检验decrease  
	scanf_s("%d", &k1);
	node1 = SEARCH_NODE(H, k1);
	//printf("这是search到的%d", node1->key);
	printf("decrease it to :\n");
	scanf_s("%d", &k2);
	FIB_HEAP_DECREASE_KEY(H, node1, k2);
	printf(" result is:\n");
	PRINT_(H);

	printf("\nwhich number do you want to delete:\n");
	scanf_s("%d", &k1);
	node1 = SEARCH_NODE(H, k1);
	FIB_HEAP_DELETE(H, node1);
	printf("result is:\n");
	PRINT_(H);
	return 0;
}