周志华老师西瓜书读书笔记——第一章:绪论
文章目录
- 1. 基本术语
- 2. 假设空间
- 3. 归纳偏好
- 4. 机器学习发展过程中几大思想
- 5. 机器学习&数据挖掘
- 6.习题
- Q&A
1. 基本术语
| 中文 | English |
|---|---|
| 数据集 | data set |
| 样本 | sample |
| 属性空间 | attribute space |
| 样本空间 | sample space |
| 训练集 | training set |
| 标记 | label |
| 回归 | regression |
| 正类 | positive class |
| 反类 | negative class |
| 聚类 | clustering |
| 监督学习 | supervised learning |
| 泛化 | generalization |
监督学习:分类和回归,训练数据有标记信息
无监督学习:聚类,训练数据没有标记信息
泛化能力:指训练得到的模型适用于新的样本
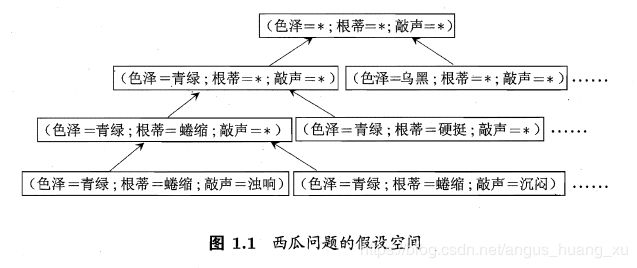
2. 假设空间
有点类似决策树
3. 归纳偏好
同样的训练集可能训练出不同的模型,它们在面对新的样本时输出不一样,这是由于算法的“偏好”不同导致的。
一个机器学习算法的好坏很大程度上受“归纳偏好”影响。"奥卡姆剃刀"是一种帮助建立"正确"偏好的原则。
奥卡姆剃刀(Occam’s razor):若有多个假设与观察一致,选最简单的那个
对于二分类问题且所有的二值函数f按均匀分布对误差求和:
∑ f E o t e ( L a ∣ X , f ) = ∑ f ∑ h ∑ x ∈ X − X P ( x ) I ( h ( x ) ≠ f ( x ) ) P ( h ∣ X , L a ) = ∑ x ∈ X − X P ( x ) ∑ h P ( h ∣ X , L a ) ∑ f I ( h ( x ) ≠ f ( x ) ) = ∑ x ∈ X − X P ( x ) ∑ h P ( h ∣ X , L a ) 1 2 2 ∣ χ ∣ = 1 2 2 ∣ X ∣ ∑ x ∈ X − X P ( x ) ∑ h P ( h ∣ X , L a ) \begin{aligned} \sum_{f} E_{o t e}\left(\mathfrak{L}_{a} | X, f\right) &=\sum_{f} \sum_{h} \sum_{x \in \mathcal{X}-X} P(\boldsymbol{x}) \mathbb{I}(h(\boldsymbol{x}) \neq f(\boldsymbol{x})) P\left(h | X, \mathfrak{L}_{a}\right) \\ &=\sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \sum_{h} P\left(h | X, \mathfrak{L}_{a}\right) \sum_{f} \mathbb{I}(h(\boldsymbol{x}) \neq f(\boldsymbol{x})) \\ &=\sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \sum_{h} P\left(h | X, \mathfrak{L}_{a}\right) \frac{1}{2} 2^{|\chi|} \\ &=\frac{1}{2} 2^{|\mathcal{X}|} \sum_{x \in \mathcal{X}-X} P(\boldsymbol{x}) \sum_{h} P\left(h | X, \mathfrak{L}_{a}\right) \end{aligned} f∑Eote(La∣X,f)=f∑h∑x∈X−X∑P(x)I(h(x)̸=f(x))P(h∣X,La)=x∈X−X∑P(x)h∑P(h∣X,La)f∑I(h(x)̸=f(x))=x∈X−X∑P(x)h∑P(h∣X,La)212∣χ∣=212∣X∣x∈X−X∑P(x)h∑P(h∣X,La)
二值函数f共有 2 ∣ X ∣ 2^{|\mathcal{X}|} 2∣X∣个,故 ∑ f I ( h ( x ) ≠ f ( x ) ) = 1 2 2 ∣ X ∣ \sum_{f}\mathbb{I}(h(x)\neq f(x))=\frac 12 2^{|\mathcal{X}|} ∑fI(h(x)̸=f(x))=212∣X∣
结果与 L a \mathfrak{L}_{a} La无关!!!与学习算法无关!!!
没有免费的午餐定理(NFL定理):学习算法的误差与学习算法的聪明程度无关!
前提是:所有问题出现的概率相同
4. 机器学习发展过程中几大思想
-
符号学习主义:决策树,基于逻辑的学习
基于逻辑的学习如:归纳逻辑程序设计(ILP):一阶谓词逻辑
PS:数理逻辑有涉及
-
从样例中学习:
早期是死记硬背式学习,信息的存储与检索
后期发展成为神经网络
著名的BP算法:实际上是一个反馈机制,大致过程如下:
- 将训练集输入,得到输出;
- 将输出结果与实际结果比较,算出误差;
- 误差由输出端传入,反向传播分摊个各层各个单元;
- 根据分摊的误差修正个单元的权值,使误差取极小值
- 重复此过程
-
统计学习?
我感觉神经网络应该也能算一种统计学习
大规模的数据训练出来的算法?
5. 机器学习&数据挖掘
数据挖掘=数据管理+数据分析
数据管理 ⟶ \longrightarrow ⟶数据库技术
数据分析 ⟶ \longrightarrow ⟶机器学习和统计学
6.习题
1.1 画出树状图较为简单
1.2 共有 4* 3 * 3 +1 = 37种假设
1.3 噪声产生在哪个属性上就对该属性“相信”少一点,即分配的权值少一点
1.4
∑ f E o t e ( L a ∣ X , f ) = ∑ f ∑ h ∑ x ∈ X − X P ( x ) ℓ ( h ( x ) , f ( x ) ) P ( h ∣ X , L a ) = ∑ f ∑ x ∈ X − X P ( x ) ℓ ( h ( x ) , f ( x ) ) \sum_{f}E_{o t e}\left(\mathfrak{L}_{a} | X, f\right)=\sum_{f}\sum_{h} \sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \ell(h(\boldsymbol{x}), f(\boldsymbol{x})) P\left(h | X, \mathfrak{L}_{a}\right)\\ =\sum_{f}\sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \ell(h(\boldsymbol{x}), f(\boldsymbol{x}))\\ f∑Eote(La∣X,f)=f∑h∑x∈X−X∑P(x)ℓ(h(x),f(x))P(h∣X,La)=f∑x∈X−X∑P(x)ℓ(h(x),f(x))
结果与 L a \mathfrak{L}_{a} La无关
Q&A
-
训练集,测试集,验证集各自的英文名是哪些?为什么要划分为这几个数据集?划分比例一般是多少?
training set; testing set; validation set;
划分的目的自然是为了训练出来的模型误差更小。
使用训练集进行训练,验证集进行评估和误差计算并根据误差做出调整;最后使用测试集测试调整出的模型。举一反三,反复测试方能使模型取得更好的效果。
划分比例一般是:训练集50%;测试集和验证集都是25%
-
“监督学习”和“无监督学习”的区别在哪里?是否所有学习方式可以归为这两种学习方式中的一种?
区别在于训练数据有没有标记信息。
监督学习是人为的给数据打上标记,比如标明好瓜和坏瓜;
而非监督学习是让机器做到将相似的样本分为一类,不人为提供标记作为标准。
监督学习有训练集,测试集,验证集,模型是通过测试集和验证集训练出来的;
非监督只提供一组数据,让机器从中找规律分类
半监督学习:大量未标记数据和少量标记数据
强化学习:一种"试错"的学习方法,每次给出对机器行为的评价信号,让其自我修正。
-
“泛化”是什么意思?它和过拟合之间的关系是什么?
泛:宽,广泛。泛化就是指用有限的数据得到的模型适用于更宽一点的数据,即模型适用于新的样本。
过拟合粗俗的理解就是:训练的模型完全为训练样本服务,和训练样本更贴近,但是和整个样本的分布相差反而大一点。
过拟合表示模型的泛化能力变弱,不适用于新的样本
-
“奥卡姆剃刀”原则是什么?它和“泛化”之间有什么关联吗?
奥卡姆剃刀原则简单的理解为最简单原则,如果多个假设与观察一致,选择最简单的
从自然规律的角度看:奥卡姆剃刀原则一般能选出泛化能力更强的模型;
但是不排除有些刁钻的样本使得与简单的模型相差甚远,导致模型泛化能力减弱。