PyTorch基础
目录
一、PyTorch中的Tensor张量
1、Tensor张量
2、Tensor数据类型
3、Tensor常用函数
二、基于PyTorch搭建简易神经网络模型
1、简易神经网络模型
2、Pytorch自动梯度
3、使用自动梯度和自定义函数搭建简易神经网络模型
三、torch.nn和torch.optim
1、使用torch.nn搭建神经网络模型
2、使用torch.optim优化模型
一、PyTorch中的Tensor张量
1、Tensor张量
Tensor在PyTorch中负责存储基本数据,PyTorch针对Tensor也提供了相对丰富的函数和方法,所以PyTorch中的Tensor与NumPy的数组具有极高的相似性,同时 Tensor可以使用 GPU 进行计算。
2、Tensor数据类型
(1)torch.FloatTensor # 此变量用于生成数据类型为浮点型的Tensor,传递给torch.FloatTensor的参数可以是一个列表,也可以是一个维度值;
import torch
a=torch.FloatTensor(2,3) #生成数据类型为浮点型的Tensor
print(a)
b=torch.FloatTensor([2,3,4,5])
print(b)tensor([[0., 0., 0.],
[0., 0., 0.]])
tensor([2., 3., 4., 5.])(2)torch.IntTensor # 用于生成数据类型为整型的Tensor
3、Tensor常用函数
(1)torch.rand # 用于生成数据类型为浮点型且维度指定的随机Tensor,和在Numpy中使用numpy.rand生成随机数的方法类似,随机生成的浮点数据在0~1区间均匀分布。
(2)torch.randn # 用于生成数据类型为浮点型且维度指定的随机Tensor,和在Numpy中使用numpy.randn生成随机数的方法类似,随机生成的浮点数的取值满足均值为0,方差为1的正太分布。
(3)torch.range # 用于生成数据类型为浮点型且自定义其实范围和结束范围的Tensor,所以传递给torch.range的参数有三个,分别是范围的起始值,范围的结束值和步长,其中,步长用于指定从起始值到结束值的每步的数据间隔。
(4)torch.zeros # 用于生成数据类型为浮点型且维度指定的Tensor,不过这个浮点型的Tensor中的元素值全部为0。
(5)torch.abs # 将参数传递到torch.abs后返回输入参数的绝对值作为输出,输出参数必须是一个Tensor数据类型的变量。
(6)torch.add # 将参数传递到torch.add后返回输入参数的求和结果作为输出,输入参数既可以全部是Tensor数据类型的变量,也可以是一个Tensor数据类型的变量,另一个是标量。
(7)torch.clamp # 对输入参数按照自定义的范围进行裁剪,最后将参数裁剪的结果作为输出。所以输入参数一共有三个,分别是需要进行裁剪的Tensor数据类型的变量、裁剪的上边界和裁剪的下边界,具体的裁剪过程是:使用变量中的每个元素分别和裁剪的上边界及裁剪的下边界的值进行比较,如果元素的值小于裁剪的下边界的值,该元素就被重写成裁剪的下边界的值;同理,如果元素的值大于裁剪的上边界的值,该元素就被重写成裁剪的上边界的值。
a=torch.randn(2,3)
print(a)
b=torch.clamp(a,-0.1,0.1) #边界值裁剪
print(b)tensor([[-0.6895, -0.2334, -1.1246],
[ 0.2961, -1.4742, 1.7083]])
tensor([[-0.1000, -0.1000, -0.1000],
[ 0.1000, -0.1000, 0.1000]])(8)torch.div # 将参数传递到torch.div后返回输入参数的求商结果作为输出,同样,参与运算的参数可以全部是Tensor数据类型的变量,也可以是Tensor数据类型的变量和标量的组合。
(9)torch.pow # 将参数传递到torch.pow后返回输入参数的求幂结果作为输出,参与运算的参数可以全部是Tensor数据类型的变量,也可以是Tensor数据类型的变量和标量的组合。
(10)torch.mul # 将参数传递到 torch.mul后返回输入参数求积的结果作为输出,参与运算的参数可以全部是Tensor数据类型的变量,也可以是Tensor数据类型的变量和标量的组合。
(11)torch.mm # 将参数传递到 torch.mm后返回输入参数的求积结果作为输出,不过这个求积的方式和之前的torch.mul运算方式不太样,torch.mm运用矩阵之间的乘法规则进行计算,所以被传入的参数会被当作矩阵进行处理,参数的维度自然也要满足矩阵乘法的前提条件,即前一个矩阵的行数必须和后一个矩阵的列数相等,否则不能进行计算。
(12)torch.mv # 将参数传递到torch.mv后返回输入参数的求积结果作为输出,torch.mv运用矩阵与向量之间的乘法规则进行计算,被传入的参数中的第1个参数代表矩阵,第2个参数代表向量,顺序不能颠倒。
(13)torch.view # 改变一个 tensor 的大小或者形状。
x=torch.randn(4,4)
y=x.view(16)
z=x.view(-1,8) #-1表示该维度大小是从其他维度推断出来的
print(x.size(),y.size(),z.size())torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8])二、基于PyTorch搭建简易神经网络模型
1、简易神经网络模型
# coding:utf-8
import torch
batch_n = 100 #一个批次中输入数据的数量,值是100表示在一个批次中输入100个数据
input_data = 1000 #每个数据包含的数据特征
hidden_layer = 100 #经过隐藏层后保留的数据特征的个数
output_data = 10 #输出数据表示分类结果值的数量
#初始化权重
x = torch.randn(batch_n, input_data) #输入层维度为(100,1000)
y = torch.randn(batch_n, output_data) #输出层维度为(100,10)
w1 = torch.randn(input_data, hidden_layer) #输入层到隐藏层的权重参数维度为(1000,100)
w2 = torch.randn(hidden_layer, output_data) #隐藏层到输出层的权重参数维度为(100,10)
epoch_n = 20 #训练的次数
learning_rate = 1e-6 #学习效率
#梯度下降优化神经网络参数
for epoch in range(epoch_n):
h1 = x.mm(w1) # 100*1000
h1 = h1.clamp(min=0) #使用clamp方法进行裁剪,将小于零的值全部重新赋值于0
y_pred = h1.mm(w2) # 100*10
# print(y_pred)
loss = (y_pred - y).pow(2).sum() #均方误差计算损失
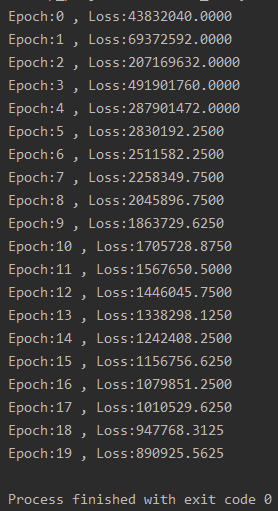
print("Epoch:{} , Loss:{:.4f}".format(epoch, loss))
gray_y_pred = 2 * (y_pred - y)
gray_w2 = h1.t().mm(gray_y_pred) #.t()是将Tensor进行转置
grad_h = gray_y_pred.clone()
grad_h = grad_h.mm(w2.t())
grad_h.clamp_(min=0)
grad_w1 = x.t().mm(grad_h) #权重参数对应的梯度
w1 -= learning_rate * grad_w1 #根据学习率对w1和w2的权重参数进行更新
w2 -= learning_rate * gray_w2结果如下:
2、Pytorch自动梯度
autograd package 是PyTorch中所有神经网络的核心,它提供了Tensors上所有运算的自动求导功能,通过torch.autograd包,可以使模型参数自动计算在优化过程中需要用到的梯度值,在很大程度上帮助降低了实现后向传播代码的复杂度。
torch.autograd 包的主要功能是完成神经网络后向传播中的链式求导。
autograd.Variable 是这个package的中心类。它打包了一个Tensor,并且支持几乎所有运算。一旦你完成了你的计算,可以调用.backward(),所有梯度就可以自动计算。
3、使用自动梯度和自定义函数搭建简易神经网络模型
import torch
from torch.autograd import Variable
#构建神经网络模型
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
#super().__init__()
def forward(self,input,w1,w2):
x=torch.mm(input,w1)
x=torch.clamp(x,min=0)
x=torch.mm(x,w2)
return x
def backward(self):
pass
batch_n = 100 # 批量输入的数据量
hidden_layer = 100 # 通过隐藏层后输出的特征数
input_data = 1000 # 输入数据的特征个数
output_data = 10 # 最后输出的分类结果数
#初始化权重
x = Variable(torch.randn(batch_n, input_data), requires_grad=False)
y = Variable(torch.randn(batch_n, output_data), requires_grad=False)
w1 = Variable(torch.randn(input_data, hidden_layer), requires_grad=True)
w2 = Variable(torch.randn(hidden_layer, output_data), requires_grad=True)
epoch_n = 20 #训练的次数
learning_rate = 1e-6 #学习效率
model=Model() #对模型类进行调用
#模型训练和参数优化
for epoch in range(epoch_n):
y_pred = model(x,w1,w2) #完成对模型预测值的输出
loss = (y_pred - y).pow(2).sum()
print("Epoch:{} , Loss:{:.4f}".format(epoch, loss.data))
loss.backward() #自动计算所有梯度
w1.data -= learning_rate * w1.grad.data
w2.data -= learning_rate * w2.grad.data
w1.grad.data.zero_()
w2.grad.data.zero_()结果如下:
代码说明:
(1)class Model(torch.nn.Module)
首先通过class Model(torch.nn.Module)完成了类继承的操作,之后分别是类的初始化,以及forward函数和backward函数。forward函数实现了模型的前向传播中的矩阵运算,backward实现了模型的后向传播中的自动梯度计算,后向传播如果没有特别的需求,则在一般情况下不用进行调整。
(2)requires_grad参数
这个参数的赋值类型是布尔型,如果requires_grad的值是False,那么表示该变量在进行自动梯度计算的过程中不会保留梯度值。我们将输入的数据x和输出的数据y的requires_grad参数均设置为False,这是因为这两个变量并不是我们的模型需要优化的参数,而两个权重w1和w2的requires_grad参数的值为True。
(3).backward()函数
这个函数的功能在于让模型根据计算图自动计算每个节点的梯度值并根据需求进行保留,有了这一步,我们的权重参数 w1.data和 w2.data就可以直接使用在自动梯度过程中求得的梯度值w1.data.grad和w2.data.grad,并结合学习速率来对现有的参数进行更新、优化了。
(4).zero_()函数
将本次计算得到的各个参数节点的梯度值通过grad.data.zero_()全部置零,如果不置零,则计算的梯度值会被一直累加,这样就会影响到后续的计算。
三、torch.nn和torch.optim
torch.nn 包提供了很多与实现神经网络中的具体功能相关的类,这些类涵盖了深度神经网络模型在搭建和参数优化过程中的常用内容,比如神经网络中的卷积层、池化层、全连接层这类层次构造的方法、防止过拟合的参数归一化方法、Dropout 方法,还有激活函数部分的线性激活函数、非线性激活函数相关的方法等。
torch.optim 包中提供了非常多的可实现参数自动优化的类,比如SGD、AdaGrad、RMSProp、Adam等。
1、使用torch.nn搭建神经网络模型
# _*_coding:utf-8_*_
import torch
from torch.autograd import Variable
batch_n = 100 # 批量输入的数据量
input_data = 1000 # 输入数据的特征个数
hidden_layer = 100 # 通过隐藏层后输出的特征数
output_data = 10 # 最后输出的分类结果数
x = Variable(torch.randn(batch_n, input_data), requires_grad=False)
y = Variable(torch.randn(batch_n, output_data), requires_grad=False)
# 模型搭建
models = torch.nn.Sequential(
# 首先通过其完成从输入层到隐藏层的线性变换
torch.nn.Linear(input_data, hidden_layer),
# 经过激活函数
torch.nn.ReLU(),
# 最后完成从隐藏层到输出层的线性变换
torch.nn.Linear(hidden_layer, output_data)
)
epoch_n = 10000
learning_rate = 1e-4
loss_fn = torch.nn.MSELoss() #均方误差损失函数
# 迭代优化
for epoch in range(epoch_n):
y_pred = models(x)
loss = loss_fn(y_pred, y)
if epoch % 1000 == 0:
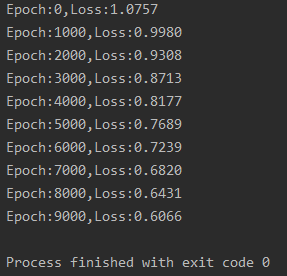
print("Epoch:{},Loss:{:.4f}".format(epoch, loss.data))
models.zero_grad()
loss.backward()
# 访问模型中的全部参数是通过对“models.parameters()”进行遍历完成的
# 对每个遍历的参数进行梯度更新
for param in models.parameters():
param.data -= param.grad.data * learning_rate结果如下:
代码说明:
(1)torch.nn.Sequential
torch.nn.Sequential 类是torch.nn中的一种序列容器,通过在容器中嵌套各种实现神经网络中具体功能相关的类,来完成对神经网络模型的搭建,最主要的是,参数会按照我们定义好的序列自动传递下去。我们可以将嵌套在容器中的各个部分看作各种不同的模块,这些模块可以自由组合。
模块的加入一般有两种方式,一种是在以上代码中使用的直接嵌套,另一种是以 orderdict 有序字典的方式进行传入,这两种方式的唯一区别是,使用后者搭建的模型的每个模块都有我们自定义的名字,而前者默认使用从零开始的数字序列作为每个模块的名字。两种方式如下:
import torch
from torch.autograd import Variable
batch_n = 100 # 批量输入的数据量
input_data = 1000 # 输入数据的特征个数
hidden_layer = 100 # 通过隐藏层后输出的特征数
output_data = 10 # 最后输出的分类结果数
#模型搭建
models = torch.nn.Sequential(
# 首先通过其完成从输入层到隐藏层的线性变换
torch.nn.Linear(input_data, hidden_layer),
# 经过激活函数
torch.nn.ReLU(),
# 最后完成从隐藏层到输出层的线性变换
torch.nn.Linear(hidden_layer, output_data))
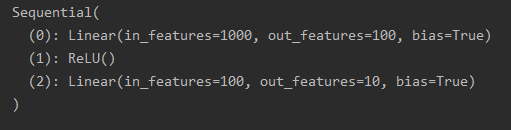
print(models)结果如下:
import torch
from torch.autograd import Variable
from collections import OrderedDict
batch_n = 100 # 批量输入的数据量
input_data = 1000 # 输入数据的特征个数
hidden_layer = 100 # 通过隐藏层后输出的特征数
output_data = 10 # 最后输出的分类结果数
#模型搭建
models = torch.nn.Sequential(OrderedDict([
("Linel",torch.nn.Linear(input_data,hidden_layer)),
("ReLU1",torch.nn.ReLU()),
("Line2",torch.nn.Linear(hidden_layer,output_data))]))
print(models)结果如下:
(2)torch.nn.ReLU
torch.nn.ReLU 类属于非线性激活分类,在定义时默认不需要传入参数。在 torch.nn包中还有许多非线性激活函数类可供选择,比如PReLU、LeakyReLU、Tanh、Sigmoid、Softmax等。
(3)torch.nn.Linear
torch.nn.Linear 类用于定义模型的线性层,即完成前面提到的不同的层之间的线性变换。它接收的参数有三个,分别是输入特征数、输出特征数和是否使用偏置,设置是否使用偏置的参数是一个布尔值,默认为True,即使用偏置。
在实际使用的过程中,我们只需将输入的特征数和输出的特征数传递给torch.nn.Linear类,就会自动生成对应维度的权重参数和偏置,对于生成的权重参数和偏置,我们的模型默认使用了一种比之前的简单随机方式更好的参数初始化方法。
(4)torch.nn.MSELoss
torch.nn.MSELoss 类使用均方误差函数对损失值进行计算,在定义类的对象时不用传入任何参数,但在使用实例时需要输入两个维度一样的参数方可进行计算。
import torch
from torch.autograd import Variable
loss_f=torch.nn.MSELoss()
x=Variable(torch.randn(100,100))
y=Variable(torch.randn(100,100))
loss=loss_f(x,y)
print(loss)tensor(2.0491)其它损失函数使用方法同torch.nn.MSELoss是一样的,如:torch.nn.L1Loss 类使用平均绝对误差函数对损失值进行计算;torch.nn.CrossEntropyLoss 类用于计算交叉熵;
2、使用torch.optim优化模型
# _*_coding:utf-8_*_
import torch
from torch.autograd import Variable
batch_n = 100 # 批量输入的数据量
input_data = 1000 # 输入数据的特征个数
hidden_layer = 100 # 通过隐藏层后输出的特征数
output_data = 10 # 最后输出的分类结果数
x = Variable(torch.randn(batch_n, input_data), requires_grad=False)
y = Variable(torch.randn(batch_n, output_data), requires_grad=False)
# 模型搭建
models = torch.nn.Sequential(
# 首先通过其完成从输入层到隐藏层的线性变换
torch.nn.Linear(input_data, hidden_layer),
# 经过激活函数
torch.nn.ReLU(),
# 最后完成从隐藏层到输出层的线性变换
torch.nn.Linear(hidden_layer, output_data)
)
epoch_n = 20
learning_rate = 1e-4
loss_fn = torch.nn.MSELoss() # 均方误差损失函数
optimzer=torch.optim.Adam(models.parameters(),lr=learning_rate) #
# 训练模型
for epoch in range(epoch_n):
y_pred = models(x)
loss = loss_fn(y_pred, y)
print("Epoch:{},Loss:{:.4f}".format(epoch, loss.data))
optimzer.zero_grad() # 参数梯度的归零
loss.backward()
optimzer.step() # 进行梯度更新结果如下:
代码说明:
(1)torch.optim.Adam
这里使用了 torch.optim 包中的 torch.optim.Adam 类作为我们的模型参数的优化函数,在 torch.optim.Adam 类中输入的是被优化的参数和学习速率的初始值,如果没有输入学习速率的初始值,那么默认使用0.001这个值。因为我们需要优化的是模型中的全部参数,所以传递给torch.optim.Adam类的参数是models.parameters。另外,Adam优化函数还有一个强大的功能,就是可以对梯度更新使用到的学习速率进行自适应调节。
(2)optimzer.zero_grad 和 optimzer.step
optimzer.zero_grad 完成对模型参数梯度的归零。
optimzer.step 主要功能是使用计算得到的梯度值对各个节点的参数进行梯度更新。
参看:
1. PyTorch安装:PyTorch官网
2. Pytorch官方教程中文版