数字图像处理的python实践(11)——傅里叶变换和快速傅里叶变换
前面接触了空间域图像增强,现在要来学习频率域的图像增强。
对于一维的连续函数,定义域为整个时间轴的非周期函数f(t),它的傅里叶变换为
对应的逆傅里叶变换为
一维的离散函数 (其中x=0,1,2,...,M-1) 的傅里叶变换和逆变换为
对于二维的情况,二维连续函数f(x,y)的傅里叶变换为
在数字图像处理中我们关心的自然是,二维离散函数的傅里叶变换,直接给出二维离散傅里叶变换(Discrete Fourier Transform, DFT)的公式:
其中u=0,1,2,...,M-1,V=0,1,2,...N-1。
下面来定义傅里叶变换的幅度谱、相位谱和功率谱。
幅度谱
![]()
显然,幅度谱关于原点具有对称性。![]() 。
。
相位谱
通过幅度谱和相位谱,可以还原F(u,v)。因为相位描述的就是角度的关系,与正切直接相关。
![]()
功率谱(谱密度)
![]()
幅度谱又叫频率谱,是图像增强钟关心的主要对象。频域下每一点的幅值都表示该频率的正弦平面波在叠加中所占的比例。相位谱则是隐含了实部Re和虚部Im之前的比例关系,因此和图像结构息息相关。但是在实际使用时,DFT的直接实现效率较低,所以有人提出了快速傅里叶变换(Fast Fourier Transform,FFT),提高了计算的速度。了解到这个地方,实际上还是很难像空间域那样子直观地体会到作用,只能硬着头皮继续看后续的一些研究,把基础的知识都了解到了然于心才能够好好往后学。
对于一维的离散函数f(x),或者说一个N点序列,它的DTF变换和逆变换为
其中![]() 。我们可以看到,计算每个u对应的F(u)需要执行N次乘法运算和N-1CI1复数加法,因此为了计算长度为N的序列的傅里叶变换,一共需要执行N*N次乘法和N(N-1)次复数加法。看得出计算量巨大,因为其中有许多的重复计算。首先f(x)是我们离散函数的序列值,是变化的,没办法从中改进。但是
。我们可以看到,计算每个u对应的F(u)需要执行N次乘法运算和N-1CI1复数加法,因此为了计算长度为N的序列的傅里叶变换,一共需要执行N*N次乘法和N(N-1)次复数加法。看得出计算量巨大,因为其中有许多的重复计算。首先f(x)是我们离散函数的序列值,是变化的,没办法从中改进。但是![]() 是一个复变量,当序列的长度为N时也一共有N个值,并且不是完全独立的,也有一定的对称性。
是一个复变量,当序列的长度为N时也一共有N个值,并且不是完全独立的,也有一定的对称性。
首先,我们知道![]() 。那么有
。那么有
![]()
进而可以推导出W矩阵元素具有一定的周期性和对称性。
![]()
利用W的周期性,DTF运算中的某些项就可以合并;利用W的对称性,则可以仅计算半个W序列。
按时间抽取的基-2FFT算法
按时间抽取的FFT算法,是基于将输入序列f(x)分解(抽取)成较短序列,然后从这些序列的DFT中求得输入序列F(u)的方法。由于抽取后的较短序列仍然可分,所以最终仅需要计算一个很短序列的DFT。在这种算法中,我们首要关注的就是序列长度为2的整数次幂的序列,这种DFT运算称之为基-2DFF。
设序列长度为![]() ,所以我们可以根据奇偶把输入序列f(x)分成两组,用
,所以我们可以根据奇偶把输入序列f(x)分成两组,用![]() 表示序号为偶数的元素组成的序列,用
表示序号为偶数的元素组成的序列,用![]() 表示序号为奇数的元素组成的序列。
表示序号为奇数的元素组成的序列。
则f(x)的傅里叶变换F(u)可以表示为f(x)的奇数项和偶数项分别组成的序列,变换形式为
其中r=0,1,2,...,N/2-1。因为![]() ,所以上式可以继续化简为
,所以上式可以继续化简为
容易发现,上式中的第一项为f(2r)的N/2点DFT,第二项求和部分是f(2r+1)的N/2点DFT。N/2点DFT是什么意思?它表示的是,我们首先指导f(2r)这个序列的长度正是N/2,所以在前面我们也知道这个下标对应的也是长度,所以这个求和,就恰好是f(2r)这个序列的DFT,长度为N/2。所以第二项也就是f(2r+1)这个长度为N/2的序列的DFT。
![]()
我们用![]() 和
和![]() 分别表示f(2r)和f(2r+1)的N/2点DFT。另外根据DFT序列的周期性特点,还可以得到如下的式子
分别表示f(2r)和f(2r+1)的N/2点DFT。另外根据DFT序列的周期性特点,还可以得到如下的式子
此处的N/2也可以代表周期。
并且,![]() ,我们还可以得出
,我们还可以得出
![]()
因此,
所以有以下两条式子
![]()
以上这是一个递推公式。其中的含义是,一个偶数长度的序列的傅里叶变换,可以通过它的奇数项和偶数项的傅里叶变换得到,从而可以将输入序列分成两部分分别计算之后按照公式相加/相减,在这个过程中,只需要计算![]() ,u=0,1,2,...,N/2-1。因为我们讨论的是基-2的FFT算法,所以N/2会一直是偶数直到为1。是偶数即意味着还可以继续分割,可以持续到每个序列只需要2点的DFT。
,u=0,1,2,...,N/2-1。因为我们讨论的是基-2的FFT算法,所以N/2会一直是偶数直到为1。是偶数即意味着还可以继续分割,可以持续到每个序列只需要2点的DFT。
举个简单的例子,现在输入序列f(x)的长度是8。那么我们按序号来分成奇数项1,3,5,7和偶数0,2,4,6,然后计算各自的DFT。对于1,3,5,7这个四个数组成的序列的DFT,可以把3和7归入奇数项,1、5归入偶数项,再去分别计算DFT;对于0,2,4,6组成的序列的DFT,可以由0,4组成的奇数项的DTF,以及偶数项2,6组成序列的DFT来计算得到。然后取3,7为例,3是相当于偶数项,7是奇数项,已经无法在分割了,此时才开始根据定义来分别计算DFT。这就是基-2FFT的思路。
其实思路不是很复杂,都是代码我居然弄了两天,一直算出来的结果和用np.fft.fft计算出来的不一样。后来慢慢排查,才发现是用来作为临时变量的数组,会跟着原数组改变,总之是拷贝的问题,用了copy.copy之后结果就没问题了。代码如下,运行后可以看到结果相同。其中的函数 Dec2Bin_Inverse2Dec,功能是将01234567这样子排序的数组,根据输出时的新的顺序去调换成04261537,具体为什么要这样做有疑问的可以查找一下其他的资料中的蝶形算法示意图,就可以看清楚了。
import numpy as np
import math
import copy
def dft1(src, dst = None):
'''
One dimension discrete fourier transform.
'''
l = len(src)
result = np.zeros((l), dtype = "complex")
for i in range(l):
for j in range(l):
result[i] += src[j]*np.exp(complex(0,-2*np.pi*i*j/l))
return result
def fft1(src, dst = None):
'''
src: list is better.One dimension.
'''
l = len(src)
n = int(math.log(l,2))
bfsize = np.zeros((l), dtype = "complex")
for i in range(n + 1):
if i == 0:
for j in range(l):
bfsize[j] = src[Dec2Bin_Inverse2Dec(j, n)]
else:
tmp = copy.copy(bfsize)
for j in range(l):
pos = j%(pow(2,i))
if pos < pow(2, i - 1):
bfsize[j] = tmp[j] + tmp[j + pow(2, i - 1)] * np.exp(complex(0, -2*np.pi*pos/pow(2,i)))
bfsize[j + pow(2, i - 1)] = tmp[j] - tmp[j + pow(2, i - 1)] * np.exp(complex(0, -2*np.pi*pos/(pow(2,i))))
return bfsize
def Dec2Bin_Inverse2Dec(n, m):
'''
Especially for fft.To find position.
'''
b = bin(n)[2:]
if len(b) != m:
b = "0"*(m-len(b)) + b
b = b[::-1]
return int(b,2)
src = [1,2,3,4,5,6,7,8]
print(fft1(src))
print(np.fft.fft(src))
那既然快速傅里叶变换没问题了,接着也就是要做快速傅里叶逆变换。先来观察两个公式之间的关系
可以发现,如果将DFT算子中的ux换成-ux,并在前乘以1/N,即可以得到IDFT的算子。这里一开始看不是很理解,因为变量一个u一个x混在一起,但后来仔细想,u、x也充其量是一个序号,因为我们是离散的序列。那么只要注意形式为主。可以推导离散反傅里叶变换的公式如下,只需先将F(u)取共轭就可以直接使用FFT算法计算IFFT。
因为要调用我们之前的fft1函数,所以要写在一起,把练手写的dft1删掉之后完整的代码如下:
import numpy as np
import math
import copy
def fft1(src, dst = None):
'''
src: list is better.One dimension.
'''
l = len(src)
n = int(math.log(l,2))
bfsize = np.zeros((l), dtype = "complex")
for i in range(n + 1):
if i == 0:
for j in range(l):
bfsize[j] = src[Dec2Bin_Inverse2Dec(j, n)]
else:
tmp = copy.copy(bfsize)
for j in range(l):
pos = j%(pow(2,i))
if pos < pow(2, i - 1):
bfsize[j] = tmp[j] + tmp[j + pow(2, i - 1)] * np.exp(complex(0, -2*np.pi*pos/pow(2,i)))
bfsize[j + pow(2, i - 1)] = tmp[j] - tmp[j + pow(2, i - 1)] * np.exp(complex(0, -2*np.pi*pos/(pow(2,i))))
return bfsize
def ifft1(src):
for i in range(len(src)):
src[i] = complex(src[i].real, -src[i].imag)
res = fft1(src)
for i in range(len(res)):
res[i] = complex(res[i].real, -res[i].imag)
return res/len(res)
def Dec2Bin_Inverse2Dec(n, m):
'''
Especially for fft.To find position.
'''
b = bin(n)[2:]
if len(b) != m:
b = "0"*(m-len(b)) + b
b = b[::-1]
return int(b,2)
src = [1,2,3,4,5,6,7,8]
print(ifft1(fft1(src)))可以看到结果如下。虚部非常小,可以认为我们写的内容确实是可行有效的。
[1.-1.11022302e-16j 2.+5.72118873e-18j 3.-9.95799250e-17j
4.+2.16323416e-16j 5.+1.11022302e-16j 6.+5.72118873e-18j
7.+9.95799250e-17j 8.-2.27765794e-16j]
至于二维的离散傅里叶变换,是在给定二维数组的每个维度上依次执行一维FFT,并且使用“原位运算”的方法,所以最终得到的结果也是一个二维数组。
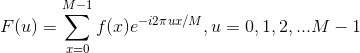
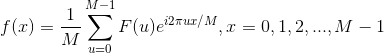
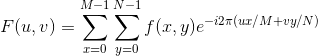







![f(x)=\frac{1}{N}\left [ \sum_{u=0}^{N-1} F^{\ast }(u)W_{N}^{ux} \right ]^{\ast}=\frac{1}{N}\left \{ DFT[F^{\ast}(u)] \right \}^{\ast}](http://img.e-com-net.com/image/info8/437e115808204d76bceee2ee5e112b65.gif)