前言
本次博客是针对面向对象的前三次作业中出现的问题进行的反思与思考。由于大一学习的程序设计与数据结构属于比较基础的课程,且使用C语言实现,在做题过程中总是采用面向过程的方法,使得程序冗长,一main到底。而本学期的前三次作业虽然强调面向对象,但由于理解深刻,往往无法实现真正意义上的高内聚,低耦合,在程序架构,封装性,复杂度方面均出现或多或少的问题。
基于量度分析程序结构
为了用更加量化的数值来体现自己代码有多烂,使用IDEA中的Metrics Reloaded插件来做一些更深入的分析。首先对插件中复杂性测试中的部分指标进行说明:
复杂度指标:
- 循环复杂性 v(G)
穷尽程序每一条路径所需要的实验次数。对于类,有OCavg与WMC两个项目,分别代表类的方法的平均循环复杂度和总循环复杂度。
- 基本复杂性 ev(G)
方法的结构化程度。范围在[1,V(G)]之间,值越大则程序的结构越病态,其计算过程与图的“缩点”有关。
- 方法扩展的循环依懒性 iv(G)
方法与它调用的其他方法的紧密程度。范围在[1,V(G)]之间,值越大则其与其他方法之间联系越紧密
依赖度指标:
- Cyclic
和类直接或间接相互依赖的类的数量。这样的相互依赖容易导致代码可读性较差,调试困难
- Dcy和Dcy*
计算了该类直接依赖的类的数量,*代表包括了间接依赖的类
- Dpt和Dpt*
计算了直接依赖该类的类的数量,*代表包括了间接依赖的类
第一次作业
第一次作业的类图如下:
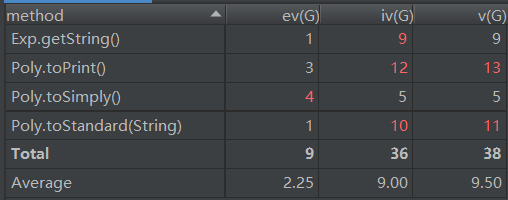
程序结构复杂度如图:
第一次作业由于限制条件较少,且没有想到之后的扩展问题,采用一个正则表达式直接匹配整个表达式的方法。而表达式类的构造函数将字符串处理的工作一并揽下,而没有使用“抽象工厂”的模式。而对面向对象的思想也没有多少领悟,所以把读入,求导,简化,输出当做四个函数来写....而当时没有采用返回一个新Expression类,而是直接在原类上进行修改,在这次作业中后果未体现,不过在第三次作业中尝到恶果。
第二次作业
第二次作业的类图如下:
程序结构的复杂度如图:
本次将幂函数和三角函数分别定义类,并实现了他们的求导和输出方法。按照UML类图可看出,Exp和Tri基本上符合继承的条件,但由于对继承思想的不了解,将其分为两个类,没有实现上层的统一性。而Key类作为HashMap中的Key,代表着该项幂函数指数,正弦函数指数和余弦函数指数,其中重构了必需的equals方法和hashCode方法。而复杂度表只显示了三项数值均不为1的函数,其中getString和toPrint使用了太多的if语句来实现系数为+1,-1,指数为+1等情况的化简,导致v(G)偏大;而toSimply方法使用两个for循环来将指数相同的项合并,导致基本复杂性过大;而toStandard用于识别不同类型的因子,也采用了较多if结构,导致整体复杂度较大。
第三次作业
第三次作业的类图如下(捂脸):
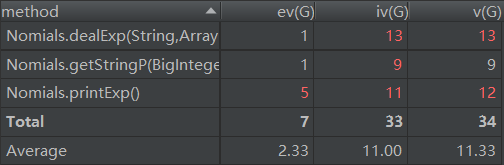
程序结构的复杂度如图:
在第三次作业中,原本按照指导书中的提示构造出了接口——抽象类——因子与运算规则的三层结构,之后建立了表达式树结构。然后由于前期构思花费了大量的时间,导致后来构建输入处理的状态机时遇到问题没有足够的时间进行处理(没有想到之后座谈课上讲述的三层状态机结构),且表达式树的构造存在诸多细节,如:a*b+c此类结构需要将+c放在a*b的*结点上方;嵌套规则的lchild中应有指针指向rchild;在求导过程中如何使用clone方法在不破坏树的结构的前提下构造出新的求导之后的树。在匆忙之下,完成了以上病态的面向对象代码,对此无语置评,只能怪自己对数据结构不够熟悉,对面向对象框架的实现不够了解。此次作业几乎完全面向过程,在一天时间内完成,而在之后的Apply Creation Pattern环节将会把构思好的框架给出。
自己程序的bug
- 第一次作业中,强测没有将正项提前,得分99+;互测过程中,没有考虑\s中包括的\v和\f,被找出的均为此同质bug。
- 第二次作业中,强测仅使用了最简单的sin(x)^2+cos(x)^2=1的化简规则,得分93+;互测过程中,没有被找到bug。
- 第三次作业中,强测由于没有化简,且没有考虑到结尾存在*这一点,得分90+;互测过程中,没有被找到bug
测试他人程序bug方法
测试他人程序时总共采取了三种方式:
- 认真理解他人代码,并找到他人代码的bug
优点:1.认真读取优秀的代码往往能够让自己学到很多东西,从更加精简的语法到更加科学的架构,有时候读下来感觉受益良多,甚至能在读取过程中同时找到自己的bug;
2.真正通过从字里行间分析代码漏洞可以让自己的思维更加缜密,在提升debug能力的同时提高自己提前测出自己bug的能力。
缺点:1.并不是每一份代码都值得细细欣赏,部分同学的代码无条理,无注释,无README,此类三无代码根本无法令人有读取的欲望;
2.无条理的代码令人疑惑不解,导致程序中的错误反而被放过。有时候读完一长串枯燥无味的代码却“掩卷茫然”,一无所获是多么失望的一件事。
- 半自动化构造自己能想到的所有易错样例,一次测试ROOM中所有成员的代码
优点:1.能够以比较快的速度找到尽可能多的bug,同时在测试前通过对代码整体的重新审视,有可能发现自己原本没有考虑过的情况;
2.可以在bug找到之初便确定bug的原因,不会出现怀疑是否为同质bug而不敢提交的情况。
缺点:1.仅仅能够找到自己已经想到而别人没有发现的bug,而不是根据他人代码中的漏洞来设计测试用例
- 使用自动化工具构造样例,一次测试ROOM中所有成员的代码
优点:1.无脑式操作,将脚本编好之后直接后台测试数据,最后人工筛取部分样例进行提交;
2.简单高效,在很短的时间内可以将整个ROOM中所有人的常见bug全部测试出来,奖励分++++。
缺点:1.无知识收获,仅锻炼了写Shell/Python脚本能力,而没有真正获取到他人代码中的精髓之处;
2.无成就感,找到的bug甚至不能确切知道它错在哪里,在提交还是不提交的纠结中度过debug时间(是否提交的是同质bug)。
Applying Creation Pattern
第一次作业
第一次作业中代码基本还是面向过程的,复用性不尽人意。将Factor单独归类,然后用Poly类中采用ArrayList或Hashmap进行连接可以最大限度提高复用性。
第二次作业
第二次作业中除了toString方法基本上没有复用之前代码。此次为了化简方便,放弃了ArrayList而重新写了Hashmap进行存储。将因子分成三角函数类和幂函数类,并实现了求导方法,重载了toString方法。
第三次作业
在完成过程中复用了幂函数类和三角函数类的求导和toString方法,在三角函数类中加入底数(base),并将其设为ArrayList
在作业中采用Expression存Terms,Terms存Factor类的方法,而之后感觉与指导书上说明的tips方法不符,我将设想的另一种框架同时在下方列出。
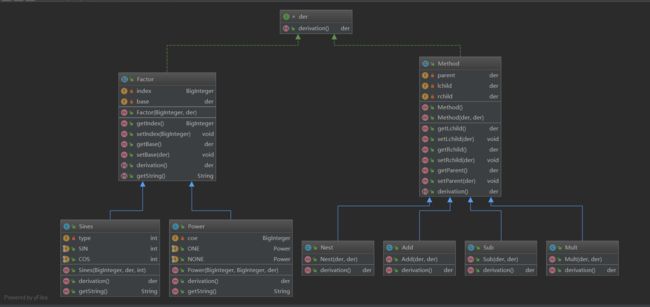
重新思考后的求导接口统一化规范:
该框架为第三次作业构思时搭建而出的,建立Factor和Method两个抽象类。将三角函数中的Sin和Cos都归类到Sines类中,用type属性进行区别;将幂函数和常数归类到Factor类中,将常数视为指数为0的幂函数。而运算规则类中包含四个具体的运算规则,包括Add,Sub,Mult,Nest:
1 public abstract class Method implements der { 2 3 private der parent; 4 private der lchild; 5 private der rchild; 6 7 public Method() { 8 lchild = null; 9 rchild = null; 10 } 11 12 public der getLchild() { 13 return lchild; 14 } 15 16 public void setLchild(der lchild) { 17 this.lchild = lchild; 18 } 19 20 public der getRchild() { 21 return rchild; 22 } 23 24 public void setRchild(der rchild) { 25 this.rchild = rchild; 26 } 27 28 public der getParent() { 29 return parent; 30 } 31 32 public void setParent(der parent) { 33 this.parent = parent; 34 } 35 36 public Method(der lchild, der rchild) { 37 this.parent = null; 38 this.lchild = lchild; 39 this.rchild = rchild; 40 } 41 42 public abstract der derivation(); 43 44 }
1 public class Add extends Method { 2 3 4 public Add(der lchild, der rchild) { 5 super(lchild, rchild); 6 } 7 8 public der derivation() { 9 der temp = new Add(super.getLchild().derivation(), 10 super.getRchild().derivation() 11 ); 12 return temp; 13 } 14 }
1 public class Sub extends Method { 2 3 public Sub(der lchild, der rchild) { 4 super(lchild, rchild); 5 } 6 7 public der derivation() { 8 9 der temp = new Sub(super.getLchild().derivation(), 10 super.getRchild().derivation() 11 ); 12 return temp; 13 } 14 15 }
1 public class Mult extends Method { 2 3 4 public Mult(der lchild, der rchild) { 5 super(lchild, rchild); 6 } 7 8 public der derivation() { 9 der mult1 = new Mult(super.getLchild().derivation(), 10 super.getRchild() 11 ); 12 der mult2 = new Mult(super.getRchild().derivation(), 13 super.getLchild() 14 ); 15 der add1 = new Add(mult1, mult2); 16 return add1; 17 } 18 }
1 public class Nest extends Method { 2 3 4 5 public Nest(der lchild, der rchild) { 6 super(lchild, rchild); 7 } 8 9 public der derivation() { 10 der mult1 = new Mult(super.getLchild().derivation(), 11 super.getRchild().derivation() 12 ); 13 return mult1; 14 } 15 }
由此建立整个表达式树,将三角函数因子与幂函数因子作为叶子节点,将运算规则方法作为根节点和分支节点:
方法如下所示:
Add/Sub节点:Lchild ->加数 Rchild ->加数
Mult节点:Lchild ->乘数 Rchild ->乘数
Nest节点: Lchild ->Sines(base) 其中base指向Rchild Rchild ->嵌套内容的根节点
使用根节点运算规则的求导方法,可直接将整个表达式树进行求导,最后返回一棵新的表达式树。表达式树按照前序遍历的方法可以用getString方法得到最后的输出结果。
对于输入内容的处理,应采用梯度下降的方式,从表达式->项->因子采用三层的小状态机(当时试图采取一层的大型状态机,最后因为同时考虑细节过多而无法完成)。
写在最后
本几次作业以实践的方式让我们了解到:在创建大型工程/不断升级需求的挑战中,面向过程->面向过程的思维转变是不可或缺的。期待之后的面向对象学习与作业,让我能更加感受到JAVA的魅力所在。
1