Reinforcement Learning Exercise 6.9 & 6.10

Exercise 6.9: Windy Gridworld with King’s Moves (programming) Re-solve the windy gridworld assuming eight possible actions, including the diagonal moves, rather than the usual four. How much better can you do with the extra actions? Can you do even better by including a ninth action that causes no movement at all other than that caused by the wind?
Exercise 6.10: Stochastic Wind (programming) Re-solve the windy gridworld task with King’s moves, assuming that the e↵ect of the wind, if there is any, is stochastic, sometimes varying by 1 from the mean values given for each column. That is, a third of the time you move exactly according to these values, as in the previous exercise, but also a third of the time you move one cell above that, and another third of the time you move one cell below that. For example, if you are one cell to the right of the goal and you move left, then one-third of the time you move one cell above the goal, one-third of the time you move two cells above the goal, and one-third of the time you move to the goal.

#==================================================================
# Python3
# Copyright
# 2019 Ye Xiang ([email protected])
#==================================================================

import numpy as np
import copy
import matplotlib.pyplot as mplt_pyplt

ACTION_LEFT = 0
ACTION_UP = 1
ACTION_RIGHT = 2
ACTION_DOWN = 3
ACTION_LEFTUP = 4
ACTION_RIGHTUP = 5
ACTION_RIGHTDOWN = 6
ACTION_LEFTDOWN = 7
ACTION_STAY = 8

ACTIONS_TYPE_4 = 0
ACTIONS_TYPE_8 = 1
ACTIONS_TYPE_9 = 2

class CState:
    def __init__(self, x = 0, y = 0):
        self.X = int(x)
        self.Y = int(y)
    
    def __eq__(self, rhs):
        return self.X == rhs.X and self.Y == rhs.Y

    def __ne__(self, rhs):
        return self.X != rhs.X or self.Y != rhs.Y

class CWindy_gridworld:
    def __init__(self):
        self.__gridworld_width = 0
        self.__gridworld_height = 0
        self.__wind_strength = None
        self.__Q = None
        self.__actions = {}
        self.__epsilon = 0
        self.__alpha = 0
        self.__gamma = 0
        self.__state_start = CState(0, 3)
        self.__state_goal = CState(7, 3)
        self.__time_steps = 0
        self.__records = []
        self.__f_get_next_state = None
        
    def __initialize(self, stochastic_wind, actions_type, epsilon, alpha, gamma = 1):
        self.__gridworld_width = 10
        self.__gridworld_height = 7
        self.__wind_strength = np.zeros((self.__gridworld_width, self.__gridworld_height))
        self.__wind_strength[3:6, :] = 1
        self.__wind_strength[6:8, :] = 2
        self.__wind_strength[8, :] = 1
        self.__actions.clear()
        if(actions_type == ACTIONS_TYPE_4):
            self.__actions = { ACTION_LEFT:(-1, 0), ACTION_UP:(0, 1), ACTION_RIGHT:(1, 0), ACTION_DOWN:(0, -1)}
        elif(actions_type == ACTIONS_TYPE_8):
            self.__actions = {ACTION_LEFT:(-1, 0), ACTION_UP:(0, 1), ACTION_RIGHT:(1, 0), ACTION_DOWN:(0, -1), 
                ACTION_LEFTUP:(-1, 1), ACTION_RIGHTUP:(1, 1), ACTION_RIGHTDOWN:(1, -1), ACTION_LEFTDOWN:(-1, -1)}
        elif(actions_type == ACTIONS_TYPE_9):
            self.__actions = {ACTION_LEFT:(-1, 0), ACTION_UP:(0, 1), ACTION_RIGHT:(1, 0), ACTION_DOWN:(0, -1), 
                ACTION_STAY:(0 ,0), ACTION_LEFTUP:(-1, 1), ACTION_RIGHTUP:(1, 1), ACTION_RIGHTDOWN:(1, -1), ACTION_LEFTDOWN:(-1, -1)}
        else:
            raise TypeError('Invalid action type!')
        self.__Q = np.zeros((self.__gridworld_width, self.__gridworld_height, len(self.__actions)))
        self.__epsilon = epsilon
        self.__alpha = alpha
        self.__gamma = gamma
        self.__time_steps = 0
        self.__records = []
        if stochastic_wind:
            self.__f_get_next_state = self.__get_next_state_stochastic
        else:
            self.__f_get_next_state = self.__get_next_state


    def __get_next_state(self, state, action):
        temp = self.__actions[action]
        X = state.X + temp[0]
        Y = state.Y + temp[1] + self.__wind_strength[state.X][state.Y]
        X = max(0, min(X, self.__gridworld_width - 1))
        Y = max(0, min(Y, self.__gridworld_height - 1))
        return CState(X, Y)

    def __get_next_state_stochastic(self, state, action):
        temp = self.__actions[action]
        X = state.X + temp[0]
        wind_strength = self.__wind_strength[state.X][state.Y]
        Y = state.Y + temp[1] + wind_strength
        if wind_strength != 0:
            Y = Y + np.random.choice([-1, 0, 1])
        X = max(0, min(X, self.__gridworld_width - 1))
        Y = max(0, min(Y, self.__gridworld_height - 1))
        return CState(X, Y)

    def __get_action(self, state):
        if np.random.choice([True, False], p = [1 - self.__epsilon, self.__epsilon]):
            q_max = np.max(self.__Q[state.X][state.Y])
            indices = [i for i, val in enumerate(self.__Q[state.X][state.Y]) if val == q_max]
            return np.random.choice(indices)
        else:
            return np.random.choice(list(self.__actions.keys()))

    def __run_in_episode(self):
        state = copy.copy(self.__state_start)
        action = self.__get_action(state)
        while state != self.__state_goal:
            next_state = self.__f_get_next_state(state, action)
            next_action = self.__get_action(next_state)
            reward = -1 if next_state != self.__state_goal else 0
            Q_s_a = self.__Q[state.X][state.Y][action]
            self.__Q[state.X][state.Y][action] = Q_s_a + self.__alpha * (reward + self.__gamma * self.__Q[next_state.X][next_state.Y][next_action] - Q_s_a)
            state = next_state
            action = next_action            
            self.__time_steps += 1

    def Sarsa_on_policy(self, stochastic_wind = False, episodes = 200, actions_type = ACTIONS_TYPE_4, epsilon = 0.1, alpha = 0.1, gamma = 1):
        self.__initialize(stochastic_wind, actions_type, epsilon, alpha, gamma)
        for i in range(0, episodes):
            self.__run_in_episode()
            self.__records.append(self.__time_steps)
            print('epsode: %d; progress: %.2f'%(i + 1, i / episodes * 100), end='\r')
        print('episode: %d; progress: 100%%' % (episodes))

    @property
    def records(self):
        return self.__records

class CPlot:
    def plot(self, records, title = ''):
        mplt_pyplt.plot(records, np.arange(1, len(records) + 1, 1))
        mplt_pyplt.xlabel('Time steps')
        mplt_pyplt.ylabel('Episodes')
        mplt_pyplt.title(title)
        mplt_pyplt.show()

if __name__ == "__main__":
    wg = CWindy_gridworld()
    plt = CPlot()
    wg.Sarsa_on_policy()
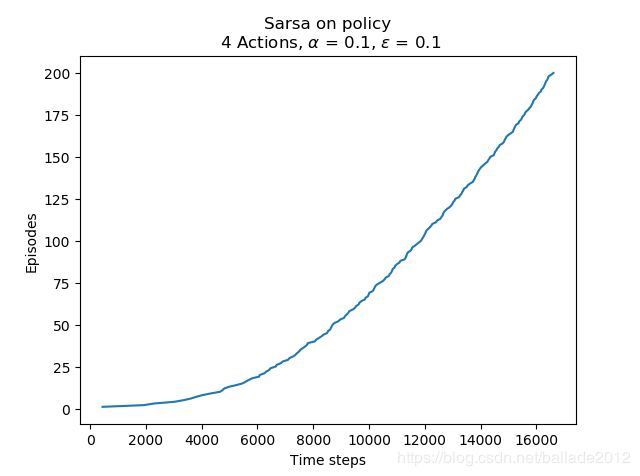
    plt.plot(wg.records, 'Sarsa on policy\n 4 Actions, ' + r'$\alpha$ = 0.1, $\epsilon$ = 0.1')
    wg.Sarsa_on_policy(actions_type = ACTIONS_TYPE_8)
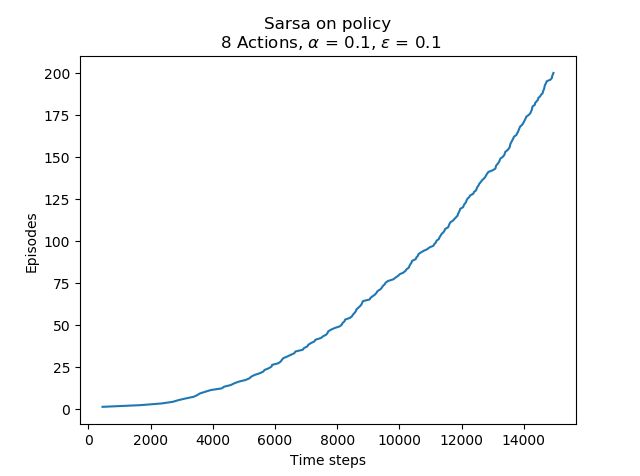
    plt.plot(wg.records, 'Sarsa on policy\n 8 Actions, ' + r'$\alpha$ = 0.1, $\epsilon$ = 0.1')
    wg.Sarsa_on_policy(actions_type = ACTIONS_TYPE_9)
    plt.plot(wg.records, 'Sarsa on policy\n 9 Actions, ' + r'$\alpha$ = 0.1, $\epsilon$ = 0.1')
    wg.Sarsa_on_policy(True)
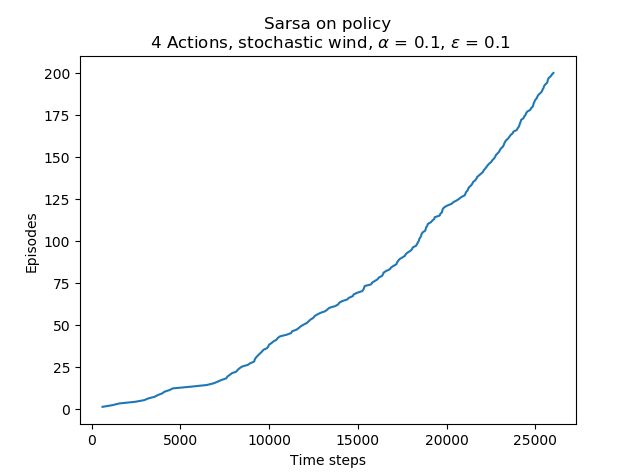
    plt.plot(wg.records, 'Sarsa on policy\n 4 Actions, stochastic wind, ' + r'$\alpha$ = 0.1, $\epsilon$ = 0.1')
    wg.Sarsa_on_policy(True, actions_type = ACTIONS_TYPE_8)
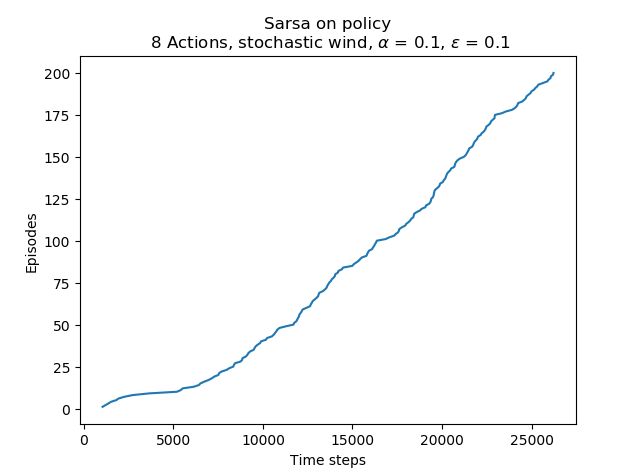
    plt.plot(wg.records, 'Sarsa on policy\n 8 Actions, stochastic wind, ' + r'$\alpha$ = 0.1, $\epsilon$ = 0.1')
    wg.Sarsa_on_policy(True, actions_type = ACTIONS_TYPE_9)
    plt.plot(wg.records, 'Sarsa on policy\n 9 Actions, stochastic wind, ' + r'$\alpha$ = 0.1, $\epsilon$ = 0.1')

Both exercise 6.9 & 6.10 are implemented in the codes above. The results are shown as below:

Figure 1. 4 Actions

Figure 2. 8 Actions

Figure 3. 9 Actions

Figure 4. 4 Actions for stochastic wind

Figure 5. 8 Actions for stochastic wind

Figure 6. 9 Actions for stochastic wind