《大话数据结构》笔记——第7章 图（二）

7.5 图的遍历

图的遍历是和树的遍历类似，我们希望从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历（Traversing Graph）。

树的遍历我们谈到了四种方案，应该说都还好，毕竟根结点只有一个，遍历都是从它发起，其余所有结点都只有一个双亲。可图就复杂多了，因为它的任一顶点都可能和其余的所有顶点相邻接，极有可能存在沿着某条路径搜索后，又回到原顶点，而有些顶点却还没有遍历到的情况。因此我们需要在遍历过程中把访问过的顶点打上标记，以避免访问多次而不自知。具体办法是设置一个访问数组 visited[n]，n 是图中顶点的个数，初值为 0 ，访问过后设置为 1。这其实在小说中常常见到，一行人在迷宫中迷了路，为了避免找寻出路时屡次重复，所以会在路口用小刀刻上标记。

对于图的遍历来说，如何避免因回路陷入死循环，就需要科学地设计遍历方案， 通常有两种遍历次序方案：它们是深度优先遍历和广度优先遍历。

7.5.1 深度优先遍历

深度优先遍历（Depth_First_Search），也有称为深度优先搜索，简称为 DFS。

为了更好的理解深度优先遍历，我们来做一个游戏。

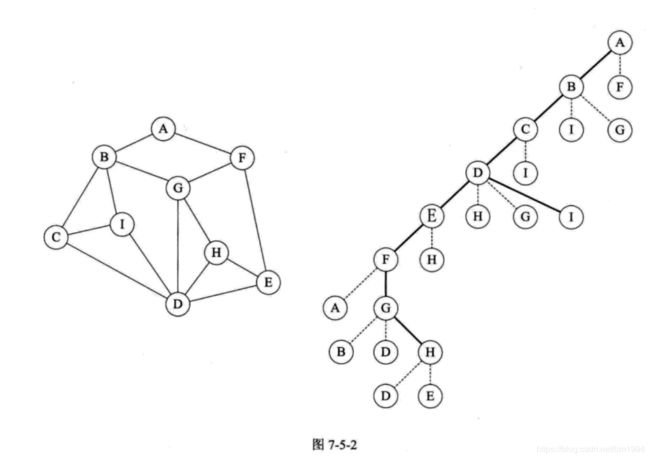
假设你需要完成一个任务，要求你在如图 7-5-2 左图这样的一个迷宫中，从顶点 A开始要走遍所有的图顶点并作上标记，注意不是简单地看着这样的平面图走哦，而是如同现实般地在只有高墙和通道的迷宫中去完成任务。

很显然我们是需要策略的，否则在这四通八达的通道中乱窜，要想完成任务那就只能是碰运气。如果你学过深度优先遍历，这个任务就不难完成了。

首先我们从顶点 A 开始，做上表示走过的记号后，面前有两条路，通向 B 和 F ， 我们给自己定一个原则，在没有碰到重复顶点的情况下，始终是向右手边走，于是走到了 B 顶点。整个行路过程，可参看图 7-5-2 右图。此时发现有三条分支，分別通向顶点 C、I、G，右手通行原则，使得我们走到了 C 顶点。就这样，我们一直顺着右手通道走，一直走到 F 顶点。当我们依然选择右手通道走过去后，发现走回到顶点 A 了，因为在这里做了记号表示已经走过。此时我们退回到顶点 F，走向从右数的第二条通道，到了 G 顶点，它有三条通道，发现 B 和 D 都已经是走过的，于是走到 H ，当我们面对通向 H 的两条通道 D 和 E 时，会发现都已经走过了。

此时我们是否已经遍历了所有顶点呢？没有。可能还有很多分支的顶点我们没有走到，所以我们按原路返回。在顶点 H 处，再无通道没走过，返回到 G，也无未走过通道，返回到 F，没有通道，返回到 E，有一条通道通往 H 的通道，验证后也是走过的，再返回到顶点 D，此时还有三条道未走过，一条条来，H 走过了，G 走过了，I，哦，这是一个新顶点，没有标记，赶快记下来。继续返回，直到返回顶点 A ，确认你已经完成遍历任务，找到了所有的 9 个顶点。

深度优先遍历其实就是一个递归的过程，如果再仔细观察，就会发现其实转换成下图所示后，就像是一棵树的前序遍历，没错， 它就是。它从图中某个顶点 v 出发，访问此顶点，然后从 v 的未被访问的邻接点出发深度优先遍历图，直至图中所有和 v 有路径相通的顶点都被访问到。事实上，我们这里讲到的是连通图，对于非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

如果我们用的是邻接矩阵的方式，则代码如下：

#define MAX 100
#define TRUE  1
#define FALSE 0
typedef int Boolean;	/* Boolean 是布尔类型，其值是 TRUE 或 FALSE */
Boolean visited[MAX];	/* 访问标志的数组 */
/* 邻接矩阵的深度优先递归算法 */ 
void DFS(MGraph G, int i)
{
	int j;
	visited[i] = TRUE;
	printf("%c ", G.vexs[i]); /* 打印頂点，也可以其他操作 */
	for (j = 0; j < G.numVertexes; j++)
	{
		if (G.arc[i][j] == 1 && !visited[j])
		{
			DFS(G, j);	/*对为访问的邻接顶点递归调用*/
		}
	}
 
}
/*邻接矩阵的深度遍历操作*/ 
void DFSTraverse(MGraph G)
{
	int i;
	for (i = 0; i < G.numVertexes; i++)
	{
		visited[i] = FALSE;	/*初始所有顶点状态都是未访问过状态*/
	}
	for (i = 0; i < G.numVertexes; i++)
	{
		if (!visited[i]) /* 对未访问过的顶点调用 DFS , 若是连通图，只会执行一次*/
		{
			DFS(G, i);
		}
	}
							
}

代码的执行过程，其实就是我们刚才迷宫找寻所有顶点的过程。

如果图结构是邻接表结构，其 DFSTraverse 函数的代码是几乎相同的，只是在递归函数中因为将数组换成了链表而有不同，代码如下：

/*邻接表的深度优先递归算法*/ 
void DFS(GraphAdjList GL, int i)
{
	EdgeNode *p; 
	visited[i] = TRUE;
	printf("％c ", GL.adjList[i].data); /* 打印顶点，也可以其他操作 */
	p = GL.adjList[i].firstedge; 
	while (p)
	{
		if (!visited[p->adjvex])
		{
			DFS(GL, p->adjvex); /*对为访问的邻接頂点递归调用*/
		}
		p = p->next;
	}
}
/* 邻接表的深度遍历操作 */
void DFSTraverse(GraphAdjList GL)
{
	int i;
	for (i = 0; i < GL.numVertexes; i++)
	{
		visited[i] = FALSE; /*初始所有顶点狀态都是未访问过狀态*/
	}
	for (i = 0; i < GL.numVertexes; i++)
	{
		if (!visited[i]) /*对未访问过的顶点调用DFS,若是连通图，只会执行一次*/
		{
			DFS(GL, i);
		}
	}
}

对比两个不同存储结构的深度优先遍历算法，对于 n 个顶点 e 条边的图来说，邻接矩阵由于是二维数组，要查找每个顶点的邻接点需要访问矩阵中的所有元素，因此都需要 O(n^2) 的时间。而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边 的数量，所以是 O(n+e) 。显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

对于有向图而言，由于它只是对通道存在可行或不可行，算法上没有变化，是完全可以通用的，这里就不再详述了。

7.5.2 广度优先遍历

广度优先遍历（Breadth_First_SearCh），又称为广度优先搜索，简称 BFS。

如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历了。我们将下图的第一幅图稍微变形，变形原则是顶点 A 放置在最上第一层，让与它有边的顶点 B 、 F 为第二层，再让与 B 和 F 有边的顶点 C 、 I 、 G 、E 为第三层，再将这四个顶点有边的 D 、 H 放在第四层，如下图的第二幅图所示。 此时在视觉上感觉图的形状发生了变化，其实顶点和边的关系还是完全相同的。

有了这个讲解，看代码就非常容易了。以下是邻接矩阵结构的广度优先遍历算法。

/*邻接矩阵的广度遍历算法*/ 
void BFSTraverse(MGraph G)
{
	int i, j;
	Queue Q;
	for (i = 0; i < G.numVertexes; i++)
	{
		visited[i] = FALSE;
	}
	InitQueue(&Q);	/*初始化一辅助用的队列*/
	for (i = 0; i < G.numVertexes; i++)	/* 对每一个顶点做循环 */
	{
		if (!visited[i])	/*若是未访问过就处理*/
		{
			visited[i] = TRUE;	/*设置当前顶点访问过*/
			printf("%c ", G.vexs[i]); /*打印顶点，也可以其他操作*/
			EnQueue(&Q, i);	/*将此顶点入队列*/
			while (!QueueEmpty(Q))/* 若当前队列不为空 */
			{
				DeQueue(&Q, &i);	/*将队中元素出队列，赋值给 i */
				for (j = 0; j < G.numVertexes; j++)
				{
					/*判断其他顶点若与当前顶点存在边且未访问过*/
					if (G.arc[i][j] == 1 && !visited[j])
					{
						visited[j] = TRUE; /*将找到的此顶点标记为已访问*/
						printf("%c ", G.vexs[j]);	/* 打印頂点*/
						EnQueue(&Q, j);	/*将找到的此顶点入队列*/
					}
				}
			}
		}
	}
}

对于邻接表的广度优先遍历，代码与邻接矩阵差异不大，代码如下。

/* 邻接表的广度遍历算法 */
void BFSTraverse(GraphAdjList *GL)
{
	int i;
	EdgeNode *p;
	Queue Q;
	for (i = 0; i < GL->numVertexes; i++)
	{
		visited[i] = FALSE;
	}
	InitQueue(&Q);
	for (i = 0; i < GL->numVertexes; i++)
	{
		if (!visited[i])
		{
			visited[i] = TRUE;
			printf("nc ", GL->adjList[i].data); /* 打印顶点，也可以其他操作 */
			EnQueue(&Q, i);
			while (!QueueEmpty(Q))
			{
				DeQueue(&Q, &i);
				p = GL->adjList[i].firstedge;/* 找到当前顶点边表链表头指针 */
				while (p)
				{
					if (!visited[p->adjvex])	/* 若此顶点未被访问 */
					{
						visited[p->adjvex] = TRUE;
						printf("%c ", GL->adjList[p->adjvex].data);
						EnQueue(&Q, p->adjvex); /* 将此顶点入队列 */
					}
					p = p->next;	/* 指针指向下一个邻接点 */
				}
			}
		}
	}
}

对比图的深度优先遍历与广度优先遍历算法，你会发现，它们在时间复杂度上是一样的，不同之处仅仅在于对顶点访问的顺序不同。可见两者在全图遍历上是没有优劣之分的，只是视不同的情况选择不同的算法。

不过如果图顶点和边非常多，不能在短时间内遍历完成，遍历的目的是为了寻找合适的顶点，那么选择哪种遍历就要仔细斟酌了。深度优先更适合目标比较明确，以找到目标为主要目的的情况，而广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。

7.6 最小生成树

假设你是电信的实施工程师，需要为一个镇的九个村庄架设通信网络做设计，村庄位置大致如图 7-6-1，其中 v0-v8 是村庄，之间连线的数字表示村与村间的可通达的直线距离，比如 v0 至 v1 就是 10 公里（个别如 v0 与 v6，v6 与 v8， v5 与 v7 未测算距离是因为有高山或湖泊，不予考虑）。你们领导要求你必须用最小的成本完成这次任务。你说怎么办？

显然这是一个带权值的图，即网结构。所谓的最小成本，就是 n 个顶点，用 n-1 条边把一个连通图连接起来，并且使得权值的和最小。在这个例子里，每多一公里就多一份成本，所以只要让线路连线的公里数最少，就是最少成本了。

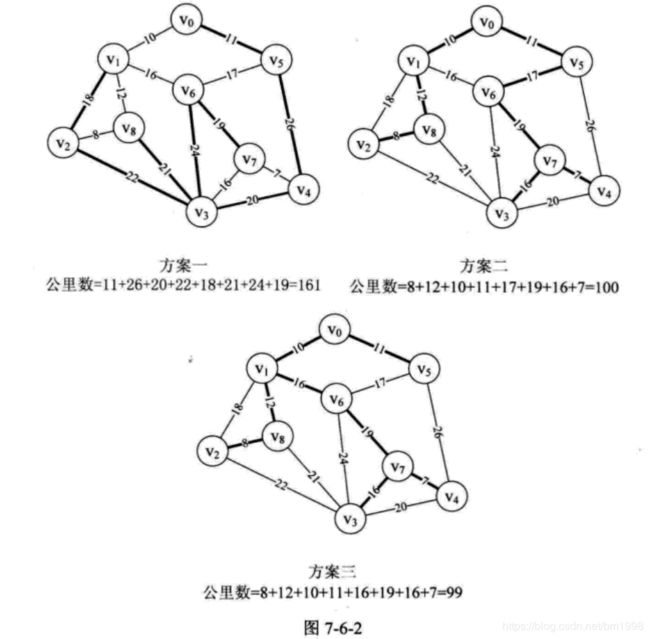
如果你加班加点，没日没夜设计出的结果是如图 7-6-2 的方案一（粗线为要架设线路），我想你离被炒鱿鱼应该是不远了。因为这个方案比后两个方案多出 60% 的成本会让老板气晕过去的。

方案三设计得非常巧妙，但也只以极其微弱的优势对方案二胜出，应该说很是侥幸。我们有没有办法可以精确计算出这种网图的最佳方案呢？答案当然是 Yes。

一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树的 n-1 条边。显然图 7-6-2 的三个方案都是图 7-6-1 的网图的生成树。那么我们把构造连通网的最小代价生成树称为最小生成树（Minimum Cost Spanning Tree）。

找连通网的最小生成树，经典的有两种算法，普里姆算法和克鲁斯卡尔算法。接下来就分别来介绍一下。

7.6.1 普里姆（ Prim ）算法

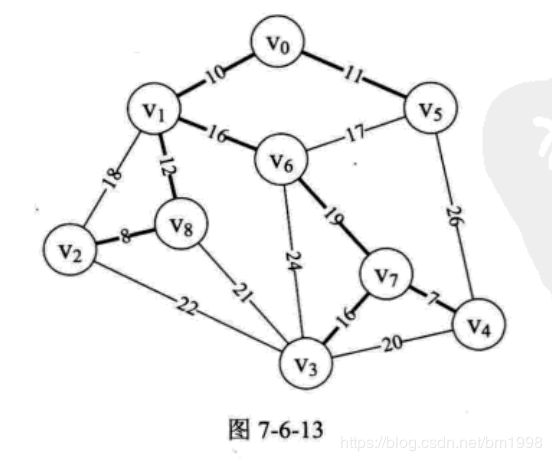
为了能讲明白这个算法，我们先构造图 7-6-1 的邻接矩阵，如图 7-6-3 的右图所示。

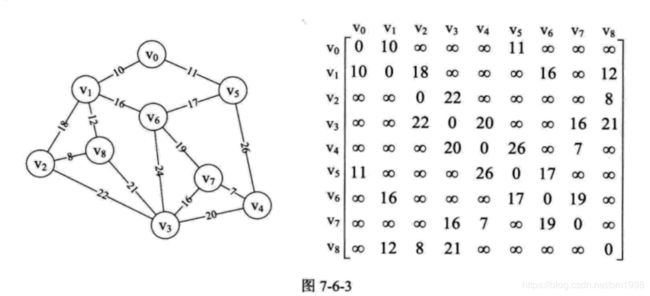
也就是说，现在我们已经有了一个存储结构为 MGragh 的 G（前面邻接矩阵建立的存储结构）。G 有 9 个顶点，它的 arc 二维数组如图 7-6-3 的右图所示。数组中的我们用 65535 来代表 ∞ 。

于是普里姆（ Prim ）算法代码如下，左侧数字为行号。其中 INFINITY 为权值极大值，不妨是 65535，MAXVEX 为顶点个数最大值，此处大于等于 9 即可。现在假设我们自己就是计算机，在调用 MiniSpanTree_Prim 函数，输入上述的邻接矩阵后，看看它是如何运行并打印出最小生成树的。

void MiniSpanTree_Prim(MGraph G) /* Prim 算法生成最小生成树 */
{
	int min, i, j, k;
	int adjvex[MAXVEX];	/* 保存相关顶点下标 */
	int lowcost[MAXVEX]; /* 保存相关顶点间边的权值 */
	lowcost[0] = 0;	/* 初始化第一个权值为 0，即 v0 加入生成树 */
	adjvex[0] = 0;	/* 初始化第一个顶点下标为 0 */
	for (i = 1; i < G.numVertexes; i++) /* 循环除下标为 0 外的全部顶点 */
	{
		lowcost[i] = G.arc[0][i];/* 将 v0 顶点与之有边的权值存入数组 */
		adjvex[i] = 0;	/* 初始化都为 v0 的下标 */ 
	}
	for (i = 1; i < G.numVertexes; i++)
	{
		min = INFINITY; /* 初始化最小权值为 ∞，通常设置为不可能的大数字如 32767、65535 等 */
		j = 1; k = 0;
		while (j < G.numVertexes)	/* 循环全部顶点 */
		{
			if (lowcost[j] != 0 && lowcost[j] < min) 
			{	/* 如果权值不为 0 且权值小于 min */
				min = lowcost[j]; /* 则让当前权值成为最小值*/
				k = j;	/*将当前最小值的下标存入k */
			}
			j++;
		}
		printf(" (%d,*d) ", adjvex[k], k);/*打印当前顶点边中权值最小边*/
		lowcost[k] = 0;/*将当前顶点的权值设置为 0 ,表示此顶点已经完成任务*/
		for (j = 1; j < G.numVertexes; j++) /* 循环所有顶点 */
		{
			if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j]) 
			{	/*若下标为 k 顶点各边权值小于此前这些顶点未被加入生成树权值*/
				lowcost[j] = G.arc[k][j]; /* 将较小权值存入 lowcost */
				adjvex[j] = k;	/* 将下标为 k 的顶点存入adjvex */
			}
		}
	}
}

1. 程序开始运行，我们由第 4〜5 行，创建了两个一维数组 lowcost 和 adjvex , 长度都为顶点个数 9 。它们的作用我们慢慢细说。

2. 第 6〜7 行我们分别给这两个数组的第一个下标位赋值为 0， adjvex[0]=0 其实意思就是我们现在从顶点 v0 开始（事实上，最小生成树从哪个顶点开始计算都无所谓，我们假定从 v0 开始），lowcost[0]=0 就表示 v0 已经被纳入到最小生成树中，之后凡是 lowcost 数组中的值被设置为 0 就是表示此下标的顶点被纳入最小生成树。

3. 第 8〜12 行表示我们读取图 7-6-3 的右图邻接矩阵的第一行数据。将数值赋值给 lowcost 数组，所以此时 lowcost 数组值为 { 0，10，65535，65535，65535，11，65535，65535，65535 } ，而 arjvex 则全部为 0。此时，我们已经完成了整个初始化的工作，准备开始生成。

4. 第 13〜36 行，整个循环过程就是构造最小生成树的过程。

5. 第 15〜16 行，将 min 设置为了一个极大值 65535 ，它的目的是为了之后找到一定范围内的最小权值。j 是用来做顶点下标循环的变量，k 是用来存储最小权值的顶点下标。

6. 第 17〜25 行，循环中不断修改 min 为当前 lowcost 数组中最小值，并用 k 保留此最小值的顶点下标。经过循环后， min=10 , k=1 。注意 19 行 if 判断的 lowcost[ j ] != 0 表示已经是生成树的顶点不参与最小权值的查找。

7. 第 26 行，因 k=1 ，adjvex[1]=0，所以打印结果为（0, 1），表示 v0 至 v1 边为最小生成树的第一条边。如图 7-6-4 所示。

   

8. 第 27 行，此时因 k=1 我们将 lowcost[k]=0 就是说顶点 v1 纳入到最小生成树中。此时 lowcost 数组值为 { 0， 0， 65535， 65535， 65535， 11， 65535， 65535， 65535 } 。

9. 第 28〜35 行，j 循环由 1 至 8 ，因 k=1 ，查找邻接矩阵的第 v1 行的各个权值，与 lowcost 的对应值比较，若更小则修改 lowcost 值，并将 k 值存入 adjvex 数组中。因第 v1 行有 18、16、12 均比 65535 小，所以最终 lowcost 数组的值为： { 0， 0， 18， 65535， 65535， 11， 16， 65535， 12} 。adjvex 数组的值为： { 0， 0， 1， 0， 0， 0， 1， 0， 1} 。这里第 30 行 if 判断的 lowcost [ j ] != 0 也说明 v0 和 v1 已经是生成树的顶点不参与最小权值的比对了。

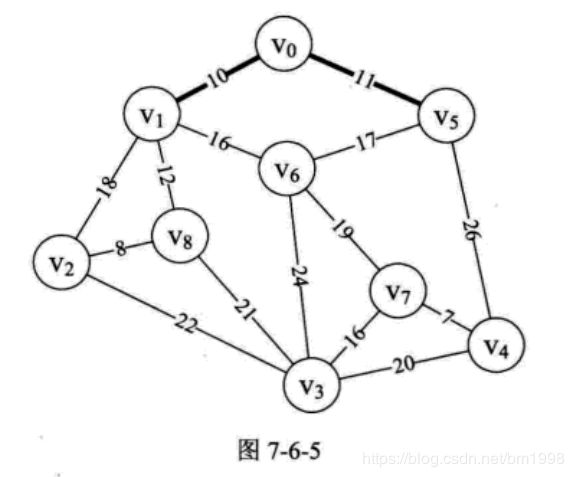
10. 再次循环，由第 15 行到第 26 行，此时 min=11， k=5， adjvex[5]=0。因此打印结构为 ( 0，5 )。表示 v0 至 v5 边为最小生成树的第二条边，如图 7-6-5 所示。

    

11. 接下来执行到 36 行，lowcost 数组的值为： {0， 0， 18， 65535， 26 ， 0， 16， 65535， 12 } 。adjvex 数组的值为： { 0， 0， 1， 0， 5， 0， 1， 0， 1 } 。

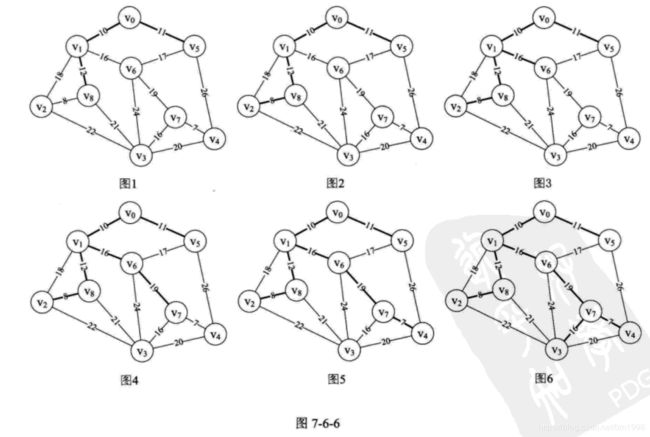
12. 之后，相信大家也都会自己去模拟了。通过不断的转换，构造的过程如图 7-6-6 中图 1〜图 6 所示。

    

下表就是普里姆算法具体执行的步骤：

步骤	U	V-U	lowcost
1	v0	v1,v2,v3,v4,v5,v6,v7,v8	0,10,65535,65535,65535,11,65535,65535,65535
2	v0,v1	v2,v3,v4,v5,v6,v7,v8	0,0,18,65535,65535,11,16,65535,12
3	v0,v1,v5	v2,v3,v4,v6,v7,v8	0,0,18,65535,26,0,16,65535,12
4	v0,v1,v5,v8	v2,v3,v4,v6,v7	0,0,8,21,26,0,16,65535,0
5	v0,v1,v5,v8,v2	v3,v4,v6,v7	0,0,0,21,26,0,16,65535,0
6	v0,v1,v5,v8,v2,v6	v3,v4,v7	0,0,0,21,26,0,0,19,0
7	v0,v1,v5,v8,v2,v6,v7	v3,v4	0,0,0,21,26,0,0,0,0
8	v0,v1,v5,v8,v2,v6,v7,v3	v4	0,0,0,0,26,0,0,0,0
9	v0,v1,v5,v8,v2,v6,v7,v3,v4	NULL	0,0,0,0,0,0,0,0,0

有了这样的讲解，再来介绍普里姆（ Prim ）算法的实现定义可能就容易理解一些。

假设 N= (P,{E}) 是连通网，TE 是 N 上最小生成树中边的集合。算法从 U={u0} (u0∈V) ， TE={} 开始。重复执行下述操作：在所有 u∈U ，v∈V-U 的边 (u,v)∈E 中找一条代价最小的边 (u0,v0) 并入集合 TE，同时 v0 并入 U，直至 U=V 为止。此时 TE 中必有 n-1 条边，则 T= (V,{TE}) 为 N 的最小生成树。

由算法代码中的循环嵌套可得知此算法的时间复杂度为 O(n^2) 。

7.6.2 克鲁斯卡尔（Kruskal）算法

普里姆（ Prim ）算法是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树的。

同样的思路，我们也可以直接就以边为目标去构建，因为权值是在边上，直接去找最小权值的边来构建生成树也是很自然的想法，只不过构建时要考虑是否会形成环路而已。此时我们就用到了图的存储结构中的边集数组结构。以下是 edge 边集数组结构的定义代码：

/* 对边集数组Edge结构的定义 */
typedef struct
{
	int begin; 
	int end; 
	int weight;
}Edge;

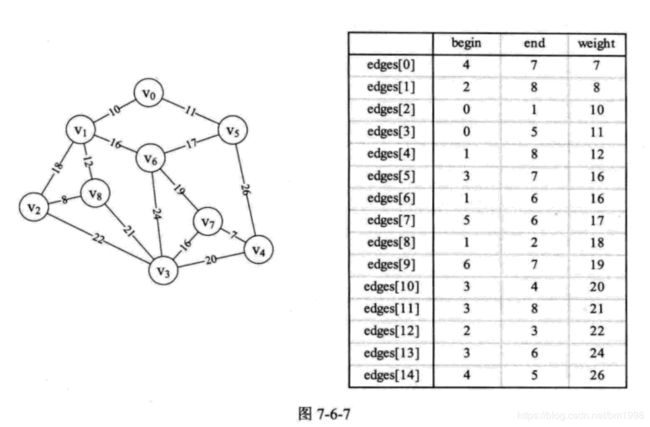
我们将图 7-6-3 的邻接矩阵通过程序转化为图 7-6-7 的右图的边集数组，并且对它们按权值从小到大排序。

于是克鲁斯卡尔（ Kruskal ）算法代码如下，左侧数字为行号。其中 MAXEDGE 为边数量的极大值，此处大于等于 15 即可，MAXVEX 为顶点个数最大值，此处大于等于 9 即可。现在假设我们自己就是计算机，在调用 MiniSpanTree_Kuskal 函数，输入下图的邻接矩阵后，看看它是如何运行并打印出最小生成树的。

void MiniSpanTree_Kruskal(MGraph G) /* Kruskal算法生成最小生成树*/
{
	int i, n, m;
	Edge edges[MAXEDGE];	/* 定义边集数组 */
	int parent [MAXVEX];	/*定义一数组用来利断边与边是否形成环路*/
	for (i = 0; i < G.numVertexes; i++)
		parent[i] = 0;	/*初始化数组值为0	*/
	for (i = 0; i < G.numEdges; i++) /* 循环每一条边 */
	{
		n = Find(parent, edges[i].begin);
		m = Find(parent, edges[i].end);
		if (n != m) /* 假如 n 与 m 不等，说明此边没有与现有生成树形成环路 */
		{
			parent[n] = m; /* 将此边的结尾顶点放入下标为起点的 parent 中，表示此顶点已经在生成树集合中 */ 
			printf(" ( %d, %d) %d ", edges[i].begin, edges[i].end, edges[i].weight);
		}
	}
}

int Find(int *parent, int f)	/* 查找连线顶点的尾部下标 */
{
	while (parent[f] > 0)
		f = parent[f];
	return f;
}

1. 程序开始运行，第 5 行之后，我们省略掉颇占篇幅但却很容易实现的将邻接矩阵转换为边集数组，并按权值从小到大排序的代码，也就是说，在第 5 行开始，我们已经有了结构为 edge ，数据内容是 7-6-7 右图的一维数组 edges 。

2. 第 5〜7 行，我们声明一个数组 parent ，并将它的值都初始化为 0 ，它的作用我们后面慢慢说。

3. 第 8〜17 行，我们开始对边集数组做循环遍历，开始时，i=0 。

4. 第 10 行，我们调用了第 19〜 25 行的函数 Find ，传入的参数是数组 parent 和当前权值最小边 (v4,v7) 的 begin: 4 。因为 parent 中全都是 0 所以传出值使得 n=4 。

5. 第 11 行，同样作法，传入 (v4,v7) 的 end: 7。传出值使得 m=7 。

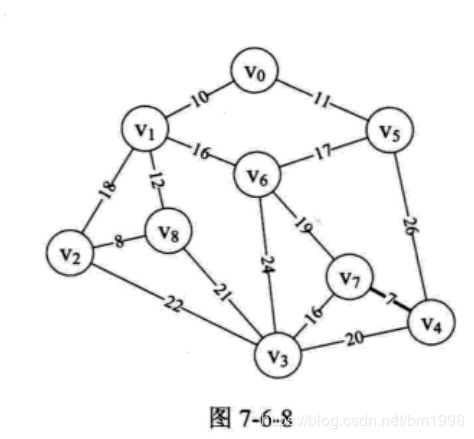
6. 第 12〜16 行，很显然 n 与 m 不相等，因此 parent[4]=7 。此时 parent 数组值为 { 0， 0， 0， 0， 7， 0， 0， 0， 0 }，并且打印得到 “(4, 7) 7” 。此时我们已经将边 (v4,v7) 纳入到最小生成树中，如图 7-6-8 所示。

   

7. 循环返回，执行 10〜16 行，此时 i=1，edge[1] 得到边 (v2,v8) ，n=2 ，m=8 ，parent[2]=8 ，打印结果为 “ (2, 8) 8”，此时 parent 数组值为 { 0， 0， 8， 0， 7， 0， 0， 0， 0 } ，这也就表示边 (v4,v7) 和边 (v2,v8) 已经纳入到最小生成树，如图 7-6-9 所示。

   

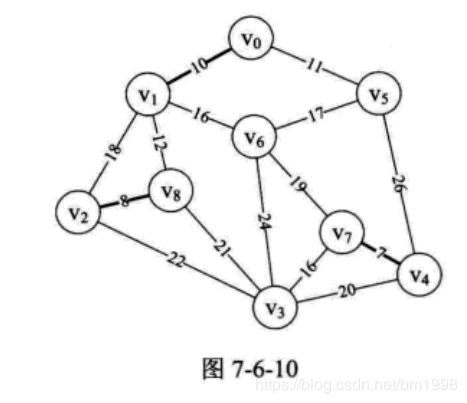
8. 再次执行 10〜16 行，此时 i=2，edge[2] 得到边 (v0,v1)，n=0，m=1，parent[0]=1，打印结果为 “ (0, 1) 10”，此时 parent 数组值为 { 1， 0， 8， 0， 7， 0， 0， 0， 0 } ，此时边 (v4,v7) 、(v2,v8) 和 (v0,v1) 已经纳入到最小生成树，如图 7-6-10 所示。

   

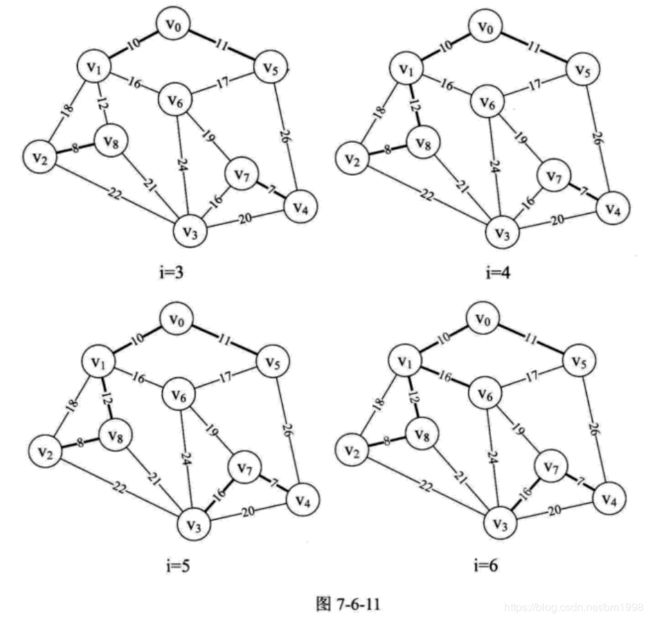
9. 当 i=3 、4 、5 、6 时，分别将边 (v0,v5) 、 (v1,v8) 、 (v3,v7) 、 (v1,v6) 纳入到最小生成树中，如图 7-6-11 所示。此时 parent 数组值为 { 1， 5， 8， 7， 7， 8， 0， 0， 6 } ，怎么去解读这个数组现在这些数字的意义呢？

   

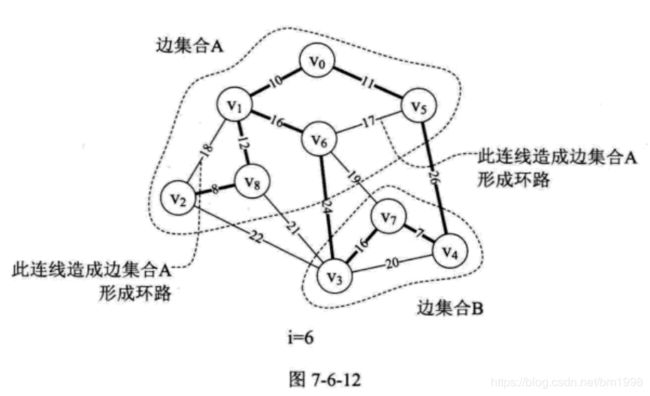
   从图 7-6-11 的最右图 i=6 的粗线连线可以得到，我们其实是有两个连通的边集合 A 与 B 中纳入到最小生成树中的，如图 7-6-12 所示。当 parent[0]=1 ，表示 v0 和 v1 已经在生成树的边集合 A 中。此时将 parent[0]=1 的 1 改为下标，由 parent[1]=5 ，表示 v1 和 v5 在边集合 A 中，parent[5]=8 表示 v5 与 v8 在边集合 A 中，parent[8]=6 表示 v8 与 v6 在边集合 A 中，parent[6]=0 表示集合 A 暂时到头，此时边集合 A 有 v0 、v1 、v5 、v8 、v6 。我们查看 parent 中没有查看的值，parent[2]=8 表示 v2 与 v8 在一个集合中，因此 v2 也在边集合 A 中。再由 parent[3]=7 、 parent[4]=7 和 parent[7]=0 可知 v3 、v4 、v7 在另一个边集合 B 中。

   

10. 当 i=7 时，第 10 行，调用 Find 函数，会传入参数 edges[7].begin=5 。此时第 21 行，parent[5]=8>0，所以 f=8 ，再循环得 parent[8]=6 。因 parent[6]=0 所以 Find 返回后第 10 行得到 n=6 。而此时第 11 行，传入参数 edges[7].end=6 得到 m=6 。此时 n=m ，不再打印，继续下一循环。这就告诉我们，因为边 (v5,v6) 使得边集合 A 形成了环路。因此不能将它纳入到最小生成树中，如图 7-6-12 所示。

11. 当 i=8 时，与上面相同，由于边 (v1,v2) 使得边集合 A 形成了环路。因此不能将它纳入到最小生成树中，如图 7-6-12 所示。

12. 当 i=9 时，边 (v6,v7) ，第 10 行得到 n=6 ，第 11 行得到 m=7 ，因此 parent[6]=7 ，打印 “( 6, 7 ) 19”。此时 parent 数组值为 { 1， 5， 8， 7， 7， 8， 7， 0， 6 } ，如图 7-6-13 所示。

13. 此后边的循环均造成环路，最终最小生成树即为图 7-6-13 所示。

    

好了，我们来把克鲁斯卡尔（ Kruskal ）算法的实现定义归纳一下。

假设 N= (V,{E}) 是连通网，则令最小生成树的初始状态为只有 n 个顶点而无边的非连通图 T={V,{ }} ，图中每个顶点自成一个连通分量。在 E 中选择代价最小的边，若该边依附的顶点落在 T 中不同的连通分量上，则将此边加入到 T 中，否则舍去此边而选择下一条代价最小的边。依次类推，直至 T 中所有顶点都在同一连通分量上为止。

此算法的 Find 函数由边数 e 决定，时间复杂度为 O(loge) ，而外面有一个 for 循环 e 次。所以克鲁斯卡尔算法的时间复杂度为O(eloge)。

对比两个算法，克鲁斯卡尔算法主要是针对边来展开，边数少时效率会非常高， 所以对于稀疏图有很大的优势；而普里姆算法对于稠密图，即边数非常多的情况会更好一些。

7.7 最短路径

在网图和非网图中，最短路径的含义是不同的。由于非网图它没有边上的权值，所谓的最短路径，其实就是指两顶点之间经过的边数最少的路径；而对于网图来说， 最短路径，是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。显然，我们研究网图更有实际意义，就地图来说，距离就是两顶点间的权值之和。而非网图完全可以理解为所有的边的权值都为 1 的网。

7.7.1 迪杰斯特拉（Dijkstra）算法

这是一个按路径长度递增的次序产生最短路径的算法。它的思路大体是这样的。

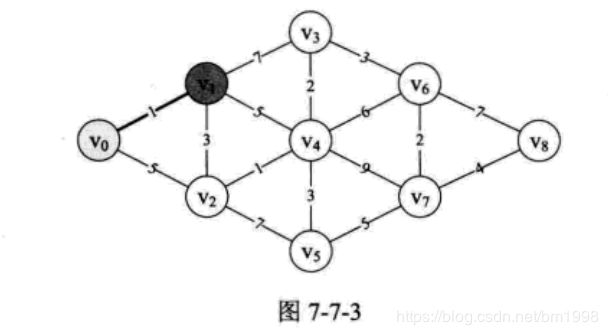
比如说要求图 7-7-3 中顶点 v0 到顶点 v1 的最短距离，没有比这更简单的了，答案就是 1，路径就是直接 v0 连线到 v1 。

由于顶点 v1 还与 v2 、v3 、 v4 连线，所以此时我们同时求得了 v0 --> v1 --> v2 = 1+3 = 4， v0 --> v1 --> v3 = 1+7 = 8 ， v0 --> v1 --> v4 = 1+5 = 6 。

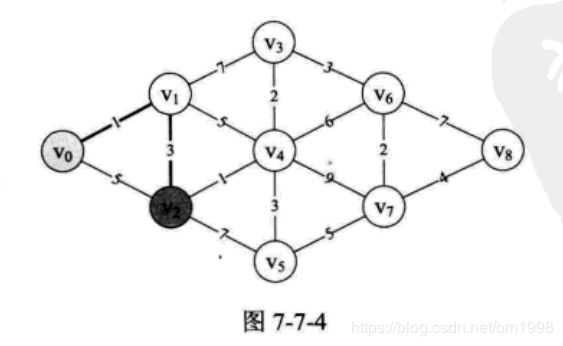
现在，我问 v0 到 v2 的最短距离，如果你不假思索地说是 5 ，那就犯错了。因为边上都有权值，刚才已经有 v0 --> v1 --> v2 的结果是 4 ，比 5 还要小 1 个单位，它才是最短距离，如图 7-7-4 所示。

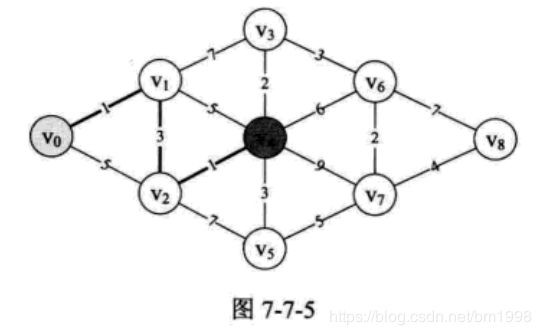
由于顶点 v2 还与 v4 、 v5 连线，所以此时我们求得了 v0 --> v2 --> v4 其实就是 v0 --> v1–> v2 --> v4 = 4+1 = 5， v0 --> v2 --> v5 = 4+7 = 11。这里 v0 --> v2 我们用的是刚才计算出来的较小的 4 。此时我们也发现 v0 --> v1–> v2 --> v4 = 5 要比 v0 --> v1 --> v4 = 6 还要小。所以 v0 到 v4 目前的最小距离是 5 ，如图 7-7-5 所示。

当我们要求 v0 到 v3 的最短距离时，通向 v3 的三条边，除了 v6 没有研究过外，v0 --> v1 --> v3 的结果是 8 ，而 v0 --> v4 --> v3 = 5+2 = 7 。因此，v0 到 v3 的最短距离是 7 ，如图 7-7-6 所示。

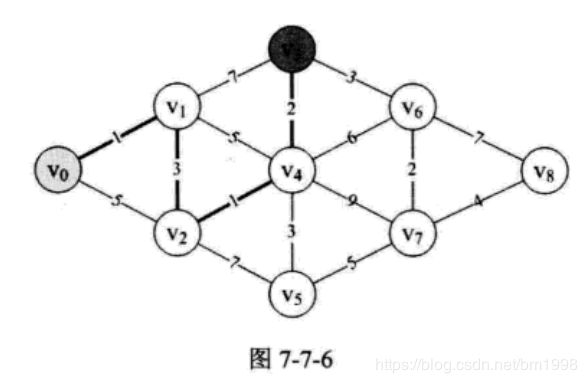
好了，我想你大致明白，这个迪杰斯特拉（ Dijkstra ）算法是如何干活的了。它并不是一下子就求出了 v0 到 v8 的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果。

如果还是不太明白，不要紧，现在我们来看代码，从代码的模拟运行中，再次去理解它的思想。

#define MAXVEX 9 
#define INFINITY 65535
typedef int Pathmatirx[MAXVEX];		/* 用于存储最短路径下标的数组 */
typedef int ShortPathTable[MAXVEX];	/* 用于存储到各点最短路径的权值和 */

/* Dijkstra 算法，求有向网 G 的 v0 顶点到其余顶点 v 最短路径 P[v] ，及带权长度 D[v] */
/* P[v] 的值为前驱顶点下标，D[v] 表示 v0 到 v 的最短路径长度和。 */
void ShortestPath__Dijkstra(MGraph G, int v0, Pathmatirx *P, ShortPathTable *D)
{
	int v, w, k, min;
	int final[MAXVEX];		/* final[w]=1 表示求得顶点 v0 至 v(w) 的最短路径*/
	for (v = 0; v < G.numVertexes; v++)		/* 初始化数据 */
	{
		final[v] = 0;			/* 全部顶点初始化为未知最短路径状态 */
		(*D)[v] = G.matirx[v0][v];		/* 将与 v0 点有连线的顶点加上权值 */
		(*P)[v] = 0;			/* 初始化路径数组 P 为 0 */
	}
	(*D)[v0] = 0;		/* v0 至 v0 路径为 0 */
	final[v0] = 1;		/* v0 至 v0 不需要求路径 */
	/* 开始主循环，每次求得 v0 到某个 v 顶点的最短路径 */
	for (v = 1; v < G.numVertexes; v++)
	{
		min = INFINITY;		/* 当前所知离 v0 顶点的最近距离 */
		for (w = 0; w < G.numVertexes; w++)	/* 寻找离 v0 最近的顶点 */
		{
			if (!final[w] && (*D)[w] < min)
			{
				k = w;
				min = (*D)[w]; /* w 顶点离 v0 顶点更近 */
			}
		}
		final[k] = 1;	/* 将目前找到的最近的顶点置为 1 */
		for (w = 0; w < G.numVertexes; w++)	/* 修正当前最短路径及距离 */
		{
			/* 如果经过 v 顶点的路径比现在这条路径的长度短的话 */
			if (!final[w] && (min + G.matirx[k][w] < (*D)[w]))
			{
				/* 说明找到了更短的路径，修改 D[w] 和 P[w] */
				(*D)[w] = min + G.matirx[k][w];	/* 修改当前路径长度 */
				(*P)[w] = k;
			}
		}
	}
}

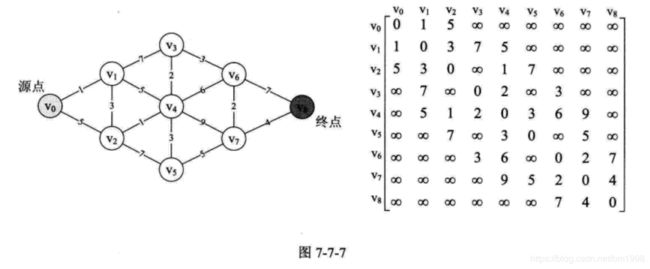
调用此函数前，其实我们需要为图 7-7-7 的左图准备邻接矩阵 MGraph 的 G ，如图 7-7-7 的右图，并且定义参数为 0 。

1. 程序开始运行，第 4 行 final 数组是为了 v0 到某顶点是否已经求得最短路径的标记，如果 v0 到 v(w) 已经有结果，则 final[w]=1 。

2. 第 5-10 行，是在对数据进行初始化的工作。此时 final 数组值均为 0 ，表示所有的点都未求得最短路径。 D 数组为 { 65535， 1， 5， 65535， 65535， 65535， 65535， 65535， 65535 } 。因为 v0 与 v1 和 v2 的边权值为 1 和 5。P 数组全为 0，表示目前没有路径。

3. 第 11 行，表示 v0 到 v0 自身，权值和结果为 0 。D 数组为 { 0， 1， 5， 65535， 65535， 65535， 65535， 65535， 65535 } 。第 12 行，表示 v0 点算是已经求得最短路径，因此 final[0]=1。此时 final 数组为 { 1， 0， 0， 0， 0， 0， 0， 0， 0 } 。此时整个初始化工作完成。

4. 第 13〜33 行，为主循环，每次循环求得 v0 与一个顶点的最短路径。因此 v 从 1 而不是 0 开始。

5. 第 15〜23 行，先令 min 为 65535 的极大值，通过 w 循环，与 D[w] 比较找到最小值 min=1， k=1 。

6. 第 24 行，由 k=1 ，表示与 v0 最近的顶点是 v1，并且由 D[1]=1，知道此时 v0 到 v1 的最短距离是 1 。因此将 v1 对应的 final[1] 设置为 1 。此时 final 数组为 { 1， 1， 0， 0， 0， 0， 0， 0， 0 } 。

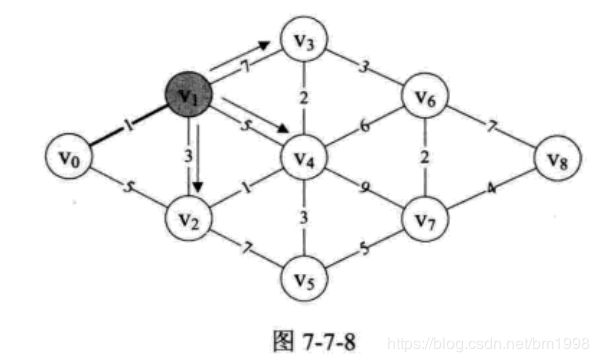
7. 第 25〜32 行是一循环，此循环甚为关键。它的目的是在刚才已经找到 v0 与 v1 的最短路径的基础上，对 v1 与其他顶点的边进行计算，得到 v0 与它们的当前最短距离，如图 7-7-8 所示。因为 min=1 ，所以本来 D[2]=5 ，现在 v0 --> v1 --> v2 = D[2] = min+3 = 4， v0 --> v1 --> v3 = D[3] = min+7 = 8 ， v0 --> v1 --> v4 = D[4] = min+5 = 6 ，因此，D 数组当前值为 { 0， 1， 4， 8， 6， 65535， 65535， 65535， 65535 } 。而 P[2]=1 ， P[3]=1 ，P[4]=1 ，它表示的意思是 v0 到 v2 、 v3 、 v4 点的最短路径它们的前驱均是 v1 。 此时 P 数组值为： { 0， 0， 1， 1， 1， 0， 0， 0， 0 } 。

   

8. 重新开始循环，此时 i=2 。第 15〜23 行，对 w 循环，注意因为 final[0]=1 和 final[1]=1 ，由第 25 行的 !final[w] 可知， v0 与 v1 并不参与最小值的获取。通过循环比较，找到最小值 min=4 ， k=2 。

9. 第 24 行，由 k=2 ，表示已经求出 v0 到 v2 的最短路径，并且由 D[2]=4 ，知道最短距离是 4 。因此将 v2 对应的 final[2] 设置为 1 ，此时 final 数组为： { 1， 1， 1， 0， 0， 0， 0， 0， 0 } 。

10. 第 25〜32 行。在刚才已经找到 v0 到 v2 的最短路径的基础上，对 v2 与其他顶点的边，进行计算，得到 v0 与它们的当前最短距离，如图 7-7-9 所示。因为 min=4 ，所以本来 D[4]=6 ，现在 v0 --> v2 --> v4 = D[4] = min+1 = 5， v0 --> v2 --> v5 = D[5] = min+7 = 11 ，因此，D 数组当前值为：{ 0， 1， 4， 8， 5， 11， 65535， 65535， 65535 } 。而原本 P[4]=1 ，此时 P[4]=2 ， P[5]=2 ，它表示 v0 到 v4 、 v5 点的最短路径它们的前驱均是 v2 。此时 P 数组值为： { 0， 0， 1， 1， 2， 2， 0， 0， 0 } 。

    

11. 重新开始循环，此时 i=3 。第 15〜23 行，通过对 w 循环比较找到最小值 min=5 ，k=4 。

12. 第 24 行，由 k=4 ，表示已经求出 v0 到 v4 的最短路径，并且由 D[4]=5 ，知道最短距离是 5 。因此将 v4 对应的 final[4] 设置为 1 。此时 final 数组为： { 1， 1， 1， 0， 1， 0， 0， 0， 0 } 。

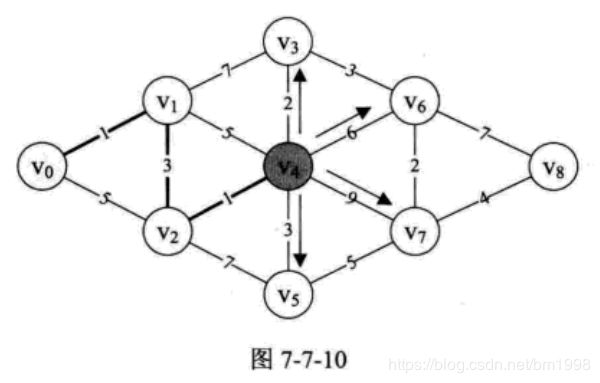
13. 第 25〜32 行。对 v4 与其他顶点的边进行计算，得到 v0 与它们的当前最短距离，如图 7-7-10 所示。因为 min=5 ，所以本来 D[3]=8 ，现在 v0 --> v4 --> v3 = D[3] = min+2 = 7 ，本来 D[5]=11 ，现在 v0 --> v4 --> v5 = D[5] = min+3 = 8，另外 v0 --> v4 --> v6 = D[6] = min+6 = 11 ， v0 --> v4 --> v7 = D[7] = min+9 = 14 ，因此，D 数组当前值为： { 0， 1， 4， 7， 5， 8， 11， 14， 65535 } 。而原本 P[3]=1 ，此时 P[3]=4 ，原本 P[5]=2 ，此时 P[5]=4 ，另外 P[6]=4 ， P[7]=4 ，它表示 v0 到 v3 、 v5 、 v6 、 v7 点的最短路径它们的前驱均是 v4 。此时 P 数组值为：{ 0， 0， 1， 4， 2， 4， 4， 4， 0 } 。

    

14. 之后的循环就完全类似了。得到最终的结果，如图 7-7-11 所示。此时 final 数组为： { 1， 1， 1， 1， 1， 1， 1， 1， 1 } ，它表示所有的顶点均完成了最短路径的查找工作。此时 D 数组为：{ 0， 1， 4， 7， 5， 8， 10， 12， 16 } ，它表示 v0 到各个顶点的最短路径数，比如 D[8]=1+3+1+2+3+2+4=16 。此时的 P 数组为：{ 0， 0， 1， 4， 2， 4， 3， 6， 7 } ， 这串数字可能略为难理解一些。比如 P[8]=7 ，它的意思是 v0 到 v8 的最短路径，顶点 v8 的前驱顶点是 v7 ，再由 P[7]=6 ，表示 v7 的前驱是 v6 ， P[6]=3 ，表示 v6 的前驱是 v3 。这样就可以得到，v0 到 v8 的最短路径为 v8 <-- v7 <-- v6 <-- v3 <-- v4 <-- v2 <-- v1 <-- v0，即 v0 --> v1 --> v2 --> v4 --> v3 --> v6 --> v7 --> v8 。

    

下表就是迪杰斯特拉算法具体执行的步骤：

步骤	S	U
1	v0(0)	v1(1),v2(5),v3(∞),v4(∞),v5(∞),v6(∞),v7(∞),v8(∞)
2	v0(0),v1(1)	v2(4),v3(8),v4(6),v5(∞),v6(∞),v7(∞),v8(∞)
3	v0(0),v1(1),v2(4)	v3(8),v4(5),v5(11),v6(∞),v7(∞),v8(∞)
4	v0(0),v1(1),v2(4),v4(5)	v3(7),v5(8),v6(11),v7(14),v8(∞)
5	v0(0),v1(1),v2(4),v4(5),v3(7)	v5(8),v6(10),v7(14),v8(∞)
6	v0(0),v1(1),v2(4),v4(5),v3(7),v5(8)	v6(10),v7(13),v8(∞)
7	v0(0),v1(1),v2(4),v4(5),v3(7),v5(8),v6(10)	v7(12),v8(17)
8	v0(0),v1(1),v2(4),v4(5),v3(7),v5(8),v6(10),v7(12)	v8(16)
9	v0(0),v1(1),v2(4),v4(5),v3(7),v5(8),v6(10),v7(12),v8(16)	NULL

其实最终返回的数组 D 和数组 P ，是可以得到 v0 到任意一个顶点的最短路径和路径长度的。例如 v0 到 v8 的最短路径并没有经过 v5 ，但我们已经知道 v0 到 v5 的最短路径了。由 D[5]=8 可知它的路径长度为 8 ，由 P[5]=4 可知 v5 的前驱顶点是 v4 ，所以 v0 到 v5 的最短路径是 v0 --> v1 --> v2 --> v4 --> v5 。

也就是说，我们通过迪杰斯特拉（ Dijkstra ）算法解决了从某个源点到其余各顶点的最短路径问题。从循环嵌套可以很容易得到此算法的时间复杂度为 O(n^2) ，尽管有人觉得，可不可以只找到从源点到某一个特定终点的最短路径，其实这个问题和求源点到其他所有顶点的最短路径一样复杂，时间复杂度依然是 O(n^2) 。

可如果我们还需要知道任一顶点到其余所有顶点的最短路径怎么办呢？此时简单的办法就是对每个顶点当作源点运行一次迪杰斯特拉（ Dijkstra ）算法，等于在原有算法的基础上，再来一次循环，此时整个算法的时间复杂度就成了 O(n^3)。

对此，我们现在再来介绍另一个求最短路径的算法——弗洛伊德（ Floyd ），它求所有顶点到所有顶点的时间复杂度也是 O(n^3)，但其算法非常简洁优雅，能让人感觉到智慧的无限魅力。

7.7.2 弗洛伊德（Floyd）算法

为了能讲明白弗洛伊德（ Floyd ）算法的精妙所在，我们先来看最简单的案例。图 7-7-12 的左图是一个最简单的 3 个顶点连通网图。

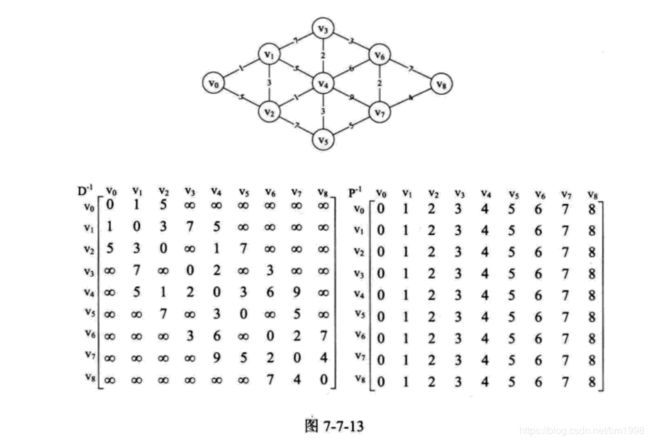
我们先定义两个二维数组 D[3][3] 和 P[3][3] ，D 代表顶点到顶点的最短路径权值和的矩阵。P 代表对应顶点的最小路径的前驱矩阵。在未分析任何顶点之前，我们将 D 命名为 D^(-1)，其实它就是初始的图的邻接矩阵。将 P 命名为 P^(-1) ，初始化为图中所示的矩阵。

首先我们来分析，所有的顶点经过 v0 后到达另一顶点的最短路径。因为只有三个顶点，因此需要查看 v1 --> v0 --> v2 ，得到 D^(-1)[1][0] + D^(-1)[0][2] = 2+1 = 3。 D^(-1)[1][2] 表示的是 v1 --> v2 的权值为 5 ，我们发现 D^(-1)[1][2] > D^(-1)[1][0] + D^(-1)[0][2] ，通俗的话讲就是 v1 --> v0 --> v2 比直接 v1 --> v2 距离还要近。所以我们就让 D^(-1)[1][2] = D^(-1)[1][0] + D^(-1)[0][2] = 3 ，同样的 D^(-1)[2][1] = 3 于是就有了 D^(0) 的矩阵。因为有变化，所以 P 矩阵对应的 P^(-1)[1][2] 和 P^(-1)[2][1] 也修改为当前中转的顶点 v0 的下标 0 ，于是就有了 P^(0) 。也就是说
$$D^0[v][w]=min(D^{-1}[v][w],D^{-1}[v][0]+D^{-1}[0][w])$$
接下来，其实也就是在 D^(0) 和 P^(0) 的基础上继续处理所有顶点经过 v1 和 v2 后到达另一顶点的最短路径，得到 D^(1) 和 P^(1) 、D^(2) 和 P^(2) 完成所有顶点到所有顶点的最短路径计算工作。

如果就用这么简单的图形来讲解代码，大家一定会觉得不能说明什么问题。所以我们还是以前面的复杂网图为例，来讲解弗洛伊德（ Floyd ）算法。

首先我们针对图 7-7-13 的左网图准备两个矩阵 D^(-1) 和 P^(-1) ，D^(-1) 就是网图的邻接矩阵， P^(-1) 初设为 P[i][j] = j 这样的矩阵，它主要用来存储路径。

代码如下，注意因为是求所有顶点到所有顶点的最短路径，因此 Pathmatirx 和 ShortPathTable 都是二维数组。

#define MAXVEX 9 
typedef int Pathmatirx[MAXVEX][MAXVEX]; 
typedef int ShortPathTable[MAXVEX][MAXVEX];
/* Floyd 算法，求网图 G 中各顶点 v 到其余顶点点 w 最短路径 P[v][w] 及带权长度 D[v][w] */ 
void ShortestPath_Floyd(MGraph G, Pathmatirx *P, ShortPathTable *D)
{
	int v, w, k;
	for (v = 0; v < G.numVertexes; ++v)	/* 初始化 D 与 P */
	{
		for (w = 0; w < G.numVertexes; ++w)
		{
			(*D)[v][w] *= G.matirx[v][w]; /* D[v][w] 值即为对应点间的权值 */
			(*P)[v][w] = w;	/* 初始化 P */
		}
	}
	for (k = 0; k < G.numVertexes; ++k)
	{
		for (v = 0; v < G.numVertexes; ++v)
		{
			for (w = 0; w<G.numVertexes; ++w)
			{
				if ((*D)[v][w]>(*D)[v][k] + (*D)[k][w])
				{
					/* 如果经过下标为 k 顶点路径比原两点间路径更短 */
					/* 将当前两点间权值设为更小的一个 */
					(*D)[v][w] = (*D)[v][k] + (*D)[k][w];
					(*P)[v][w] = (*P)[v][k];	/* 路径设置经过下标为 k 的顶点 */
				}
			}
		}
	}
}

1. 程序开始运行，第 4〜11 行就是初始化了 D 和 P ，使得它们成为图 7-7-13 的两个矩阵。从矩阵也得到，v0 --> v1 路径权值是 1，v0 --> v2 路径权值是 5，v0 --> v3 无边连线，所以路径权值为极大值 65535 。

2. 第 12〜25 行，是算法的主循环，一共三层嵌套，k 代表的就是中转顶点的下标。v 代表起始顶点，w 代表结束顶点。

3. 当 k=0 时，也就是所有的顶点都经过 v0 中转，计算是否有最短路径的变化。 可惜结果是，没有任何变化，如图 7-7-14 所示。

   

4. 当 k=1 时，也就是所有的顶点都经过 v1 中转。此时，当 v=0 时，原本 D[0][2]=5 ，现在由于 D[0][1]+D[1][2]=4 。因此由代码的第 20 行，二者取其最小值，得到 D[0][2]=4 ，同理可得 D[0][3]=8 、D[0][4]=6 ，当 v=2、3、4 时，也修改了一些数据，请参考如图 7-7-15 左图中虚线框数据。由于这些最小权值的修正，所以在路径矩阵 P 上，也要作处理，将它们修改为当前的 P[v][k] 值，见代码第 21 行。

   

5. 接下来就是 k=2 一直到 8 结束，表示针对每个顶点做中转得到的计算结果，当然，我们也要清楚，D^(0) 是以 D^(-1) 为基础，D^(1) 是以 D^(0) 为基础，……，D^(8) 是以 D^(7) 为基础，它们是有联系的，路径矩阵 P 也是如此。最终当 k=8 时，两矩阵数据如图 7-7-16 所示。

   

至此，我们的最短路径就算是完成了，你可以看到矩阵第 v0 行的数值与迪杰斯特拉（ Dijkstra ）算法求得的 D 数组的数值是完全相同，都是 { 0， 1， 4， 7， 5， 8， 10， 12， 16 } 。而且这里是所有顶点到所有顶点的最短路径权值和都可以计算出。

那么如何由 P 这个路径数组得出具体的最短路径呢？以 v0 到 v8 为例，从图 7-7-16 的右图第 v8 列，P[0][8]=1，得到要经过顶点 v1 ，然后将 1 取代 0 得到 P[1][8]=2 ，说明要经过 v2，然后将 2 取代 1 得到 P[2][8]=4，说明要经过 v4，然后将 4 取代 2 得到 P[4][8]=3 ，说明要经过 v3，…… ，这样很容易就推导出最终的最短路径值为 v0 --> v1 --> v2 --> v4 --> v3 --> v6 --> v7 --> v8。

求最短路径的显示代码可以这样写：

for (v = 0; v < G.numVertexes; ++v)
{
	for (w = v + l; w < G.numVertexes; w++)
	{
		printf("v%d-v%d weight: %d ", v, w, D[v][w]);
		k = P[v][w];	/* 获得第一个路径顶点下标 */
		printf(" path: %d", v); 	/* 打印源点 */
		while (k != w);	/*如果路径顶点下标不是终点*/
		{
			printf(" -> %d", k);  /* 打印路径顶点 */
			k = P[k][w];	/* 获得下一个路径顶点下标 */
		}
		printf(" -> %d\n", w);/*打印终点*/
	}
	printf("\n");
}

再次回过头来看看弗洛伊德（ Floyd ）算法，它的代码简洁到就是一个二重循环初始化加一个三重循环权值修正，就完成了所有顶点到所有顶点的最短路径计算。几乎就如同是我们在学习 C 语言循环嵌套的样例代码而已。如此简单的实现，真是巧妙之极，在我看来，这是非常漂亮的算法，很可惜由于它的三重循环，因此也是 O(n^3) 时间复杂度。如果你面临需要求所有顶点至所有顶点的最短路径问题时，弗洛伊德（ Floyd ）算法应该是不错的选择。

另外，我们虽然对求最短路径的两个算法举例都是无向图，但它们对有向图依然有效，因为二者的差异仅仅是邻接矩阵是否对称而已。