机器学习的爹——如何成为Logistic的爹

Logistic回归简介

Logistic回归是一种分类模型，是由条件概率分布$P(Y|X)$表示，形式为参数化的Logistic分布，其中，随机变量$X$取值为实数，随机变量$Y$取值为1或0。我们采用监督学习的方法估计模型的参数

1.多个角度理解Logistic

1.1 吴恩达老师的解释

1. 下面是肿瘤分类的例子，目标根据肿瘤大小判断是否是恶性肿瘤。
   
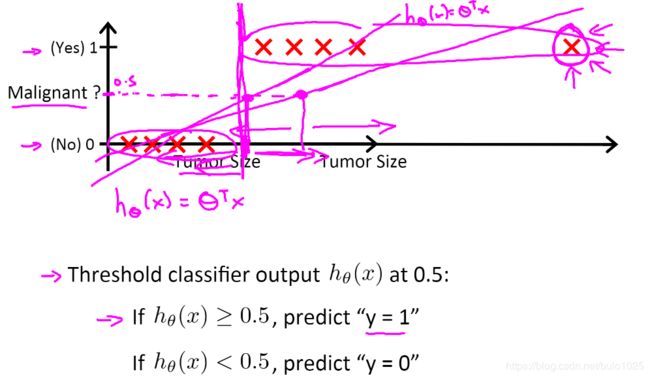
   先利用线性回归模型进行分类，可以发现，这样的一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。最小二乘法会让模型对异常值十分敏感，导致分类结果错误。所以我们的目标是要找一个算法，使得输出值能够在0到1之间。

2. 于是引入了一个新的模型：逻辑回归，将输出变量范围始终控制在0和1之间。构造新的$h_{\theta }\left(x\right)=g\left({\theta }^{T}x\right)$ 其中$x$是特征，$g$代表logistic函数，形式为$g\left(z\right)=\frac{1}{1+e^{-z}}$ 。图像如下图所示：
   
   $h_{\theta }\left(x\right)=P(Y=1|x;\theta )$ 即给定样本数据和参数，样本分类为1的概率。
   $1-h_{\theta }\left(x\right)=P(Y=0|x;\theta )$ 即给定样本数据和参数，样本分类为0的概率。
   例如，如果对于给定的$x$，通过已经确定的参数计算得出预测为1的概率为0.7，则表示有70%的几率y为正向类，相应地y为负向类的几率为1-0.7=0.3。

3. 模型的参数$\theta$到底在求什么，几何意义是什么，吴恩达老师也有所涉及，这就是Decision boundary要了解的内容。
   在逻辑回归中，我们预测：
   当 $h_{\theta }\left(z\right)>=0.5$ 时，预测 $y=1$
   当 $h_{\theta }\left(z\right)<0.5$ 时，预测 $y=0$
   而 $z={\theta }^{T}x$ 即有下式：
   当 ${\theta }^{T}x>=0$ 时，预测 $y=1$
   当 ${\theta }^{T}x<0$ 时，预测 $y=0$
   下图为一个样例，最终求得的参数$\theta$ 是向量[-3,1,1]。可以看出$x_1+x_2=3$这条线成功的将数据点分开。这就是我们所说的Decision boundary
   
   同时，如果要拟合非常复杂的数据分布，可以采用二次方特征：
   
   $h_{\theta }\left(x\right)=g\left({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2\right)$是[-1 0 0 1 1]，模型参数得到的判定边界恰好是圆点在原点且半径为1的圆形。

4. 那么到底如何学习模型的参数$\theta$呢，就是要定义优化目标，即Cost Function.
   有人会觉得，为什么不沿用MSE呢，这里有两个解释：样本这个时候服从伯努利分布，不服从高斯分布；如果在logistic回归中利用MSE方法，则Cost Function是非凸的，不好利用梯度下降法求极值。

每个Cost不再采用MSE，吴恩达并没有解释为什么要这样，但是可以通过直觉验证发现，分别将y = 1和 y = 0带进去，当实际类别与预测类别不一致的时候，Cost是最大的，所以这个函数可以表示我们的Cost。。

后续的步骤就是采用梯度下降法学系参数$\theta$了，后面我们来详细推导。下面我们来看看另外一个大爹李航是怎么讲的。

1.2 李航《统计学习方法》的解释

首先，李航老师引入了一个概念：事件的几率（odds），事件的几率是指该事件发生的概率与改事件不发生概率的比值。如果事件发生的概率是$p$，那么该事件发生的几率是$\frac{p}{1-p}$,同时该事件的对数几率，也叫logit函数是：$$logit(p)=log\frac{p}{1-p}$$根据1.1节中的解释，我们可以理解为，肿瘤恶性的对数几率为：$$log\frac{P(Y=1|X)}{1-P(Y=1|X)}$$可以发现，事件的几率的范围是（0，$+\infty$），经过logit变换后变成了（$-\infty$，$+\infty$)。于是，就想到了，输出Y的对数几率是否可以用x的线性函数表示呢？这个模型就是Logistic模型了，即：$$log\frac{P(Y=1|X)}{1-P(Y=1|X)}=w\cdot x$$同时，这就自然而然的产生了另外一种理解方式，Logistic回归模型可以将线性函数转换为概率：$$P(Y=1|x)=\frac{exp(w\cdot x)}{1+exp(w\cdot x)}$$可以发现线性函数越接近正无穷，概率值就越接近1，线性函数越接近负无穷，概率值就越接近0。
假设$$P(Y=1|x)=h_{\theta }(\mathbf{x}),P(Y=0|x)=1-h_{\theta }(\mathbf{x})$$，则构造的似然函数为$$L(\theta )=\prod _{i=1}^m(h_{\theta }({\mathbf{x}}^i){)}^{y^i}(1-h_{\theta }({\mathbf{x}}^i){)}^{1-y^i}$$求对数似然$$l(\theta )=\log L(\theta )=\sum _{i=1}^m\left[y^{i}log{h}_{\theta }({\mathbf{x}}^i)+(1-y^i)log(1-h_{\theta }({\mathbf{x}}^i)\right]$$

2.模型的参数求解——梯度下降法

基于极大似然估计求解$$\theta ={\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{m}\mathbf{a}\mathbf{x}}_{\theta }l(\theta )$$对${\theta }_j$求偏导有$$\frac{\partial l(\theta )}{\partial {\theta }_j}=\sum _i\left[\frac{y^i}{h_{\theta }({\mathbf{x}}^i)}-\frac{1-y^i}{1-h_{\theta }({\mathbf{x}}^i)}\right]\frac{\partial h_{\theta }({\mathbf{x}}^i)}{\partial {\theta }_j}$$其中$$h_{\theta }({\mathbf{x}}^i)=g({\theta }^T{\mathbf{x}}^i)=\frac{1}{1+e^{-{\theta }^T{\mathbf{x}}^i}}$$$$\frac{\partial h_{\theta }({\mathbf{x}}^i)}{\partial {\theta }_j}=\left[g({\theta }^T{\mathbf{x}}^i)\left(1-g({\theta }^T{\mathbf{x}}^i)\right)\right]\frac{\partial ({\theta }^T{\mathbf{x}}^i)}{\partial {\theta }_j}=\left[g({\theta }^T{\mathbf{x}}^i)\left(1-g({\theta }^T{\mathbf{x}}^i)\right)\right]{\mathbf{x}}_j^i$$带回上式有$$\frac{\partial l(\theta )}{\partial {\theta }_j}=\sum _i\left[\frac{y^i}{g({\theta }^T{\mathbf{x}}^i)}-\frac{1-y^i}{1-g({\theta }^T{\mathbf{x}}^i)}\right]g({\theta }^T{\mathbf{x}}^i)\left(1-g({\theta }^T{\mathbf{x}}^i)\right){\mathbf{x}}_j^i$$$$\frac{\partial l(\theta )}{\partial {\theta }_j}=\sum _i\left[y^i-g({\theta }^T{\mathbf{x}}^i)\right]{\mathbf{x}}_j^i$$根据梯度下降法的更新规则，参数更新公式为：$${\theta }_j:={\theta }_j+\alpha \frac{\partial l(\theta )}{\partial {\theta }_j}={\theta }_j+\alpha \sum _i\left[y^i-g({\theta }^T{\mathbf{x}}^i)\right]{\mathbf{x}}_j^i$$注意这里是求最大值，所以参数是往正梯度方向更新。