【数据压缩】DPCM 压缩系统的实现和分析
一.实验原理
1.预测编码的基本原理
由于信源的相邻符号通常是相关的,利用信源相邻之间的相关性。根据某一模型利用以往的样本值对新样本进行预测,然后将样本的实际值与其预测值相减得到一个误差值,最后对这个误差值进行编码。
如果这个模型足够好,且样本序列在时间上相关性较强,则误差信号的幅度将远远小于原始信号,从而得到较大的数据压缩。
2.DPCM
DPCM是差分预测编码调制的缩写,是比较典型的预测编码系统。在DPCM中,需要注意的是预测器输入的是预测器的输入是已经编码的样本。因为在解码端,同样无法得到原始样本,只能得到存在误差的样本。因此,在DPCM编码器中实际内嵌了一个解码器,如编码器中虚线框中所示。
在一个DPCM系统中,有两个因素需要设计:预测器与量化器。理想情况下,预测器和量化器应该联合设计。但在实际中,采用一种次优的设计方法:分别进行线性预测器和量化器的优化设计。下图则为DPCM编码端与解码端的图示:
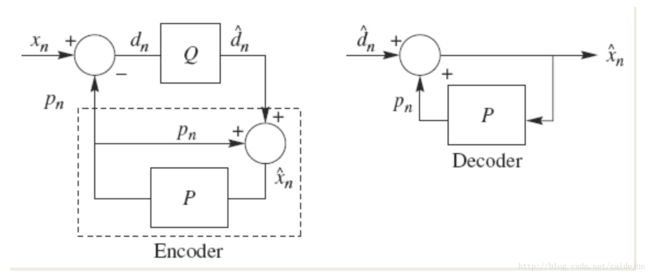
在本次实验中,采用的是固定预测器和均匀量化器。预测器采用的是左侧量化,对于图像中处于最左侧的一列像素,前面没有像素可以预测,则用预测灰度值的平均值128进行量化。
二.代码分析
int limit(int x)
{
if(x>255) return 255;
if(x<0) return 0;
return x;
}
......
qn = (int *)malloc(Info_header.biWidth*Info_header.biHeight*sizeof(int));
q = (unsigned char *)malloc(Info_header.biWidth*Info_header.biHeight);
rebuild = (unsigned char *)malloc(Info_header.biWidth*Info_header.biHeight);
int scale = 512 / (1 << Qbits);
for (int i = 0; i < Info_header.biHeight; i++)
{
qn[i*Info_header.biWidth ] = y_buf[i*Info_header.biWidth ] - 128;
qn[i*Info_header.biWidth ] = qn[i*Info_header.biWidth ] +1/ scale;
rebuild[i*Info_header.biWidth + j] = limit(qn[i*Info_header.biWidth + j] * scale + 128);
q[i*Info_header.biWidth + j] = qn[i*Info_header.biWidth + j] +127;
for (int j = 1; j < Info_header.biWidth; j++)//从第二列开始进入for循环
{
qn[i*Info_header.biWidth + j] = y_buf[i*Info_header.biWidth + j] - rebuild[i*Info_header.biWidth + j - 1];
qn[i*Info_header.biWidth + j] = qn[i*Info_header.biWidth + j]+1 / scale;
rebuild[i*Info_header.biWidth + j] = limit(qn[i*Info_header.biWidth + j] * scale + rebuild[i*Info_header.biWidth + j - 1]);
q[i*Info_header.biWidth + j] = qn[i*Info_header.biWidth + j] +127;
}
}处理程序在实验二BMP2YUV基础上进行即可,其中y_buf数组中已存储着图像的灰度值,作为编码器的输入。scale为量化因子,以4bit量化为例子,因为1<<=16,scale = 512/16=32。qn值除以32后,取值范围中共16位可选电平,符合16bit的量化要求。
由于像素灰度值的取值范围为0~255,任意两个像素的灰度值之差为-255~255,所以定义量化误差qn的数据类型为int类型;另外定义了一个字节大小的量化误差数组“q”,用于接受变换后的qn数据。假设进行8bit量化,而qn的可能位长为9bit,在量化时,若直接将其除于2,由于除法直接向下取整,范围变为-127~127,量化间隔仅有255个<2^8,所以量化语句写成:
qn[i*Info_header.biWidth + j] = qn[i*Info_header.biWidth + j]+1 / scale;
在qn原值加一再除以量化因子,则量化后范围变为-127~128,qn+127=q。q的取值范围则为0~255,符合8bit 256个量化级的要求。
在编码端重建图像时,应注意重建值有可能超过0~255的灰度区间,利用limit(int x)进行限制其取值。
三.实验结果
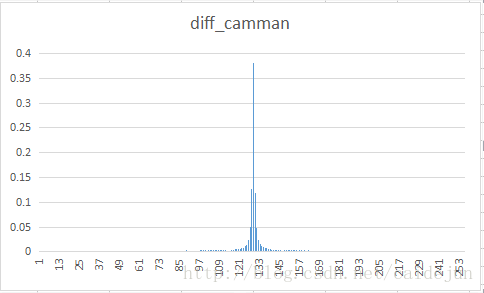
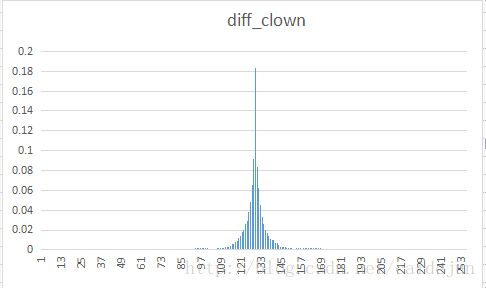
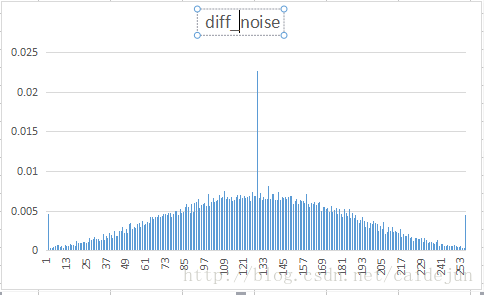
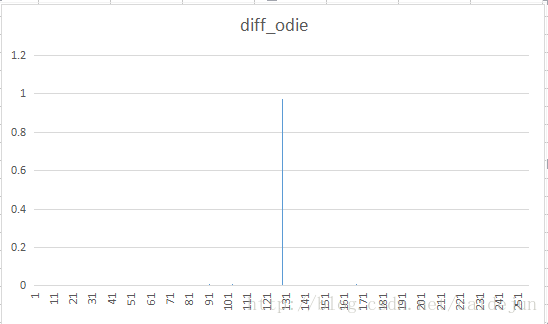
将八幅不同类型的样图进行DPCM变换,观测其重建图像,与差分数据的显示效果。对差分文件进行Huffman 编码,将其符号的分布统计得到下表结果。观测统计结果,得到结论:进行DPCM变换后,由于传输的是原值与预测值的一个差值,这个数值往往比较小,由于程序中将数值上抬127。与图标中128左右的概率分布较多相符。
| 原始图像 | 重建图像 | 差分图像 | 符号分布 |
|---|---|---|---|
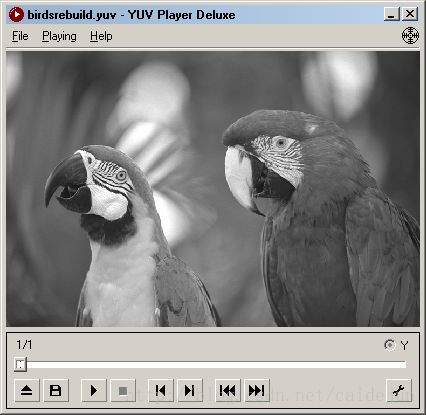 |
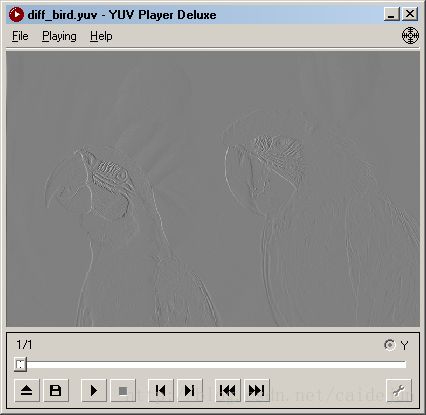 |
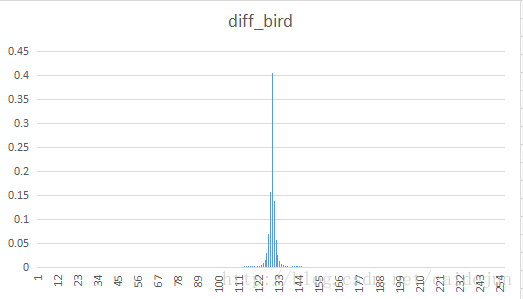 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
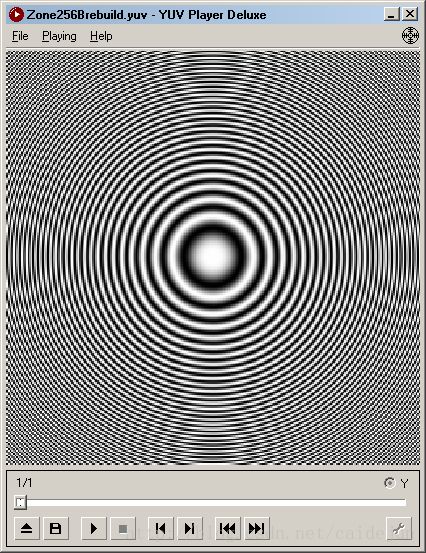 |
 |
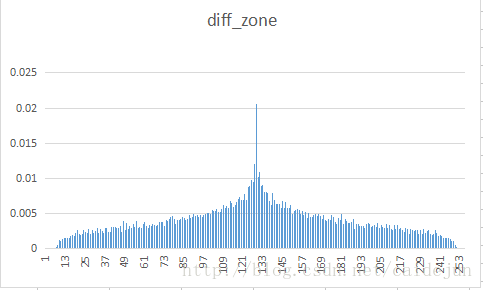 |
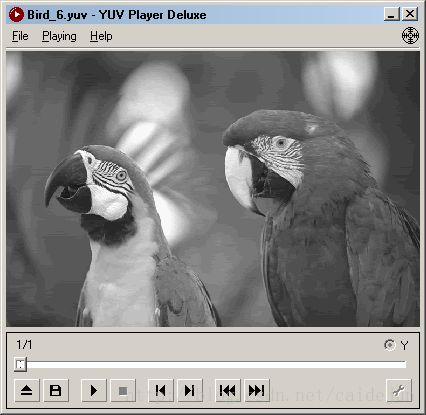
| 8bit量化 | 6bit量化 | 4bit量化 |
|---|---|---|
 |
 |
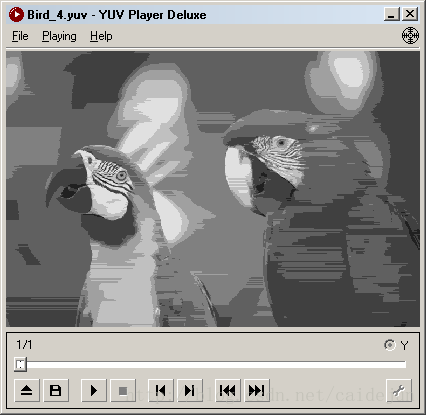 |
压缩性能比较:
| 文件名称 | 源文件大小 | 普通huffman变换后大小 | 压缩比 | DPCM+huffman后大小 | 压缩比 |
|---|---|---|---|---|---|
| birds.bmp | 384kb | 304kb | 1.26 | 148kb | 2.59 |
| camman.bmp | 64kb | 50kb | 1.28 | 32kb | 2.00 |
| clown.bmp | 64kb | 54kb | 1.18 | 39kb | 1.64 |
| fruit.bmp | 64kb | 54kb | 1.18 | 34kb | 1.88 |
| lena.bmp | 64kb | 53kb | 1.20 | 37kb | 1.73 |
| noise.bmp | 64kb | 54kb | 1.18 | 63kb | 1.01 |
| odie.bmp | 64kb | 10kb | 6.4 | 9kb | 7.11 |
| zone.bmp | 64kb | 55kb | 1.16 | 64kb | 1 |
(源文件格式为:从bmp中提取灰度值转换的yuv)
由实验结果:空间冗余较大的图像,如odie.bmp,经过dpcm+熵编码会得到较大的压缩效率;而对应的空间冗余较少的图像,极端的如噪声分布图像 noise.bmp,经过dcpm+熵编码,依旧得不到很高的压缩比。这也符合霍夫曼编码规律,概率分布越集中,则压缩效率越高。综上,利用DPCM进行预测编码时,空间冗余越大,压缩效率越高。