折半查找、插值查找和斐波那契查找
一、折半查找
1、折半查找:折半查找又称为二分查找。前提是线性表中的记录必须是关键码有序,线性表必须采用顺序存储。其基本思想就是在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的坐半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,则查找失败为止。注:这里是指以从小到大的顺序排列的。
2、实例分析
比如有一个有序表数组[1,3,5,7,9,11,13,15,17,19,21],它是按照从小到大的顺序来进行排列的,现在需要在该有序表中查找元素19,步骤如下:
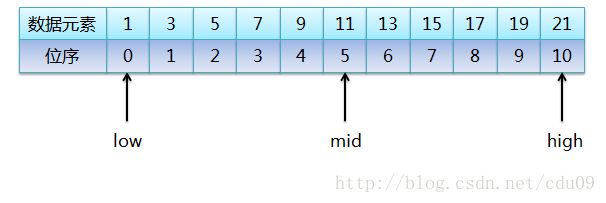
- 首先设置两个指针low和high,分别指向数据集合的第一个数据元素1(位序为0)和最后一个数据元素21(位序为10),然后把整个数据集合长度分成两半,并用一个指针指向它们的临界点,所以定义指针mid指向了中间元素11(位序5),也就是说mid=(high+low)/2,其中high和low都代表所指向的元素的位序,如下图:
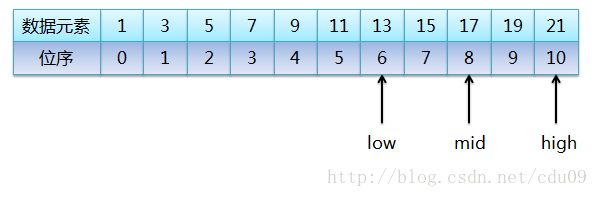
- 接着,将mid所指向的元素(11)与待查找元素(19)进行比较,因为19大于11,说明待查找的元素(19)一定位于mid和high之间。所以继续折半,则low = mid+1,而mid = (low+high)/2,结果如下图:
- 接着,又将mid所指向的元素(17)与待查找元素(19)进行比较,由于19大于17,所以继续折半,则low = mid+1,而mid = (low+high)/2,结果如下图:
- 最后,又将mid所指向的元素(19)与待查找元素(19)进行比较,结果相等,则查找成功,返回mid指针指向的元素的位序。
3、使用递归实现折半查找
/**************************************************************/
/** 折半查找 **/
/**************************************************************/
#include
/**
* 递归实现折半查找,查找成功返回所在数组下标,否则返回-1
* @param data:数据元素所在数组
* @param low:起始下标
* @param high:结束下标
* @param searchValue:待查找元素值
*/
int BinarySearch_Recursion(int data[], int low, int high, const int searchValue)
{
int mid;
if (low > high)
{
return -1;
}
mid = (low + high) / 2;
if (data[mid] == searchValue)
{
return mid;
}
if (data[mid] > searchValue)
{
high = mid - 1;
BinarySearch_Recursion(data, low, high, searchValue);
}
if (data[mid] < searchValue)
{
low = mid + 1;
BinarySearch_Recursion(data, low, high, searchValue);
}
}
int main()
{
int data[] = {1,3,5,7,9,11,13,15,17,19,21};
int index = BinarySearch_Recursion(data, 0, 10, 19);
printf("%d\n", index);
return 0;
}
/**************************************************************/
/** 折半查找 **/
/**************************************************************/
#include
/**
* 迭代法实现折半查找,查找成功返回所在数组下标,否则返回-1
* @param data:数据元素所在数组
* @param length:数组长度
* @param searchValue:待查找元素值
*/
int BinarySearch_Iterator(int data[], int length, int searchValue)
{
int low, high, mid;
low = 0;
high = length - 1;
while (low <= high)
{
mid = (low + high) / 2;
if (data[mid] == searchValue)
{
return mid;
}
if (data[mid] < searchValue)
{
low = mid + 1;
}
if (data[mid] > searchValue)
{
high = mid - 1;
}
}
return -1;
}
int main()
{
int data[] = {1,3,5,7,9,11,13,15,17,19,21};
int index = BinarySearch_Iterator(data, 11, 19);
printf("%d\n", index);
return 0;
} 5、时间复杂度
将该有序表的查找过程绘制成一棵二叉树,如下,从图上来看,如果查找的关键字是不中间记录11的话,折半查找等于是把静态有序查找表分成了两棵子树,即查找结果只需要找其中一半数据记录即可,等于是把工作量少了一半,如此反复。根据二叉树的性质"具有n个结点的完全二叉树的深度为⌊log2n⌋+1",虽然尽管折半查找判定二叉树并不是完全二叉树,但是由该性质可以推导得出,最坏情况是查找到关键字或查找失败的次数为⌊log2n⌋+1,而最好情况就是1了,所以折半查找的时间复杂度为O(log2n)。但是由于折半查找的前提条件是需要有序表顺序存储,对于比较稳定的查找表来说,排列一次就不需要再频繁判续,用折半查找来进行查找就比较适合,但是对于需要频繁执行插入或删除操作的数据集来说,需要经常维护有序的排序,所以对于这种情况下折半查找是不适合的。
二、插值查找
1、从折半查照中可以看出,折半查找的查找效率还是不错的。可是为什么要折半呢?为什么不是四分之一、八分之一呢?打个比方,在牛津词典里要查找“apple”这个单词,会首先翻开字典的中间部分,然后继续折半吗?肯定不会,对于查找单词“apple”,我们肯定是下意识的往字典的最前部分翻去,而查找单词“zero”则相反,我们会下意识的往字典的最后部分翻去。所以在折半查找法的基础上进行改造就出现了插值查找法,也叫做按比例查找。所以插值查找与折半查找唯一不同的是在于mid的计算方式上,它的计算方式为:
mid = low + (high - low) * (searchValue - data[low]) / (data[high] - data[low])
2、时间复杂度
插值查找的时间复杂度也是O(log2n),但是对于数据集合较长,且关键字分布比较均匀的数据集合来说,插值查找的算法性能比折半查找要好,其它的则不适用。
三、斐波那契查找
1、斐波那契查找也叫做黄金分割法查找,它也是根据折半查找算法来进行修改和改进的。
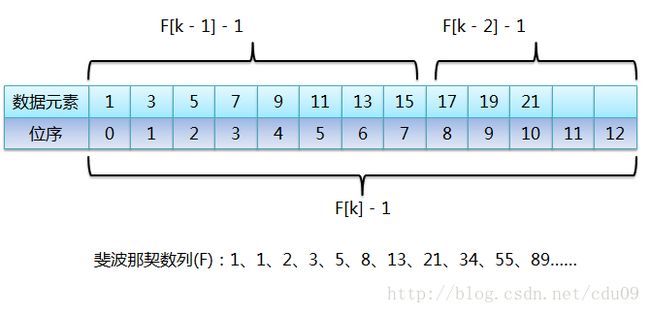
2、对于斐波那契数列:1、1、2、3、5、8、13、21、34、55、89……(也可以从0开始),前后两个数字的比值随着数列的增加,越来越接近黄金比值0.618。比如这里的89,把它想象成整个有序表的元素个数,而89是由前面的两个斐波那契数34和55相加之后的和,也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段,那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618,假如要查找的元素在前半段,那么继续按照斐波那契数列来看,55 = 34 + 21,所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段,继续查找,如此反复,直到查找成功或失败,这样就把斐波那契数列应用到查找算法中了。如下图:
从图中可以看出,当有序表的元素个数不是斐波那契数列中的某个数字时,需要把有序表的元素个数长度补齐,让它成为斐波那契数列中的一个数值,当然把原有序表截断肯定是不可能的,不然还怎么查找。然后图中标识每次取斐波那契数列中的某个值时(F[k]),都会进行-1操作,这是因为有序表数组位序从0开始的,纯粹是为了迎合位序从0开始。所以用迭代实现斐波那契查找算法如下:
/********************************************************************/
/** 斐波那契查找 **/
/********************************************************************/
#include
#define FIB_MAXSIZE 100
/**
* 生成斐波那契数列
* @param fib:指向存储斐波那契数列的数组的指针
* @param size:斐波那契数列长度
*/
void ProduceFib(int *fib, int size)
{
int i;
fib[0] = 1;
fib[1] = 1;
for (i = 2; i < size; i++)
{
fib[i] = fib[i - 1] + fib[i - 2];
}
}
/**
* 斐波那契查找,查找成功返回位序,否则返回-1
* @param data:有序表数组
* @param length:有序表元素个数
* @param searchValue:待查找关键字
*/
int FibonacciSearch(int *data, int length, int searchValue)
{
int low, high, mid, k, i, fib[FIB_MAXSIZE];
low = 0;
high = length - 1;
ProduceFib(fib, FIB_MAXSIZE);
k = 0;
// 找到有序表元素个数在斐波那契数列中最接近的最大数列值
while (high > fib[k] - 1)
{
k++;
}
// 补齐有序表
for (i = length; i <= fib[k] - 1; i++)
{
data[i] = data[high];
}
while (low <= high)
{
mid = low + fib[k - 1] - 1; // 根据斐波那契数列进行黄金分割
if (data[mid] == searchValue)
{
if (mid <= length - 1)
{
return mid;
}
else
{
// 说明查找得到的数据元素是补全值
return length - 1;
}
}
if (data[mid] > searchValue)
{
high = mid - 1;
k = k - 1;
}
if (data[mid] < searchValue)
{
low = mid + 1;
k = k - 2;
}
}
return -1;
}
int main()
{
int data[] = {1,3,5,7,9,11,13,15,17,19,21};
int index = FibonacciSearch(data, 11, 19);
printf("%d\n", index);
return 0;
}