理解 Manacher's Algorithm(马拉车算法)——最长回文子串问题
文章目录
- 马拉车算法(Manacher's Algorithm)
- 1. 改造字符串
- 2. 辅助数组 R[]
- 3. 计算 R[i]
- 求字符串 S 的回文子串数量
- 参考资料
通常的回文串匹配方法:以某个字符为中心,依次向两边匹配。这样有一个问题是,当回文串长度分别为奇数和偶数时,不方便统一处理。马拉车算法的核心思想是利用已经计算过的回文串,并且根据对称性减少匹配次数。另外对字符串进行特殊处理,消除回文串长度奇偶性可能造成的影响。
马拉车算法(Manacher’s Algorithm)
1. 改造字符串
在字符串 S 的相邻字符之间、字符串首部和尾部都插入一个特殊标记字符(以 '#' 为例)。例如,S = "babad" 变为 T = "#b#a#b#a#d#" 。目的是 统一处理回文串长度分别是奇数和偶数 的情况。因为这样处理后,字符串长度就变成了奇数(如果 S 的长度为 length ,那么 T 的长度为 2 * length + 1)
2. 辅助数组 R[]
马拉车算法利用一个辅助数组 R[] 存储 回文半径,我的理解是 R[i] 表示以字符 T[i] 为中心的最长回文子串的最右字符到 T[i] 的长度(或者说,回文子串以 T[i] 为中心,T[i] 左/右边的字符数),比如以 T[i] 为中心的最长回文子串所在区间是 [l,r],那么 R[i] = r - i。所以对于 T = "#b#a#b#a#d#",R[1] = 1,详细见下表
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 字符串T | # | b | # | a | # | b | # | a | # | d | # |
| R[i] | 0 | 1 | 0 | 3 | 0 | 3 | 0 | 1 | 0 | 1 | 0 |
数组 R 有一个性质:R[i]就是在原字符串 S中,以字符 T[i]为中心的最长回文子串的长度
理由是:首先在转换得到的字符串 T 中,所有回文子串的长度都为奇数,那么对于以 T[i] 为中心的最长回文字串,其长度就为 2*R[i] + 1。由改造字符串的过程可知,对于 T 中所有的回文子串,分隔符 '#' 的数量一定比其他字符的数量多1,也就是有 R[i]+1 个分隔符,剩下 R[i] 个字符来自原字符串 S,所以对应在原字符串中的长度就为 R[i]。
有了这个性质,那么原问题就转化为求所有的 R[i]。
3. 计算 R[i]
从左往右计算数组 R[],假设 center 为之前取得最长回文子串的中心位置,right 是最长回文子串的最右端的位置,i 是当前遍历位置,这时有 两种情形:
(1)i <= right
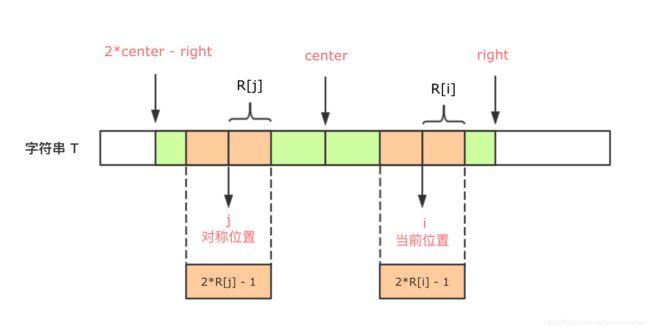
找到 i 相对于 center 的对称位置,设为 j。计算 R[i] 时,R[j](0 <= j < i) 已经计算完毕。
- 如果
R[j] < right-i,如下图:
说明以 j 为中心的回文串一定在以 center 为中心的回文串的内部,且 j 和 i 关于位置 center 对称,由回文串的定义可知,一个回文串反过来还是一个回文串,所以以 i 为中心的回文串的长度 至少 和以 j 为中心的回文串一样,即 R[i] >= R[j]。又因为 R[j] < right-i,所以 i+R[j] < right。由对称性可知 R[i] = R[j]。
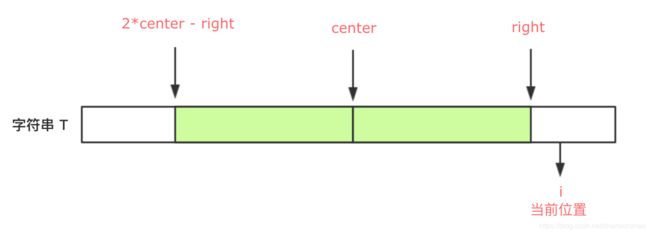
- 如果
R[j] >= right-i,如下图:
由对称性,说明以 i 为中心的回文串可能会延伸到 right 之外,而大于 right 的部分我们还没有进行匹配,所以要从 right+1 位置开始一个一个进行匹配,直到发生不匹配,从而更新 right 和对应的 center 以及 R[i]。
(2)i > right
如果 i 大于 right,说明以中心为 i 的最长回文子串还没有匹配,这个时候,就只能老老实实地一个一个匹配了,匹配完成后要更新 right 的位置和对应的 center 以及 R[i]。
注意: 为了避免更新 right 的时候出现越界错误,我们在字符串 T 的首部和尾部各增加一个与 '#' 不同的特殊字符,比如在首部添加 '@',在尾部添加 '$'。
public String longestPalindrome(String s) {
/**
字符串处理,例如 S = "babad",处理后 T = "@#b#a#b#a#d#$"
要在每个字符之间以及字符串首部和尾部添加'#',
T 的长度变为2*s.length()+1,另外又要添加'@'和'$'防止越界,
因此最终 T 的长度为2*s.length()+3
**/
char[] T = new char[2*s.length()+3];
T[0]='@'; // 避免越左边界,因为'@'肯定和右边的字符不一样,
// 匹配到'@'循环终止
T[1]='#';
T[T.length-1]='$'; // 避免越右边界,因为'$'肯定和左边的字符不一样,
//匹配到'$'循环终止
int t = 2; // 在首部添加特殊字符后,从下标 2 开始
for(char c : s.toCharArray()){
T[t++]=c;
T[t++]='#';
}
// maxLen 记录 T 中最长回文子串的长度,maxCenter为最长回文子串的中心
int maxLen=0, maxCenter=0;
// center为上一个最长回文串的中心,right为其最右端字符的位置
int[] R = new int[T.length];
int center = 0, right = 0;
// Manacher's algorithm
for (int i = 1; i < R.length - 1; ++i) {
//算法核心部分
if (i < right)
R[i] = Math.min(right - i, R[2 * center - i]);
// 从T[i]依次向两边匹配
while (T[i + R[i] + 1] == T[i - R[i] - 1])
R[i]++;
// 更新回文串中心和最右端位置
if (i + R[i] > right) {
center = i;
right = i + R[i];
}
// 如果出现更长的回文子串,更新 maxLen 和 maxCenter
if(maxLen < R[i]){
maxLen = R[i];
maxCenter = i;
}
}
// 计算最长回文子串在S中的起始位置
int index = (maxCenter - 1 - maxLen) / 2;
//返回S中的最长回文子串
return s.substring(index, index + maxLen);
}
求字符串 S 的回文子串数量
例如,字符串 "abc" 的回文子串有 "a","b","c",因此返回 3。这个问题求解依然可以使用马拉车算法,只是将寻找最长回文子串的部分换成计算回文子串数目:
public int countSubstrings(String s) {
char[] T = new char[2*s.length()+3];
T[0]='@';
T[1]='#';
T[T.length-1]='$';
int t = 2;
for(char c : s.toCharArray()){
T[t++]=c;
T[t++]='#';
}
int[] R = new int[T.length];
int center = 0, right = 0;
// Manacher's algorithm
for (int i = 1; i < R.length - 1; ++i) {
if (i < right)
R[i] = Math.min(right - i, R[2 * center - i]);
while (T[i + R[i] + 1] == T[i - R[i] - 1])
R[i]++;
if (i + R[i] > right) {
center = i;
right = i + R[i];
}
}
// 统计回文子串数目部分
int ans = 0;
for(int i : R){
ans += (i+1)/2;
}
return ans;
}
以 T[i] 为中心,能构成的回文子串长度分别为 1,3,5,... ,2*R[i]+1。
- 如果
T[i]是特殊字符'#',那么上述回文子串去掉特殊字符'#'后,在S中对应长度为2,4,6,... ,R[i],设回文子串数目是n,则有2 * n = R[i],于是n = R[i]/2; - 如果
T[i]不是特殊字符,那么上述回文子串去掉特殊字符'#'后,在S中对应长度为1,3,5,... ,R[i],设回文子串数目是n,则有2*n - 1 = R[i],于是n = (R[i]+1)/2
两者合并起来就是 n = (R[i]+1) / 2
参考资料
- [译+改]最长回文子串(Longest Palindromic Substring) Part II
- Manacher算法总结
- Manacher’s Algorithm ----马拉车算法