单应性矩阵计算(相机标定)时点的提取
前言:
本文解决问题:
1、在相机标定,也就是图像矫正过程中,参考点的选取;
2、根据选择出的点,如何计算变换矩阵,两种,调用库函数和解方程的方法
一、角点检测
cv::goodFeaturesToTrack() 检测整个图像内的角点 本例子里面无法使用。
参考:https://blog.csdn.net/guduruyu/article/details/69537083
运行后的结果如图所示:
使用findChessboardCorners() 自动寻找板内的角点
//! finds checkerboard pattern of the specified size in the image
CV_EXPORTS_W bool findChessboardCorners(
InputArray image, Size patternSize,
OutputArray corners,
int flags=CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORMALIZE_IMAGE );
第一个参数Image,传入拍摄的棋盘图Mat图像,必须是8位的灰度或者彩色图像;
第二个参数patternSize,每个棋盘图上内角点的行列数,一般情况下,行列数不要相同,便于后续标定程序识别标定板的方向;
第三个参数corners,用于存储检测到的内角点图像坐标位置,一般用元素是Point2f的向量来表示:vector
第四个参数flage:用于定义棋盘图上内角点查找的不同处理方式,有默认值。
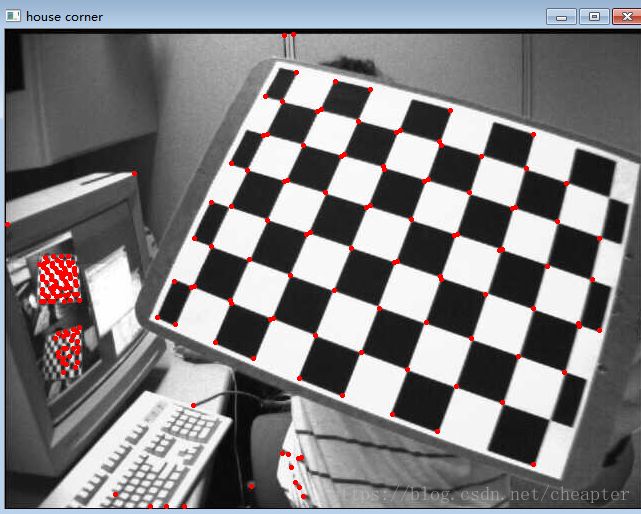
用这个函数检测,运行后结果如图:
二、根据两幅图像找到对应点
做法同上一步,对两幅图像进行同样的操作,之后可以得到两幅图中一一对应的点,这样坐标就找到了,然后就可以进行H阵的计算。只需要在corners中取相应位置的点即可。如图,取绿色的四个点,然后依据这四个点进行计算。
对两幅图处理,结果如图:
好了,点找到了,方程根据上一篇也有了,接下来就可以进行H矩阵的求取了
三、H阵的求取
可以直接使用库函数findHomography,库里定义如下:
CV_EXPORTS_W Mat findHomography( InputArray srcPoints, InputArray dstPoints,
int method = 0, double ransacReprojThreshold = 3,
OutputArray mask=noArray(), const int maxIters = 2000,
const double confidence = 0.995);使用的时候只需要设置输入输出两个地址即可,各参数意义:
1、srcPoints,dstPoints为CV_32FC2或者vector
2、ethod:0表示使用所有点的常规方法;CV_RANSAC 基于RANSAC鲁棒性的方法;CV_LMEDS 最小中值鲁棒性方法
3、ransacReprojThreshod 仅在RANSAC方法中使用,一个点对被认为是内层围值(非异常值)所允许的最大投影误差。
4、status,可选的输出掩码,用在CV_RANSAC或者CV_LMEDS方法中。注意输入掩码将被忽略。
四、工程代码
#include "opencv2/core/core.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/calib3d/calib3d.hpp"
#include "opencv2/highgui/highgui.hpp"
#include
using namespace cv;
using namespace std;
int main( int argc, char** argv ) {
Mat img1 = imread( "left3.jpg"); if( img1.empty() ) return -1;
Mat img2 = imread("left4.jpg"); if( img2.empty() ) return -1;
//将图像化为灰度图像,并且可以将起放进const数组
cv::Mat image_gray1;
cvtColor(img1, image_gray1, cv::COLOR_BGR2GRAY);
cv::Mat image_gray2;
cvtColor(img2, image_gray2, cv::COLOR_BGR2GRAY);
////设置角点检测参数
std::vector corners1; //保存检测到的点
Size board_size1 = Size(6,9); //板上的内角点行列数
std::vector corners2;
Size board_size2 = Size(6,9);
////角点检测
findChessboardCorners(image_gray1,board_size1,corners1);
findChessboardCorners(image_gray2,board_size2,corners2);
//将检测到的角点绘制到原图上
printf("使用到的四个对应点的坐标分别为: \n");
for (int i = 0; i < corners2.size(); i++)
{
if(i==2 || i==4 || i==20 || i==22) { //取四个点,采用这四个点对H阵进行求解
cout << "corners1 points is:" << corners1[i] << endl;
cout << "corners2 points is:" << corners2[i] << endl;
cv::circle(img1, corners1[i], 1, cv::Scalar(0, 255, 127), 2, 8, 0);
cv::circle(img2, corners2[i], 1, cv::Scalar(0, 255, 127), 2, 8, 0);
}
else{
cv::circle(img1, corners1[i], 1, cv::Scalar(0, 0, 255), 2, 8, 0);
cv::circle(img2, corners2[i], 1, cv::Scalar(0, 0, 255), 2, 8, 0);
}
}
printf("\n \n");
cv::imshow("校正前", img1);
cv::imshow("正视图", img2);
vector pts_src; //校正前图片中的矫正点的位置存放处
pts_src.push_back(Point2f(corners1[2].x, corners1[2].y));
pts_src.push_back(Point2f(corners1[4].x, corners1[4].y));
pts_src.push_back(Point2f(corners1[20].x, corners1[20].y));
pts_src.push_back(Point2f(corners1[22].x, corners1[22].y));
vector pts_dst; //标准图片中的矫正点位置存放处
pts_dst.push_back(Point2f(corners2[2].x, corners2[2].y));
pts_dst.push_back(Point2f(corners2[4].x, corners2[4].y));
pts_dst.push_back(Point2f(corners2[20].x, corners2[20].y));
pts_dst.push_back(Point2f(corners2[22].x, corners2[22].y));
Mat h = findHomography(pts_src, pts_dst);
cout << "单映射矩阵H为: \n" <
当然不使用库函数寻找H,自己解方程也可以得到H。方法、、、、方法正在寻找中,,,
五、解方程
网上搜到了一大堆解方程的函数,对比了,发现了区别。
首先是:cvSlove()
nt cvSolve( const CvArr* src1, const CvArr* src2, CvArr* dst, int method=CV_LU );
src1
输入矩阵
src2
线性系统的右部
dst
输出解答
method
解决方法(矩阵求逆) :
CV_LU - 最佳主元选取的高斯消除法
CV_SVD - 奇异值分解法 (SVD)
CV_SVD_SYM - 对正定对称矩阵的 SVD 方法
函数 cvSolve 解决线性系统或者最小二乘法问题 (后者用 SVD 方法可以解决):
在使用的时候发现,得到的解总是0;最后发现cvslove只能解非奇异的方程组,而且对于方程右端非零的课解,因为本例子中不是方阵,所以肯定非奇异。不能使用这个函数解方程了。
接着看说明文档,发现可以使用SVD::sloveZ()
这个函数就简单了,只需要两个参数,一个是系数矩阵A,另外一个就是解x,只能解Ax=0型的方程,不过这就够了。
所以首先把系数矩阵A给构造出来,这里采用数组给矩阵赋值的方法。代码如下:
//定义数组,方便给Mat A赋值;
float a[72] = {0};
a[l+0]=corners1[k].x; a[l+1]=corners1[k].y; a[l+2] =1; a[l+3]=0;a[l+4]=0;a[l+5]=0; a[l+6]=-1*corners2[k].x*corners1[k].x; a[l+7]=-1*corners2[k].x*corners1[k].y; a[l+8]=-1*corners2[k].x;
a[l+9]=0;a[l+10]=0;a[l+11]=0; a[l+12]=corners1[k].x; a[l+13]=corners1[k].y; a[l+14] =1; a[l+15]=-1*corners2[k].y*corners1[k].x;a[l+16]=-1*corners2[k].y*corners1[k].y; a[l+17]=-1*corners2[k].y;
l=18;k=4;
a[l+0]=corners1[k].x; a[l+1]=corners1[k].y; a[l+2] =1; a[l+3]=0;a[l+4]=0;a[l+5]=0; a[l+6]=-1*corners2[k].x*corners1[k].x; a[l+7]=-1*corners2[k].x*corners1[k].y; a[l+8]=-1*corners2[k].x;
a[l+9]=0;a[l+10]=0;a[l+11]=0; a[l+12]=corners1[k].x; a[l+13]=corners1[k].y; a[l+14] =1; a[l+15]=-1*corners2[k].y*corners1[k].x;a[l+16]=-1*corners2[k].y*corners1[k].y; a[l+17]=-1*corners2[k].y;
l=36;k=20;
a[l+0]=corners1[k].x; a[l+1]=corners1[k].y; a[l+2] =1; a[l+3]=0;a[l+4]=0;a[l+5]=0; a[l+6]=-1*corners2[k].x*corners1[k].x; a[l+7]=-1*corners2[k].x*corners1[k].y; a[l+8]=-1*corners2[k].x;
a[l+9]=0;a[l+10]=0;a[l+11]=0; a[l+12]=corners1[k].x; a[l+13]=corners1[k].y; a[l+14] =1; a[l+15]=-1*corners2[k].y*corners1[k].x;a[l+16]=-1*corners2[k].y*corners1[k].y; a[l+17]=-1*corners2[k].y;
l=54;k=22;
a[l+0]=corners1[k].x; a[l+1]=corners1[k].y; a[l+2] =1; a[l+3]=0;a[l+4]=0;a[l+5]=0; a[l+6]=-1*corners2[k].x*corners1[k].x; a[l+7]=-1*corners2[k].x*corners1[k].y; a[l+8]=-1*corners2[k].x;
a[l+9]=0;a[l+10]=0;a[l+11]=0; a[l+12]=corners1[k].x; a[l+13]=corners1[k].y; a[l+14] =1; a[l+15]=-1*corners2[k].y*corners1[k].x;a[l+16]=-1*corners2[k].y*corners1[k].y; a[l+17]=-1*corners2[k].y;
Mat A(Size(9,8),CV_32FC1,a); // 单通道
Mat H = (Mat_(8, 1) <<0,0,0,0,0,0,0,0);
//cvSolve(&A, &B, H, CV_SVD );
SVD::solveZ(A,H);
cout<< "A is \n \n" << A <(0,0),H.at(1,0),H.at(2,0)
,H.at(3,0),H.at(4,0),H.at(5,0)
,H.at(6,0),H.at(7,0),1};
Mat h(Size(3,3),CV_32FC1,h_data);
总结:不同类型数据,矩阵与数组以及图像之间的相互转化要好好掌握;
想实现某一个功能的话,首先到网上搜索下,看看库里是否有对应的函数。