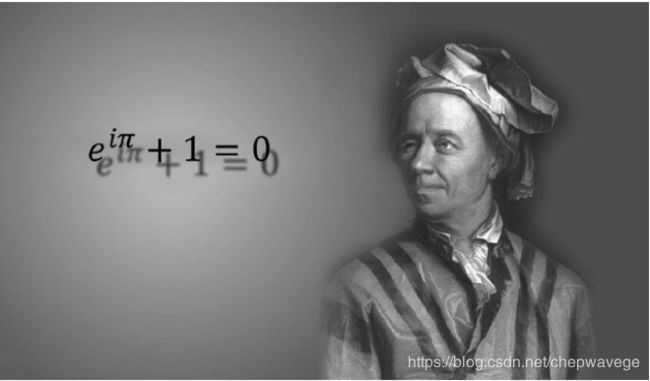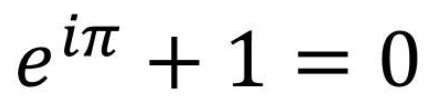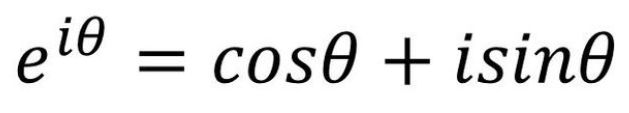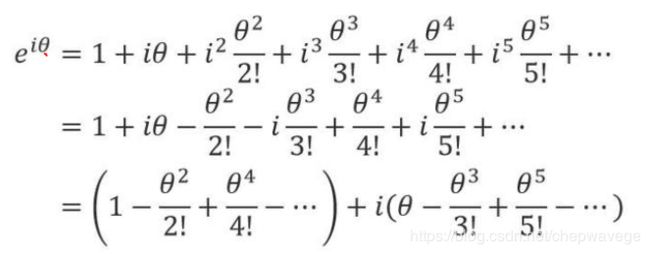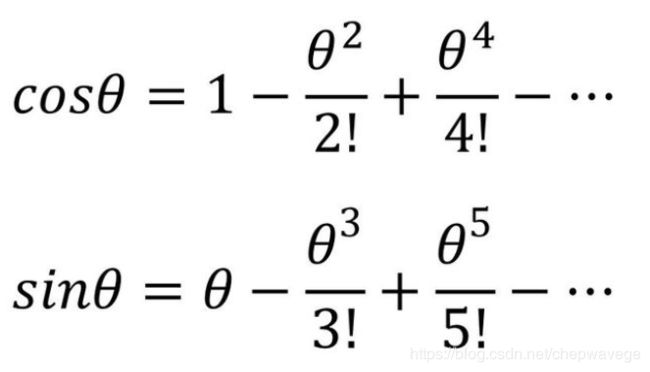欧拉恒等式:数学史上的真正完美公式!
莱昂哈德·欧拉是18世纪最伟大的数学家之一,也是人类历史上最杰出的数学家之一。作为一个多产的数学家,欧拉贡献不可估量,他提出了许多对现代数学不可或缺的概念。
在欧拉的一生中,它出版了885份关于关于数学和其他学科的论文和书籍。即使是后来失明了,他仍然笔耕不辍。欧拉在失明之后还打趣地说:“现在我就更不会分心了。” 以勤奋著称的欧拉,用他那惊人的记忆和心算能力弥补了视力的丧失。在欧拉一生丰硕的成果中,有一个以他名字命名的公式被誉为“上帝创造的公式”,那就是欧拉恒等式。
欧拉恒等式
这个公式以一种极其简单的方式将数学上不同的分支联系起来,其中涵盖了数学中最重要的几个常数,这个公式堪称是最美的数学公式。
(1)其中“e”是自然常数或者欧拉数,这是在微积分中广泛运用的自然对数的底数。这是一个无理数,也是一个超越数,它的值为2.71828……。
(2)“i”是一个复数或者是虚数单位,也是-1的平方根或者方程“x^2+1=0”的解。虚数在电子工程中极为重要,并且也在量子力学中得到应用。
(3)“π”是圆周率,这个常数不需要任何进一步的介绍,因为这是世人皆知的数学常数,在欧氏几何学和广义相对论中无处不在。
(4)自然数“1”, 任何数与之相乘都是本身。
(5)自然数“0”, 任何数与之相加都是本身。
由《物理世界》(Physics World)发起的一项调查表明,人们把欧拉恒等式与麦克斯韦方程组一起并称为“史上最伟大的公式”。物理大师费曼也盛赞这个公式为“数学最非凡的公式”。那么,欧拉恒等式是如何推导出来的呢?
证明
事实上,欧拉恒等式如下欧拉公式的一种特殊情况:
只要令θ=π,就能直接得到欧拉恒等式。那么,上述的欧拉公式又是怎么来的呢?
这个公式可以通过对e^(iθ)进行泰勒展开得到: i 作为常系数
再根据三角函数的泰勒展开:
从而可以得到欧拉公式:
当θ=π时,这个公式就能转变为我们所熟知的欧拉恒等式
用途:1. 把对应的三角形式复数 表示 指数形式的复数 (桥梁!)。目的,是可以化简复数的运算。乘除法转换成了加减法。
---》( 傅里叶变化中,傅里叶变换就是傅氏级数就是信号分解,将复杂信号分解简单的正交余弦信号,傅立叶变换得到各个信号分量的幅度与起振角度,引入欧拉公式变成复数是为了表示方便,后面对信号做运算也简单了很多,比如时域卷积经过傅立叶变换到频域就是相乘)
复数